如何实现快速位翻转总结(各种算法+方法+代码)包含雷德算法

如何实现快速位翻转总结(各种算法+方法+代码)包含雷德算法4

---

• https://blog.csdn.net/qq_42820594/article/details/98034003

先贴个有点这个图：

一、查表法

unsigned char ReverseByte(unsigned char value)
{

	static unsigned char code ReverseByteTable[256] = 
	{
	0  ,128,64 ,192,32 ,160,96 ,224,16 ,144,80 ,208,48 ,176,112,240,
	8  ,136,72 ,200,40 ,168,104,232,24 ,152,88 ,216,56 ,184,120,248,
	4  ,132,68 ,196,36 ,164,100,228,20 ,148,84 ,212,52 ,180,116,244,
	12 ,140,76 ,204,44 ,172,108,236,28 ,156,92 ,220,60 ,188,124,252,
	2  ,130,66 ,194,34 ,162,98 ,226,18 ,146,82 ,210,50 ,178,114,242,
	10 ,138,74 ,202,42 ,170,106,234,26 ,154,90 ,218,58 ,186,122,250,
	6  ,134,70 ,198,38 ,166,102,230,22 ,150,86 ,214,54 ,182,118,246,
	14 ,142,78 ,206,46 ,174,110,238,30 ,158,94 ,222,62 ,190,126,254,
	1  ,129,65 ,193,33 ,161,97 ,225,17 ,145,81 ,209,49 ,177,113,241,
	9  ,137,73 ,201,41 ,169,105,233,25 ,153,89 ,217,57 ,185,121,249,
	5  ,133,69 ,197,37 ,165,101,229,21 ,149,85 ,213,53 ,181,117,245,
	13 ,141,77 ,205,45 ,173,109,237,29 ,157,93 ,221,61 ,189,125,253,
	3  ,131,67 ,195,35 ,163,99 ,227,19 ,147,83 ,211,51 ,179,115,243,
	11 ,139,75 ,203,43 ,171,107,235,27 ,155,91 ,219,59 ,187,123,251,
	7  ,135,71 ,199,39 ,167,103,231,23 ,151,87 ,215,55 ,183,119,247,
	15 ,143,79 ,207,47 ,175,111,239,31 ,159,95 ,223,63 ,191,127,255,
	};//定义一个映射
	
	return ReverseByteTable[value];//下标对应输入值，对应元素就是输出。
}

（也可以分两次做，每次4位元，用16查表法。）
a

二、端口翻转法

阔气点的话，空出16个IO口(2组)，一个接输入，另一个接输出。

（我看有人说，果用的是CortexM3处理器，有一条REV指令，没用过不知道，可以自己查查；还有说汇编有一条有半字交换指令SWAP A，可以把累加器A中的低四位与高四位交换。）

三、蝶形变换

unsigned char ReverseByte(unsigned char dat)
{
	unsigned char ret;
	ret=dat;
	ret=(ret>>4)|(ret<<4);
	ret=((ret&0xcc)>>2)|((ret&0x33)<<2);
	ret=((ret&0xaa)>>1)|((ret&0x55)<<1);
	return ret;
}

四、不知道什么的

不是我写的，我在网上搜集的
可以扩展到任意位数。
查表法在16/32位时就太站空间了
其实有点像信号与系统里面的FFT蝶形变换，可以从最小到最大位数开始交换，也可以从最大位数到最小位数交换。

0xA : B1010
0x5 : B0101
0xC : B1100
0x3 : B0011
0xF0 : B1111 0000
0x0F : B0000 1111
Iterate from long to short
eg. 8 bit reverse.
abcd efgh -> efgh abcd -> ghef cdab -> hgfe dcba
1.
abcd efgh -> efgh abcd
2.
ef00 ab00 -> 00ef 00ab
00gh 00cd -> gh00 cd00
3.
g0e0 c0a0 -> 0g0e 0c0a
0h0f 0d0b -> h0f0 d0b0

or iterate from short to long
eg. 8 bit reverse.
abcd efgh -> badc fehg -> dcba hgfe -> hgfe dcba

unsigned char ReBit8(unsigned char x)
{
    x = ((x >> 4) & 0x0F) | ((x << 4) & 0xF0);
    x = ((x >> 2) & 0x33) | ((x << 2) & 0xCC);
    x = ((x >> 1) & 0x55) | ((x << 1) & 0xAA);
    return x;
}
//这里是因为keil for 51的编译器认为int是16位的
//如果是stm32或者是GCC编译器那么int是32位的，32和64位下的C99编译器都是这样的
inline unsigned int ReBit16(unsigned int x)
{
    return ((unsigned int)ReBit8(x)<<8) | ReBit8((x>>8));
}

inline unsigned long ReBit32(unsigned long x)        
{
    return ((unsigned long)ReBit16(x)<<16) | ReBit16((x>>16));
}

五、FFT倒序算法-雷德算法

快速傅里叶变换中用到的倒位序算法。
下面假如使用A[I]存的是顺序位序，而B[J]存的是倒位序。I<J的时候需要变序，I>J的时候就不用，不然就白忙活了。
例如：N = 8 的时候，（红色标注表示要变序）

---

倒位序	顺序	(二进制表示)倒位序	顺序
0	0	000	000
4	1	100	001
2	2	010	010
6	3	110	011
1	4	001	100
5	5	101	101
3	6	011	110
7	7	111	111

由上面的表可以看出:

按自然顺序排列的二进制数，其下面一个数总是比其上面一个数大1，即下面一个数是上面一个数在最低位加1并向高位进位而得到的。

而倒位序二进制数的下面一个数是上面一个数在最高位加1并由高位向低位进位而得到。

I、J都是从0开始，若已知某个倒位序数J，要求下一个倒位序数，则应先判断J的最高位是否为0，这可与k=N/2相比较，因为N/2总是等于100(B)的。

k=N/2

如果k>J		//这表明J的最高位为0
	只要把该位变为1（J与k=N/2相加即可），
	就得到下一个倒位序数；
如果K<=J		//这表明J的最高位为1
	可将最高位变为0（J与k=N/2相减即可）。
	然后还需判断次高位，这可与k=N\4相比较，
	如果次高位为0
		则需将它变为1（加N\4即可）其他位不变，
			既得到下一个倒位序数
	如果次高位是1
		则需将它也变为0
		然后再判断下一位
	以此类推,
	直到k = 0为止。

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main(void)
{
    int array[8]={0,1,2,3,4,5,6,7};
    int i,j,k;
    int N = 8;
    int temp;
    j = 0;
 
    for(i = 0; i < N -1; i ++)
    {
        if(i < j)
        {
            temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
 
        k = N >> 1;
 
        while( k <= j)
        {
            j = j - k;
            k >>= 1;
        }
 
        j = j + k;
    }
 
    for( i = 0; i < N; i ++)
        printf("%d ",array[i]);
    printf("\n");
 
    return 0;
}


//封装一下
//函数功能：求指定位数倒位序value的下一个倒位序,size = 0xFF+1 = 2^位数 
int Rader(int value,int size)
{
	int next = 0;		//下一个倒位序
	int k = size >> 1;	//k = size / 2
	while(k > 0)
	{
		if (k>value)		//如果k>size,说明value的最高位为0
		{
			next = value + k;//下一个倒码数就是将value的最高位变成1(直接加上k)
			break;			//推出循环
		}
		else   				//否则 k<=value  说明value的最高位是1  
		{
			value -= k; 	//先将value的最高位变成0(直接减去k)
			k >>= 1;			//然后k=k/2 等待比较次高位 循环继续
		}
	}
	return next;
}

C++的封装

#include <iostream>
using namespace std;
const int N = 8;
/*函数功能：求指定位数倒位序value的下一个倒位序,size = 0xFF+1 = 2^位数 */
int Rader(int value,int size = N)
{
	int next = 0;		//下一个倒码数
	int k = size >> 1;	//k = size / 2
	while(k > 0)
	{
		if (k>value)		//如果k>size,说明value的最高位为0
		{
			next = value + k;//下一个倒码数就是将value的最高位变成1(直接加上k)
			break;			//推出循环
		}
		else   				//否则 k<=value  说明value的最高位是1  
		{
			value -= k; 	//先将value的最高位变成0(直接减去k)
			k >>= 1;			//然后k=k/2 等待比较次高位 循环继续
		}
	}
	return next;
}



//函数功能：对顺序数组进行二进制码倒序排列
template <typename T>	
static void array_rader(T array[], int bitLen)
{
	if (NULL == array || bitLen<=0)
	{
		return;
	}
	for (int i = 1; i < bitLen;++i)
	{
		*(array + i) = Rader(*(array + i-1));
	}
}

六、一个不动脑子的算法

就是不断交换对应高位和低位

int reverseBits(int value, int bitLen) //要位逆的数及总个数的二进制位数
{
	
	int i = 0, ret = 0;
	
	for(i = 0; i < bitLen; i++)
	{
		ret |= (value & 0x1) << (bitLen - 1 - i);//采用高效的移位运算
		value >>= 1;
	}
	
	return ret;
}

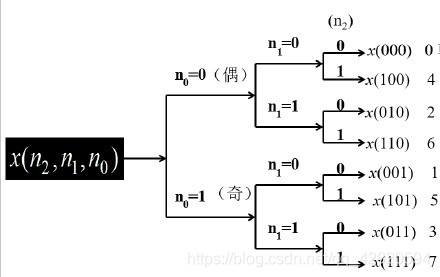
七、由奇偶分组造成的倒位序排列

以N=8为例，如下图所示：