【论文阅读】Hyperspectral Image Super-Resolution Inspired by Deep Laplacian Pyramid Network

---

论文地址

1、论文

---

受深拉普拉斯金字塔网络启发的高光谱图像超分辨率
--------金字塔去空间分辨率，然后字典对光谱分辨率…

摘要：

现有的高光谱传感器通常产生高光谱分辨率但低空间分辨率的图像，超分辨率在提高高光谱图像（HSI）的分辨率方面取得了令人瞩目的成果。然而，大多数超分辨率方法需要对同一场景进行多次观察，并在没有充分考虑光谱信息的情况下提高空间分辨率。

在本文中，我们提出了一种受深度拉普拉斯金字塔网络 (LPN) 启发的 HSI 超分辨率方法。
首先，LPN 增强了空间分辨率，它可以在不使用任何辅助观察的情况下利用自然图像的知识。 LPN 通过使用多个金字塔级别以从粗到细的方式逐步重建高空间分辨率图像。
其次，通过非负字典学习（NDL）研究了低分辨率和高分辨率 HSI 之间的光谱特性，该方法旨在学习具有非负约束的普通字典。将学习到的字典与其对应的稀疏码相乘，最终得到超分辨率结果。
在三个高光谱数据集上的实验结果证明了所提出的方法在提高 HSI 空间分辨率的同时保留光谱信息的可行性。

关键词：高光谱图像（HSI）；超分辨率；深拉普拉斯金字塔网络（LPN）；词典学习

1. 简介

高光谱成像系统通过数百个连续光谱带对场景辐射的电磁光谱进行采样。获得的高光谱图像 (HSI) [1-4] 具有高光谱分辨率，是一个数据立方体，包含从可见光到红外光谱的非常窄的光谱带，能够通过光谱特征精细表示不同的土地覆盖。因此，HSI 最近已成功应用于各种任务，例如分类 [5–7]、解混 [8–10]、去噪 [11,12] 和检测 [13–15]。然而，高光谱分辨率也是有代价的，即空间分辨率低，即获取的真实HSI数据通常提供粗糙的空间信息，因此无法捕捉到不同物体的细节。更糟糕的是，低空间分辨率会严重降低 HSI 在应用中的有效性。这强调了分辨率增强的重要性[16,17]。除了开发高分辨率传感器，一个自然的解决方案是从算法的角度进行高光谱超分辨率（需要注意的是，并非所有的高光谱数据都需要一种是从算法的角度提高空间分辨率。许多HSI（例如，基于高分辨率无人机 (UAV) 的高光谱数据）具有非常高的空间和光谱分辨率，不需要增加空间分辨率，因此不在本文的范围内。）

现有的方法大致可以分为三类。
第一类是将 HSI 与包含目标场景的高空间分辨率但低光谱分辨率图像的辅助数据源融合。广泛使用的辅助观测是全色 (PAN) 图像和多光谱图像 (MSI) [18,19]。文献中已经提出了许多基于统计的融合方法。例如，通过在贝叶斯推理框架内融合 HSI 和 PAN/MSI 来设计各种贝叶斯估计器 [20,21]。基于矩阵分解的方法在提高 HSI 的空间分辨率方面也发挥了重要作用。例如，已提出耦合非负矩阵分解 (CNMF) [22]，以将 HSI 和 PAN/MSI 交替分解为端元矩阵和丰度矩阵。已经提出了一种基于稀疏矩阵分解 [23] 的空间和光谱融合模型，以结合来自不同传感器的光谱和空间信息。此外，随着压缩感知的快速发展，稀疏表示近年来越来越受欢迎。例如，一种称为 GSOMP+ [24] 的超分辨率方法是通过将同时正交匹配追踪与解空间上的非负性约束进行推广而提出的。 [25] 开发了一种基于超像素的稀疏表示方法，以利用超像素内的相似性，而高光谱超分辨率是通过 [26] 中的字典和稀疏代码的联合估计实现的。虽然基于融合的技术可以提高 HSI 的分辨率，但它们需要在同一区域拍摄的辅助高分辨率图像，这在实践中并不总是可用。

第二类是子像素映射（SPM），它将混合像素划分为子像素并为这些子像素分配类标签。 SPM 方法由两个主要步骤组成，即通过光谱分解或软分类确定混合像素中端元的分数丰度，并通过考虑空间依赖性来评估像素内每个类的亚像素位置。已经进行了大量工作来提高涉及上述两个步骤的空间分辨率。例如，提出了一个 SPM [27] 的通用框架，以将光谱信息直接纳入空间映射过程。张等。 [28] 提出了一种基于示例的超分辨率映射模型，通过使用支持向量回归来生成高分辨率地图。在 [29] 中执行了一个集成过程，以共同解决图像融合和光谱分离问题。 [30] 中提出了亚像素分辨率专题图框架，同时提出了一种基于协作表示的 SPM 方法 [31]，以在亚像素尺度上生成改进的分类图。基于 SPM 的技术的主要局限性在于它们只能为某些应用（例如分类）获得高空间分辨率的结果。

第三类是单图像超分辨率，它从中合成具有高光谱和空间分辨率的图像低空间分辨率的 HSI 数据。单幅图像超分辨率的基本方法是传统插值法，如双线性插值法或双三次插值法。值得注意的是，深度学习 [32-35] 可以分层学习深层架构中的高级抽象表示，由于其在几个不同应用中的令人印象深刻的结果而引起了广泛的关注。最近，已经构建了许多基于深度学习的超分辨率模型。例如，在[36]中提出了一种基于深度学习的超分辨率方法来学习低分辨率图像和高分辨率图像之间的端到端映射。卷积神经网络 (CNN) [37,38] 用于学习从低分辨率 HSI 到高分辨率 HSI 的光谱差异映射，同时保留光谱信息，而 Yuan 等人。 [39] 通过将学习的 CNN 模型转移到 HSI 域并采用 CNMF 来加强低分辨率和高分辨率 HSI 之间的协作，从而利用自然图像中的知识。该类别的一个显着好处是它不需要同一场景的辅助 PAN 或 MSI 数据源。

在本文中，我们提出了一种受深度拉普拉斯金字塔网络 (LPN) 启发的单图像超分辨率框架 [40] ,41] 在保留光谱信息的情况下提高 HSI 的空间分辨率。
如图 1 所示，所提出方法的主要步骤是双重的，即空间LPN重建和非负字典学习（NDL）谱重构。
• 首先，LPN以端到端的方式使用低分辨率和高分辨率的自然图像对进行训练，而无需阶段优化。LPN由特征提取和图像重建部分组成，能够以从粗到细的方式将输入的低分辨率图像逐步上采样为重建的高分辨率图像。训练好的LPN可以直接用于提高HSI各光谱波段的空间分辨率。
• 其次，通过后续执行NDL重构光谱信息，提出学习原始低分辨率HSI与LPN得到的高分辨率HSI之间的公共字典。估计的超分辨率结果可以通过将学习的字典及其相应的稀疏代码相乘最终生成。

总而言之，这项工作的主要贡献体现在以下几点：
• 据我们所知，我们首次尝试将LPN引入HSI的超分辨率。LPN不需要在目标HSI的同一区域拍摄辅助图像，而是从轻松获取的自然图像中学习端到端映射。此外，LPN不需要任何预定义的上采样运算符（例如，双三次插值）即可将低分辨率图像放大到所需大小。
• 我们提出了一种用于光谱信息重建的NDL方法。有趣的是，光谱波段的光谱关系可以在字典学习框架内方便地表述。此外，稀疏代码和字典都被约束为非负数，这符合物理现实。

本文的其余部分组织如下：
在第2节中，我们对所提出的方法进行了详细说明。
在第3节中，报告了几个基准数据集的实验结果，以与其他方法进行比较。
结论在第4节中得出。

2. 提出的方法

在本节中，我们提供了所提出方法的详细描述，其主要步骤是LPN 的空间重建和NDL 的光谱重建。

2.1 Spatial Reconstruction by Deep Laplacian Pyramid Network

让Xl为低分辨率图像，LPN的一般架构如图2所示，从图中可以看出，用于空间重建的LPN模型由特征提取和图像重建两部分组成。

如图 2 所示，特征提取部分包含多个基本模块，这些模块包括特征嵌入子网、转置卷积层和卷积层。
特征嵌入子网络应用多个卷积层对高维非线性特征图进行变换，转置卷积层可以对输入特征进行2尺度的上采样，卷积层重构子带残差图像。值得注意的是，在第一金字塔级别增加一个卷积层，将输入的低分辨率图像转换为高维非线性特征图，而在其他金字塔级别嵌入特征则直接将前一级转置卷积层的特征转换为特征图。与其他以最高分辨率实现特征提取和重建的网络相比，LPN只需一个转置卷积层即可以更精细的分辨率生成特征图。

在图像重建部分，可以使用逐元求和将上采样图像与预测残差图像相结合，重建s级的高分辨率图像。
以低分辨率图像为输入，可以在s = log2S金字塔级别上逐步预测残差图像，其中S表示上采样比例因子，s表示金字塔级别，而上采样图像则通过使用带有转置卷积层的尺度为2的对输入图像进行上采样而获得。然后将s级的高分辨率图像作为s+1级图像重建部分的输入，整个网络由级联特征提取和图像重建子网络组成，每个层次的结构相同。
请注意，不同金字塔级别的网络共享相同的结构和任务，因此我们可以在所有级别上共享嵌入子网络、转置卷积层和卷积层的特征的网络参数。在这方面，参数数与上采样比例因子S无关，构建具有多个金字塔级别的网络需要一组参数。除了在不同级别之间共享参数外，还可以在每个金字塔级别内共享参数。更详细地说，特征嵌入子网可以通过一系列递归块来构建。图 3 描述了递归块的结构，它由 D 个不同的卷积层组成。整流线性单元 （ReLU） （R（z） = max（0， z）） 是深度学习中广泛使用的激活函数。这些卷积层的参数在递归块之间共享，因此可以在不增加参数大小的情况下有效地增加网络深度。
为了优化 LPN 中的参数 θ，我们应该定义一个适当的损失函数。LPN 的目标是学习一种映射，该映射可以生成接近高分辨率地面实况图像 Xh 的高分辨率图像 Xˆh。 让级别 s 处的残差图像为 Rˆ （s），级别 s 处的输出高分辨率图像 Xˆ（s） h 可以表述为 Xˆ（s）h = X（s）l + Rˆ （s）。通过双三次下采样将地面真实图像 Xh 在每个水平上重新调整为 Xˆ（s）h，损失函数由

其中 I 表示每批训练样本的数量，ρ（x） = √x2 + e2 表示 Charbonnier 惩罚函数 [42]，它是严格凸且无限可微的。因此，它是 l1 范数的可微变体版本。凸惩罚确保优化问题的唯一解，参数 e 确定惩罚函数与 l1 范数的相似程度。本文将e设置为1e-3，并采用随机梯度下降（SGD）求解器最小化损失函数L（θ）。训练LPN后，可以通过将HSI的每个光谱波段作为LPN的输入来确定低分辨率HSI的空间分辨率。然后将LPN的高分辨率输出堆叠到高空间分辨率HSI中，其光谱分辨率可以通过NDL重建。

2.2. 非负字典学习的光谱重建

让矩阵 Sh ∈ Rb×MN 表示高空间分辨率 HSI，将 LPN 生成的 HSI Sh，3D ∈ RM×N×b 的像素连接起来，即 Sh，3D ∈ RM×N×b → Sh ∈ Rb×MN，其中 M、N 表示空间维度，b 表示光谱波段的数量。通过假设属于同一类的像素的光谱特征近似位于相同的低维子空间中[43]，矩阵Sh可以表示为：

其中 D = [d1， d2， . . . ， dK] ∈ Rb×K 是字典，其列 {dk}k=1，2,…,K 是包含所有类的光谱特征的原子，Vh 表示未知稀疏代码。D和Vh都被约束为非负数，这与物理现实相吻合。同样，原始的低空间分辨率HSI也可以通过将原始输入HSI Sl，3D∈Rm×n×b中的像素连接起来，将原始的低空间分辨率HSI重塑为Sl∈ Rb×mn，其中m，n表示空间维度，b表示光谱波段的数量。与 sh 类似，我们也可以将 Sl 重新表述为

请注意，低分辨率和高分辨率 HSI 捕获相同的场景，并且这些数据的基础材料是相同的。因此，我们在方程（2）和（3）中共享相同的字典D。此外，字典D和Vl被限制为非负数，以掌握数据的物理性质。方程 （2） 和 （3） 中的 l0 优化问题可以近似地替换为基于 l1 的问题。结合两个基于 l1 的问题，我们有

其中 λ、β （λ ≥ 0， β ≥ 0） 是正则化参数。设 S = [Sl， βSh] 且 V = [Vl， βVh] ，公式 （4） 得到

到目前为止，光谱重建问题已经转化为等式（5）中所示的字典学习问题，可以通过在固定其他变量的情况下交替优化某个变量来解决。更详细地说，对于固定字典 D，关于 V 的子问题可以写为

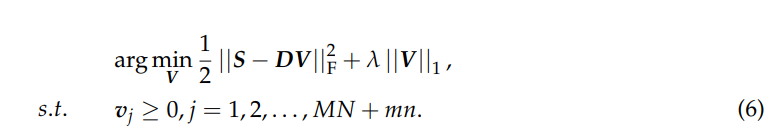
公式（6）中的上述问题可以通过乘子交替方向法（ADMM）[44]有效求解。重新制定等式（6），我们有

其增强拉格朗日函数产生

其中 μ > 0 是惩罚参数，T 表示拉格朗日乘数。
在不损失通用性的情况下，（p + 1）次迭代中的矩阵W和V可以分别由下式确定

其中 E 是单位矩阵，[·]+ = max{·， 0} 和 S λ 2μ 是收缩运算符，由下式给出

基于W（p+1）和V（p+1），拉格朗日乘数T（p+1）可以更新为下式

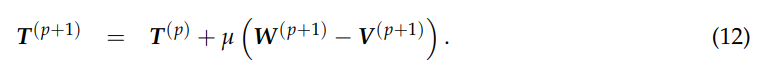
此外，我们通过修复 V 来更新 D

设 D（q） 表示在第 q 次迭代中学习的字典，d（q+1）k = d（q）k + ∆dk，方程 （13） 中的问题可以通过块坐标下降法 [45] 求解，即每次迭代中只更新 D（q） 的一列，而保持其他列固定，∆dk 可以由下式确定

其中 vk 来自矩阵 V 的第 k 行，vk，j 表示位于第 k 行和第 j 列的 V 元素，δ（q）i，j 表示位于第 i 行和第 j 列的 S − D（q）V 元素。
根据公式（14），d（q+1）k可以写成

上述更新V和D的步骤是解决公式（5）中字典学习问题所需的主要步骤，算法1总结了完整的算法。

3.实验与分析

3.1 数据集

为了评估所提出方法的性能，在三个 HSI（即 CAVE [46]、Indian Pines [47] 和 Pavia Center [1]）上进行了实验。下面对HSI数据集进行简要说明：
1、CAVE：CAVE 数据集 [48] 包含 32 个物体的 HSI，具有 512×512 空间像素和 31 个光谱带，范围从 400 到 700 nm，间隔为 10 nm 宽。实验中使用的八个测试数据的高分辨率红绿蓝 (RGB) 图像绘制在图 4.2 中。
2、Indian Pines：Indian Pines 数据集 [49] 由印第安纳州西北部农业 Indian Pine 试验场上空的机载可见光/红外成像光谱仪 (AVIRIS) 传感器捕获。原始数据集由 224 个光谱波段组成，通过去除零波段和噪声波段，将 200 个波段用于实验。实验中空间分辨率为 20 m，空间尺寸为 256×256。图5a描绘了具有丰富空间结构的Indian Pines数据集的高分辨率RGB图像。
3、Pavia Center 帕维亚中心：帕维亚中心数据集 [50] 由意大利帕维亚中心市区的反射光学系统成像光谱仪 (ROSIS-03) 光学传感器获取。原始场景包含 1096 × 715 像素和 115 个光谱波段。空间分辨率为1.3 m，空间大小为128×128的一部分包含丰富的详细信息，是从原始数据集中选择的。去除 13 个非信息通道后，剩下 102 个波段用于实验。高分辨率 RGB 图像如图 5b 所示。

3.2 实验设置

我们将所提出的方法与几种众所周知的方法进行了比较，即双三次，[51] 提出的基于稀疏编码的方法（称为 Zeyde），锚定邻域回归（ANR）[52]，最小二乘邻域嵌入（ NE + LS），具有非负最小二乘法的邻域嵌入（NE + NNLS）[53]，具有局部线性嵌入的邻域嵌入（NE + LLE）[54]，A+ [55]，超分辨率 CNN（SRCNN）[ 36]、CNMF [22]、引导滤波器主成分分析（GFPCA）[56]、Gram-Schmidt 光谱锐化（GS）[57]、自适应 GS（GSA）[58]，以及提出的高光谱超分辨率方法[59]（称为 HySure）。为了符号方便，我们基于 LPN 和 NDL 的方法缩写为 LPN-NDL。双三次方法是一种基于多项式的插值方法。 Zeyde 是一种基于稀疏表示和字典学习的有效方法。 ANR 使用岭回归来学习范例邻域，可用于计算低分辨率和高分辨率块之间的映射。 NE + LS、NE + NNLS 和 NE + LLE 是具有不同约束的邻居嵌入方法。 A+ 结合了 ANR 的优点和简单的功能，是 ANR 的改进版本。 SRCNN 通过应用深度 CNN 学习低分辨率图像和高分辨率图像之间的端到端映射。 CNMF通过交替分解低空间分辨率HSI和相应的高空间分辨率辅助数据来获得高空间分辨率HSI。 GFPCA 是一种混合高光谱全色锐化方法，通过结合引导滤波器和 PCA 实现。 GS通过对不同的低空间分辨率波段进行Gram-Schmidt变换来重建高空间分辨率图像，GSA是GA的自适应变体。 HySure 将超分辨率问题表述为凸规划，通过分裂增广拉格朗日收缩算法 (SALSA) 求解。此外，bicubic、Zeyde、ANR、NE + LS、NE + NNLS、NE + LLE、A+、SRCNN 和 LPN-NDL 方法是使用低分辨率 HSI 执行超分辨率的单图像方法，而 CNMF、 GFPCA、GS、GSA 和 HySure 方法是基于辅助的方法，需要同一场景的辅助 PAN 或 MSI 数据源。请注意，真实的 PAN 在实践中是不可用的，因此我们从真实的高分辨率 HSI 生成 PAN 作为真实 PAN 的替代品。更详细地说，可见光谱带的平均值用作高光谱数据的 PAN [16]。通过使用标准偏差设置为 1 的高斯核然后向下模糊原始 HSI 来模拟低分辨率 HSI -使用比例因子 S = 2、4 或 8 对模糊的 HSI 进行采样。竞争方法中的参数按照其相应参考文献中的描述进行选择。 LPN-NDL 的详情如下。在空间重建步骤中，我们使用多个低分辨率和高分辨率自然图像对以端到端的方式训练 LPN。训练数据由来自 [60] 的 91 张图像和来自 Berkeley 分割数据集 [61] 的 200 张图像组成。 LPN 不是输入通过预处理获得的放大图像，而是直接获取低分辨率图像并逐步重建不同金字塔级别的高分辨率图像。 LPN 由 s = log2 S 子网络组成，用于超分辨率低分辨率比例因子 S 的图像。例如，在 S = 4 的情况下，LPN 有 s = 2 个子网络。我们可以根据经验设置方法的参数以达到可接受的性能。卷积/转置卷积滤波器的滤波器大小可以设置在 3 到 9 的范围内，一个块和递归块中的卷积层数可以分别设置为大于 2 和 4。初始学习率可以设置为低于 0.001 和高于 10−6。具体来说，在本文中，LPN 的每个卷积层包含 64 个大小为 3×3 的滤波器，而转置卷积滤波器的大小为 4×4。非线性激活函数是泄漏整流线性单元（LReLUs）负斜率 0.2，所有卷积层和转置卷积层后跟 LReLU。批量大小和训练时期分别设置为 64 和 1000。块中的卷积层数和递归块的数量分别设置为 5 和 8。采用 SGD 求解器训练网络，学习率初始化为 5×10−6，每 100 个 epoch 减少 2 倍。在光谱重建步骤中，NDL 中的参数 λ、β 和 μ 分别选择为 0.001、5 和 0.005。此外，实验是在 Intel® Xeon® CPU E5- 上使用 MATLAB 2018a 进行的。 2620 V4 平台 (2.10 GHz)，64 GB 内存，运行 Microsoft Windows 7 操作系统。 LPN-NDL 在三个 HSI 数据集上的执行时间分别约为 290 秒、280 秒和 40 秒。

3.3. 评价指标

对竞争方法进行定量评估采用6个评价指标：（1）均方根误差（RMSE）[62];（2）峰值信噪比[63];（3）结构相似性指数[64];（4）相对全球合成的维度错误[63，65];（5）光谱角度映射仪（SAM）[66]和（6）各向异性质量指数（AQI）[67]。设 Y ∈ Rb×MN 表示具有 b 波段和 MN 像素的参考高分辨率图像，Y=[y1，·，y2，·,…,yb，·]T =[y·，1，y·，2,…,y·，MN]，whereyi，·∈RMN×1isfromtheith（i=1，2,…,b）带和y·，j ∈ Rb×1是第j个（j = 1， 2， . . . ， MN）像素的特征向量。假设 Yˆ ∈ Rb×MN 给出了估计的高分辨率图像，下面给出了每个索引的详细信息。

3.3.1. RMSE

RMSE [62] 是参考 Y 对预测 Yˆ 值的扩散的度量，它由以下均方误差的平方根获得

RMSE 越小，表明估计的 Yˆ 更接近参考数据。

3.3.2. PSNR

PSNR [63] 是信号的最大功率与残差功率之间的比率。第i个波段的PSNR由

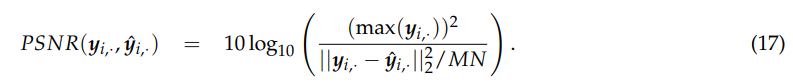
PSNR值越大，表示超分辨率的质量越高。由于 HSI 的 b > 1，因此所有波段的平均 PSNR 用于表示整个图像的质量指数.

3.3.3.SSIM

SSIM [64]基于人类视觉感知，它对参考数据的结构一致性很敏感。第 i 个波段的 SSIM 定义为

其中 μ ̃yi，·和 μ ̃yˆi，· 表示 yi 的平均值，·和 yˆi，·，分别是 σ2yi，·， σ2yˆi，·和 σyi，·yˆi，·是 yi，·， yˆi，· 的方差和彝的协方差，·yˆi，· 和 c1 和 c2 是两个常数，用于用弱分母稳定除法。当 SSIM 较大时，估计的图像 Yˆ 更接近参考数据。由于 HSI 中有数百个波段，因此所有波段的平均 SSIM 用于表示整个影像的质量指数。

3.3.4 ERGAS

ERGAS [63，65] 是超分辨率质量的全局统计度量，最佳值为 0。Y 和 Yˆ 的 ERGAS 计算公式为

其中μ ̃yi 的含义与公式 （18） 中的含义相同。

3.3.5. SAM

SAM [66] 评估每个像素的光谱信息保存情况。第 j 个像素处的 SAM 由下式确定

较小的 SAM 意味着估计的 HSI 更接近参考 HSI，SAM 的最佳值为 0。所有 MN 像素的平均 SAM 用作整个图像的质量指数。

3.3.6. AQI

AQI [67] 是一种无参考质量指标，不需要任何真实图像来确定图像的质量。该指数基于在一组预定义方向上测量图像的各向异性。第 i 个波段的 AQI 可以由下式建模

其中 θr 表示用于测量熵的 rth （r = 1， 2， . . . ， R） 方向，H（i， θr） 是第 i 个波段的熵的期望值，μi 表示 H（i， θr） 的平均值。AQI 越小，表示图像质量越高。所有波段的平均AQI用于表示整个影像的质量指数。

3.4.实验结果

3.4.1．与最先进方法的比较

上述方法的定性和定量结果分别如图 6-10 和表 1-3 所示。表1为8个测试数据的平均结果，括号内为各评价指标在8个测试数据上的标准差。表 2 和表 3 分别比较了 Indian Pines 数据和 Pavia Center 数据的评估指标，括号中显示了通过平均计算的那些指标（即 PSNR、SSIM、SAM 和 AQI）的标准差。不失一般性，我们为所有 HSI 数据集设置比例因子 S = 4。从实验结果来看，一些观察结果值得注意。首先可以看出，与其他单图像方法相比，双三次、SRCNN 和 LPN-NDL 方法产生了更优越的性能，而与其他基于辅助的方法相比，CNMF 取得了更好或相当的结果。例如，从表 1-3 可以看出，双三次、SRCNN 和 LPN-NDL 方法总是提供比 th 更低的 RMSE 和更高的 PSNR。Zeyde，ANR，NE + LS，NE + NNLS，NE + LLE和A +方法。SSIM、ERGAS、SAM和AQI指数也提供类似的属性。此外，如表1所示，CNMF的RMSE，ERGAS和SAM远低于GFPCA，GS，GSA和Hysure，而CNMF的PSNR，SSIM和AQI高于其他辅助方法。上述现象证明了基于双立方、CNMF和深度学习的HSI超分辨率方法的有效性。

其次，在大多数情况下，所提出的 LPN-NDL 方法在所有比较方法中实现了最佳性能，而不需要同一场景的辅助 PAN 或 MSI。如表 1 所示，LPN-NDL 的 RMSE 导致最大下降 25，而 PSNR 的改善最多为 12 dB。 SSIM、SAM 和 AQI 也优于其他方法。 LPN-NDL 的 ERGAS 优于单图像方法，但与基于辅助的方法相当或略逊一筹。从图 6 中还可以清楚地看到，LPN-NDL 在所有比较方法中提供了最佳的视觉质量。具体来说，LPN-NDL 生成的“花”图像比其他方法获得的图像清晰得多。 Indian Pines 数据集和 Pavia Center 数据集的重建结果也产生了类似的属性。这意味着基于 LPN 的空间重建和基于 NDL 的光谱重建可以提高 HSI 超分辨率的性能。

第三，与竞争方法相比，LPN-NDL 提供更好或相当的光谱保真度。从表 1 中值得注意的是，LPN-NDL 的 SAM 低于其他方法。为了进一步了解，图 9 绘制了 CAVE（油画图像和照片和面部）、印度松树和帕维亚中心数据集中位于 (10,10) 的像素的光谱特征。如图 9 所示，LPN-NDL 获得的光谱轮廓与其对应的 ground-truths 接近，表明 LPN-NDL 可以有效地保留原始 HSI 的有用光谱信息。此外，可以清楚地看到图 9d 中 LPN-NDL 的结果略逊于图 9a-c 中的结果。这是因为 Pavia Center 的空间大小远小于其他两个数据集，并且 Pavia Center 数据集的低分辨率图像比其他两个数据集的图像模糊得多。图 10 描绘了不同频段的 PSNR。可以看出，当光谱波段数大于 5 时，LPN-NDL 在 CAVE 数据上的性能变得相对稳定，而 LPN-NDL 在其他两个数据集上的 PSNR 随光谱反射率而变化。例如，如图 10c 所示，强度较高的条带比强度较低的条带获得更高的误差范围。简而言之，实验结果验证了所提出的 LPN-NDL 方法在高光谱数据超分辨率方面的有效性。

3.4.2.统计显着性分析

我们使用 Kruskal-Wallis 检验通过将其结果与单图像方法和基于辅助的方法对上述数据集的 RMSE 结果进行比较来进一步研究所提出方法的统计显着性。 Kruskal–Wallis 检验是一种非参数方法，用于比较多个数据集上的多种超分辨率方法。 Kruskal-Wallis 检验考虑了上述 14 种超分辨率方法和三个 HSI 数据集（即 CAVE 中的八个测试数据、Indian Pines 和 Pavia Center 数据）。所有竞争对手都为每个数据集排名，性能最好的方法排名 1，第二好的方法排名 2，依此类推。如果这些方法在某个数据集上具有相同的性能，则所有这些方法都会获得它们的平均排名。 Kruskal–Wallis 检验的零假设是所有方法都是等价的。在本文中，p 值等于 2.35 × 10−7；因此，我们根据显着性水平 α = 0.05 拒绝原假设。为了评估这些方法之间的差异，我们随后进行了多重比较以确定在哪些水平上将一种方法与其他方法区分开来。图 11 绘制了 Kruskal–Wallis 检验的结果，以将所提出的方法与单图像方法和基于辅助的方法进行比较。从图 11a 中可以看出，LPN-NDL 的中位数和四分位数范围比竞争方法小得多，验证了所提出的 LPN-NDL 的优越性。此外，图 11b 中描述了任何两种方法之间等级差异的图形表示，这表明 LPN-NDL 与几乎所有其他方法之间存在显着差异 (p < 0.05)。基于以上分析，所提出的 LPN-NDL 方法明显优于其他方法。

3.4.3.参数的敏感性分析

这里评估关键参数的敏感性（即，上采样比例因子 S、训练时期的数量以及正则化参数 λ 和 β）。图 12 显示了比例因子 S 对 Indian Pines 和 Pavia Center 数据集的 RMSE 的影响。可以看到 RMSE 随着 S 的增加而增加。这是因为具有较大比例因子的超分辨率比具有较小比例因子的超分辨率更具挑战性。然而，这并不一定意味着最佳比例因子简单地选择为2。最佳比例因子应根据重建误差和实际应用中的实际需求来确定。训练时期数的影响如图13所示，从中可以观察到，RMSE 在前几个 epoch 增加，然后随着 epoch 数量的增加而迅速减小，然后随着 epoch 数量的增加再次缓慢减小并最终趋向于某个稳定值。如图 13 所示，建议 LPN 训练超过 400 个 epoch 以获得稳定有效的性能。最后，图 14 绘制了正则化参数 λ 和 β 的效果。 λ 选自 {10−5, 5 × 10−5, 10−4, 5 × 10−4, 0.001, 0.005, 0.01}，而 β 选自 {0.01, 0.1, 1, 5, 10}。从图14可以看出，虽然超分辨率性能随着参数的变化而波动，但变化幅度较小。此外，注意到用 λ ∈ {10−5, 5 × 10−5, 10−4, 5 × 10−4} 和 β ∈ {0.01, 10} 获得的 RMSE 比用其他范围获得的更不稳定，它最好将λ的值设置在0.001到0.01的范围内，将β的值设置在0.1到5的范围内。

4. 结论

在本文中，我们提出了一种基于深度学习的高光谱超分辨率方法，可以从低分辨率 HSI 重建高分辨率 HSI。所提出的 LPN-NDL 方法设计了一个 LPN 模型来增强空间分辨率，然后使用 NDL 方法来保留光谱信息。与大多数现有的超分辨率方法相比，所提出的 LPN-NDL 的一个显着优势是它不需要同一场景的任何辅助图像（例如，PAN 或 MSI）。此外，通过嵌入多个转置卷积层，LPN-NDL 不需要任何预处理（例如双三次插值）即可将低分辨率图像放大到所需尺寸，并且非负约束被添加到光谱重建中步骤服从物理现实。三个高光谱数据集的实验结果表明，在大多数情况下，LPN-NDL 可以提供比竞争方法更小的误差。一个可能的未来研究方向是通过进一步避免过度拟合来改进所提出的方法。如何将所提出的方法扩展到其他应用领域（例如，高光谱解混和分类）也是未来的研究课题。