物理化学笔记（1-5章）

复习参考：每一章的$ppt$总结课件,所有的作业题。所有的课堂检测题，以下重点

$第二章：化学热力学基本原理$

1：p18 系统的分类
2：对于不同系统的计算公式（重点看等温可逆，等温不可逆，可逆相变，绝热可逆过程）
3：p39 例2.6，可逆相变
等温恒外压，自由膨胀$=$等于不可逆

1根据系统的环境间的联系不同可把系统分为三类：
敞开系统：系统与环境间既有物质交换，也有能量交换
封闭系统：系统与环境之间只有能量交换，而没有物质交换
孤立系统：系统与环境之间既无物质交换也没有能量交换，也称隔离系统

2：化学热力学计算公式
基本公式：
理想气体状态方程：$PV=nRT=\frac{m}{M}RT$
热力学第一定律：$\Delta U=Q+W$
焓：定义式$H=U+pV$
热容：$C_{V,m}=2.5R,C_{P.m}=3.5R$
$Helmholtz$函数：$A\stackrel{def}{=}U-TS$
吉布斯函数：$G\stackrel{def}{=}H-TS=U=pV-TS=A+pV$
熵：$dS\stackrel{def}{=}\frac{\delta Q_r}{T},\Delta S={\int }_A^{B}dS={\int }_A^B\frac{\delta Q_r}{T}$

反应条件	$Q$	$U$	$W$	$\Delta S$	$\Delta H$	$G$	$A$
等温可逆$\Delta T=0$	$nRTln\frac{V_2}{V_1}=nRTln\frac{p_1}{p_2}$	$0$	$nRTln\frac{V_1}{V_2}=nRTln\frac{p_2}{p_1}$	$nRln\frac{V_1}{V_2}=nRln\frac{p_2}{p_1}$	$0$	$nRTln\frac{V_1}{V_2}=nRTln\frac{p_2}{p_1}$	$nRTln\frac{V_1}{V_2}=nRTln\frac{p_2}{p_1}$
等温不可逆$\Delta T=0$	$nRTln\frac{V_2}{V_1}=nRTln\frac{p_1}{p_2}$	$0$	$pdV=-{\int }_{V_1}^{V_2}pdV$	$nRln\frac{V_1}{V_2}=nRln\frac{p_2}{p_1}$	$0$	$nRTln\frac{V_1}{V_2}=nRTln\frac{p_2}{p_1}$	$nRTln\frac{V_1}{V_2}=nRTln\frac{p_2}{p_1}$
等压过程$\Delta P=0$	$n{C}_{P,m}\Delta T$	$n{C}_{V,m}\Delta T$	$-P\Delta V$	$n{C}_{P,m}ln\frac{T_2}{T_1}$	$n{C}_{P,m}\Delta T$	$略$	$略$
等容过程$\Delta V=0$	$n{C}_{V,m}\Delta T$	$n{C}_{V,m}\Delta T$	$0$	$n{C}_{V,m}ln\frac{T_2}{T_1}$	$n{C}_{P,m}\Delta T$	$略$	$略$
自由膨胀$Q=U=W=0$	$0$	$0$	$0$	$nRln\frac{V_2}{V_1}=nRln\frac{p_1}{p_2}$	$0$	$nRTln\frac{V_1}{V_2}=nRTln\frac{p_2}{p_1}$	$nRTln\frac{V_1}{V_2}=nRTln\frac{p_2}{p_1}$
绝热可逆$Q=0$	$0$	$n{C}_{V,m}\Delta T$	$n{C}_{V,m}\Delta T$	$S_r=0$	$n{C}_{P,m}\Delta T$	$0$	$0$
绝热不可逆$Q=0$	$0$	$n{C}_{V,m}\Delta T$	$n{C}_{V,m}\Delta T$	$$\begin{gathered} nRln\frac{p_1}{p_2}+n{C}_{P,m}ln\frac{T_2}{T_1} \\ nRln\frac{V_2}{V_1}+n{C}_{V,m}ln\frac{T_2}{T_1} \\ n{C}_{P,m}ln\frac{V_2}{V_1}+n{C}_{V,m}ln\frac{p_2}{p_1} \end{gathered}$$	$n{C}_{P,m}\Delta T$	$0$	$0$
可逆相变	$n{\Delta }_c{H}_m$	$-P_{ex}\Delta V$	$Q-P_{ex}\Delta V$	$\frac{n{\Delta }_{pc}{H}_m}{T}$	$n{\Delta }_{pc}{H}_m$	$0$	$-P\Delta V$
不可逆相变	$n{\Delta }_c{H}_m$	$-P_{ex}\Delta V$	$Q-P_{ex}\Delta V$	$设计过程$	$设计过程$	$\Delta H-T\Delta S$	$\Delta U-T\Delta S$

例2.6：$101kPa$下，$2mol$的$373K$的水变为同温度的水蒸气，计算此过程的$Q、W、\Delta U$和$\Delta H$
$由于在101kPa下的水的沸点为373K，故此条件为可逆过程，则$$$Q=\Delta H=n{\Delta }_{vap}{H}_m=2\times 30.7=8.14\times 10^{4}J=81.4kJ$$水的体积可忽略不计，把水蒸气看做理想气体，则$$W=-p_{ex}(V_g-V_l)\approx p{V}_g=-nRT=2\times 8.314\times 373=-6.2\times 10^{3}J=-6.20kJ$$$$U=Q+W=81.4+(-6.20)=75.2kJ$$

某容器中装有$H_2$和$N_2$,总压为$150kPa$,温度$300K$。将$N_2$分离后容器中只剩下$H_2$,压力降为$50kPa$,容器中气体质量减少$14g$。试计算:
(1)容器的体积。
(2)容器中$H_2$的质量。
(3)$N_2$分离前容器中$H_2$和$N_2$的摩尔分数。

$1mol$单原子分子理想气体，初态为$298K、202.6kPa，$绝热可逆膨胀到$187K$，计算该过程的$Q、W、\Delta U、\Delta H？$

求 $101.3kPa$ 下，将 $1mol、-10℃$的过冷水蒸发成 $10℃$水蒸气过程的 $Q、W、\Delta U$ 和$\Delta H$。水蒸气可看作理想气体。 已知：$C_p[H_{2}O(l)]＝4.184kJ\cdot K^{-1}\cdot k{g}^{-1}$，$C_p[H_{2}O(g)]＝1.74kJ\cdot K^{-1}\cdot k{g}^{-1}$。在正常沸点 （$373K$）下水的气化热为${\Delta }_{vap}{H}_m＝40.67kJ\cdot mo{l}^{-1}$，$H_{2}O$ 的摩尔质量 $18g\cdot mo{l}^{-1}$。

将$22.4$ 克氧气(可看作理想气体)在 $100kPa$ 下，由 $25℃$升温到 $50℃$，再保持 在此温度下可逆膨胀体积增大一倍，计算整个过程的 $Q、W、\Delta U$ 和$\Delta H$。

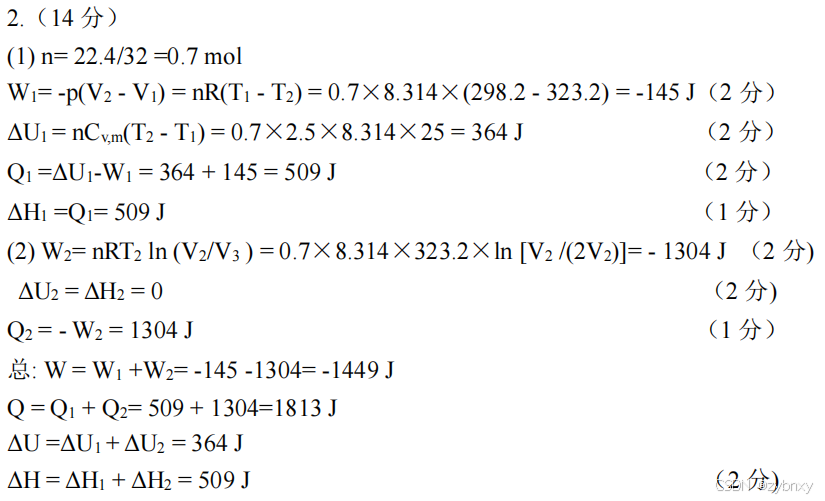
已知反应$C{H}_{3}COOH(l)＋C_{2}H5OH(l)=C{H}_{3}COO{C}_2{H}_5(l)＋H_{2}O(l)$的$(298K)＝－9.20kJ\cdot mo{l}^{-1}$。$25℃$下，$C_2{H}_{5}OH(l)$及$C{H}_{3}COOH(l)$的标准摩尔燃烧焓分别为$－1367kJ\cdot mo{l}^{-1}$和$－875kJ\cdot mo{l}^{-1}，C{O}_2(g)$和$H_{2}O(l)$的标准摩尔生成焓分别为$－394kJ\cdot mo{l}^{-1}$ 和$－286kJ\cdot mo{l}^{-1}$。计算$25℃$下$C{H}_{3}COO{C}_2{H}_5(l)$的标准摩尔生成焓。

已知某理想气体的$C_{p,m}＝29.1J\cdot mo{l}^{-1}\cdot K^{-1}$。将$5mol$此气体由始态$400K、200kPa$经下列不同的绝热过程膨胀到压力为$100kPa$：
（1）可逆。
（2）对抗恒外压$100kPa$。
分别计算这两种过程的$Q、W、\Delta U、\Delta H$和$\Delta S$。

将$1mol$苯蒸气由$80℃、40.0kPa$冷凝为$60℃、100kPa$的液体苯，求此过程的$\Delta S$。已知苯的标准沸点为$80℃$，在此条件下苯的蒸发焓为$30.9kJ\cdot mo{l}^{-1}$，液体苯的等压质量热容为$1.80J\cdot g^{-1}\cdot K^{-1}$。苯蒸气可看作理想气体。

$1mol{N}_2$气体（视为理想气体）由 $273K、101.3kPa$恒温不可逆膨胀到 $50.6kPa$，系统对外做功 $418.4J$。
（1）计算该过程的 $Q、W、\Delta U、\Delta H、\Delta S$和$\Delta G$，并判断过程的方向；
（2）若该系统由上述始态恒温可逆膨胀到上述终态，计算系统对外做功及$\Delta G$。

$1mol$ 液体苯在$353K$，$100kPa$下蒸发变为同温同压的气体苯，计算此变化过程的$Q、W、\Delta U、\Delta H、\Delta S、\Delta A$和$\Delta G$。已知苯在正常沸点$353K$时${\Delta }_{vap}{H}_m=30.75kJ.mo{l}^{-1}$，苯蒸气可视为理想气体且液体苯的体积可以忽略。

$第三章：多组分系统热力学$

1：p79 化学势判据
2：p84 稀溶液的两个经验定律（数学表达式，使用条件）
3：p89 稀溶液的依数性

1：化学式判据：等温，等压，无非体积功的情况下，物质总是自动地由化学势高的一相向化学势低的一相转移，这种相间物质的转移一直进行到该物质在两相的化学势相等时停止。各物质在各相的化学势相等是达到相平衡的条件。
系统自发过程与限度的判据为$$dG=\sum _B{\mu }_B{d}_{n_B}\le 0$$多组分多相系统的每一项都均服从上式，设其中任意一项为$\alpha$，则有：$$dG(\alpha )=\sum _B{\mu }_B(\alpha )d_{n_B}(\alpha )$$系统的$G$为各相的$G$之和，则有$$dG=\sum _{\alpha }dG(\alpha )=\sum _{\alpha }\sum _B{\mu }_B(\alpha )d_{n_B}(\alpha )$$于是得到等温，等压，无非体积功条件下的化学势判据：$$\sum _{\alpha }\sum _B{\mu }_B(\alpha )d_{n_B}(\alpha )\le 0\left(\begin{array}{c}<0自发\\ =0平衡\end{array}\right)$$
当由$\alpha$相转移到$\beta$相，则即$$\begin{gathered} \sum _{\alpha }\sum _B{\mu }_B(\alpha )d_{n_B}(\alpha )=\sum _B{\mu }_B(\alpha )d_{n_B}(\alpha )-\sum _B{\mu }_B(\beta )d_{n_B}(\beta ) \\ ={\mu }_A(\alpha )(-d_{n_A})+{\mu }_A(\beta )d_{n_A} \\ =[{\mu }_A(\beta )-{\mu }_A(\alpha )]d_{n_A}\le 0 \end{gathered}$$则可以得知$${\mu }_A(\beta )-{\mu }_A(\alpha )\le 0$$可证明上述结论。

2：拉乌尔定律：稀溶液中，溶剂的蒸气压等于同温度下纯溶剂的蒸气压与溶液中溶剂摩尔分数的乘积。即$$p_A=p_A^{\ast }{x}_A$$其中$p_A^{\ast }$为同温度下纯溶剂的饱和蒸气压$x_A$为溶液中溶剂$A$的摩尔分数。溶液越稀，按拉乌尔定律计算出的$p_A$与实际值就越吻合。

亨利定律：一定温度下，气体B的平衡分压$p_B$与它在溶液中的浓度成正比，比例系数为一常数，即$$p_B=k_x{x}_B/p_B=k_b{b}_B/p_B=k_c{c}_B$$分别为亨利定律在分压，摩尔分数，质量分数的使用方法。
在同一温度下，$k_x,k_b.k_c$之间存在一定的换算关系$$k_b=k_x{M}_A$$$$k_c=\frac{k_x{M}_A}{{\rho }_A}$$拉乌尔定律在任何时候都可以人家用，而亨利定律必须在溶质在与液体中的分子状态相同时使用，并且，在溶剂中溶入几种挥发性溶质形成稀溶液时，各组分可以分别应用亨利定律。

3：稀溶液的四个依数性：蒸气压下降，凝固点降低，沸点升高，渗透压。
依数性：稀溶液的一些性质只与加入溶质的数量有关而与溶液本性无关，被称为依数性质。稀溶液中溶剂的化学势小于纯溶剂的化学势是稀溶液产生依数性的根本原因。

蒸气压下降：稀溶液中溶剂的蒸气压低于同温度下的纯溶剂的蒸气压。
凝固点降低：将溶质$B$溶入纯溶剂$A$中形成$B/A$稀溶液，若$A$与$B$不形成固态溶液，则溶液$B/A$的凝固点$T_f$低于纯溶剂的凝固点$T_f^{\ast }$称为稀溶液的凝固点降低。、
沸点升高：若向溶剂加入非挥发性溶质形成稀溶液，则溶液的沸点比纯溶剂的沸点高，称为稀溶液的沸点升高
渗透压：达到渗透平衡时，与溶剂液面同一高度的溶液截面上所受的压力与溶剂液面上所受压力之差称为溶剂的渗透压。

习题

在真空的容器中放入固态的$N{H}_{4}Cl$，在$520K$下分解为$N{H}_3(g)$与$HCl(g)$，平衡时容器内的压力为$66.66kPa$。
(1)计算$520K$时上述分解反应的标准平衡常数；
(2) 若容器中原来已经放置有$HCl(g)$气体，其压力为$39.99kPa$，求平衡时容器中气体的总压力；
(3) 若容器中原来已经放置有$NH3(g)$气体，其压力为$6.666kPa$，问需加多大压力的$HCl$，才能形成$N{H}_{4}Cl$。

$973K$时反应$FeO(s)+H_2(g)=Fe(s)+H_{2}O(g)$的$K_p^{\Theta}=0.426$
（1）$973K$下，用总压为$2p^{\Theta }$等摩尔$H_{2}O(g)$与$H_2(g)$的混合气体来处理$FeO(s)$。$FeO(s)$会被还原为$Fe(s)$吗？
（2）如果混合气体总压仍为$2p^{\Theta }$，要使$Fe(s)$不被氧化，$H_{2}O(g)$的分压最小应达多少

$第四章：化学平衡热力学$

1：$p100$ 化学反应等温方程式
2：$p111$ 各种因素对化学平衡的影响
3：计算，利用反应焓变和反应熵变的数据计算平衡常数，例4.5，范特霍夫公式求另一个温度的$k_P^{\Theta }$

1:以$p_B$表示组分$B$的分压，在无限大系统中反应的${\Delta }_r{G}_m^{\Theta }(T)$为：$${\Delta }_r{G}_m^{\Theta }(T)=\sum v_b{\mu }_B^{\Theta }(T)$$
为反应的标准摩尔吉布斯函数，其值由反应物的本性及温度决定，再令：$$J_p^{\Theta }=\prod _B(\frac{p_B}{p^{\Theta }}{)}^{v_B}$$其中定义$J_p^{\Theta }$为标准分压熵，与$K_p^{\Theta }(T)$的区别为这个为实际反应系统个反应组分的相对分压乘积的商，而后者为达到平衡时候的相对分压乘积的商。
以上，可得$${\Delta }_r{G}_m(T)={\Delta }_r{G}_m^{\Theta }(T)+RTln{J}_p^{\Theta }$$此式为化学反应等温方程式。
当化学反应达到平衡时，各组分的分压均为平衡分压，此时的标准分压商$J_p^{\Theta }$就是标准平衡分压商，即标准平衡常数$K_p^{\Theta }(T)$。又因平衡时${\Delta }_r{G}_m(T)=0$,故可将上式变为$${\Delta }_r{G}_m^{\Theta }(T)+RTln{K}_p^{\Theta }(T)=0$$将上述公式代入，可得$${\Delta }_r{G}_m(T)=-RTln{K}_p^{\Theta }(T)+RTln{J}_p^{\Theta }$$

2：各种因素对化学平衡的影响
各种因素对化学平很的影响可用勒夏特列原理定性的表述：一个化学反应如果已经达到化学平衡，当改变影响化学平衡的某一因素时，则平衡向着削弱这种改变的方向移动
1：温度对化学平衡的影响：由范特霍夫等压方程式可得:$$\frac{dln{K}_p^{\Theta }(T)}{dT}=\frac{{\Delta }_r{H}_m}{R{T}^2}$$
对于吸热反应，${\Delta }_r{H}_m>0$,则$\frac{dln{K}_p^{\Theta }(T)}{dT}>0$，$K_p^{\Theta }$随温度升高而增大，因此，升高温度使吸热反应的化学平衡正向移动，即像吸热反应的方向移动。对于放热反应，${\Delta }_r{H}_m<0$,则$\frac{dln{K}_p^{\Theta }(T)}{dT}<0$，$K_p^{\Theta }$随温度的升高而减小。因此，升高温度使放热反应的化学平衡逆向移动

2：浓度或分压对化学平衡的影响：根据化学的耐高温方程式进行分析：$${\Delta }_r{G}_m(T)={\Delta }_r{G}_m^{\Theta }(T)+RTln{J}_p^{\Theta }$$
当增大平衡系统中某反应物的分压，就会使$J_p^{\Theta }$分母增大，$J_p^{\Theta }$减小， 因此${\Delta }_r{G}_m(T)<0$，平衡将向反应正方向移动，当减小平衡系统中某反应物的分压，就会使$J_p^{\Theta }$分母变小，$J_p^{\Theta }$增大， 因此${\Delta }_r{G}_m(T)>0$，平衡将向反应逆方向移动，总之，增大平衡系统中某一组分的分压（或浓度），平衡将向减小该组分分压（或浓度）的方向移动。
3：总压对化学平衡的影响：根据：$$K_p^{\Theta }(T)=\prod _B(\frac{p_{B.e}}{p^{\Theta }}{)}^{v_B}$$以$p_{B,e}=y_B{p}_e$代入，可得$$K_p^{\Theta }(T)=(\frac{p_e}{p^{\Theta }}{)}^{\sum _B{v}_B}\prod _B{y}_B^{v_B}$$
定温下对指定的化学反应，若$\sum _B{v}_B=0$，则平衡总压$p_B$改变不会引起$(\frac{p_e}{p^{\Theta }}{)}^{\sum _B{v}_B}$的变化，故$\prod y_B^{v_B}$不变，对平衡无影响；若$\sum _B{v}_B>0$，$p_e$的增大会引起$(\frac{p_e}{p^{\Theta }}{)}^{\sum _B{v}_B}$的增大，为保持$K_p^{\Theta }(T)$不变，故$\prod y_B^{v_B}$下降，即平衡向逆反应方向移动，不利于产物生成；若$\sum _B{v}_B<0$，$p_e$的增大会引起$(\frac{p_e}{p^{\Theta }}{)}^{\sum _B{v}_B}$的减小，为保持$K_p^{\Theta }(T)$不变，故$\prod y_B^{v_B}$增大，即平衡向正反应方向移动，有利于产物生成。
总之：对于理想气体反应，增大总压，平衡向物质的量减少（体积收缩）的方向移动，减小总压，平衡将向物质的量增加（体积膨胀）的方向进行；若反应不会使物质的量或体积发生改变，则不会影响平衡组成

4：惰性气体及原料配比对化学平衡的影响：对于理想气体反应，加入惰性气体，平衡向使物质的量增加（体积膨胀）的方向进行，与减小系统总压产生的效果相同。

3：$例4.5反应MgC{O}_3(s)=MgO(s)+C{O}_2(g)有关热力学数据如下表$

$$\begin{gathered} (1)计算该反应的{\Delta }_r{G}_m^{\Theta }(298K)和K_p^{\Theta }(298K) \\ (2)计算298K下MgC{O}_3的分解压力。 \end{gathered}$$

$$\begin{gathered} (1):对于反应MgC{O}_3(s)=MgO(s)+C{O}_2(g) \\ {\Delta }_r{H}_m^{\Theta }(298K)=\sum _B{v}_B{\Delta }_f{H}_m(B,298K) \\ ={\Delta }_f{H}_m^{\Theta }[MgO(s),298K]+{\Delta }_f{H}_m^{\Theta }[C{O}_2(g),298K]+{\Delta }_f{H}_m^{\Theta }[MgC{O}_3(s),298K] \\ =[-601.2-393.5-(-1096.2)]kJ\cdot mo{l}^{-1}=101.5kJ\cdot mo{l}^{-1} \\ {\Delta }_r{S}_m^{\Theta }(298K)=\sum _B{v}_B{S}_m^{\Theta }(B,298K) \\ =S_m^{\Theta }[MgO(s),298K]+S_m^{\Theta }[C{O}_2(g),298K]-S_m^{\Theta }[MgC{O}_3(s),298K] \\ =(26.9+213.6-65.7)J\cdot K^{-1}\cdot mo{l}^{-1} \\ =184.8J\cdot K^{-1}\cdot mo{l}^{-1} \\ {\Delta }_r{G}_m^{\Theta }(298K)={\Delta }_r{H}_m^{\Theta }(298K)=T{\Delta }_r{S}_m^{\Theta }(298K) \\ =101.5kJ\cdot mo{l}^{-1}-287K\times 174.8J\cdot K^{-1}\cdot mo{l}^{-1}=49.4kJ\cdot mo{l}^{-1} \\ ln{K}_p^{\Theta }(298K)=-\frac{{\Delta }_r{G}_m(298K)}{R\times 298K}=-\frac{49.4kJ\cdot mo{l}^{-1}}{8.314J\cdot mo{l}^{-1}\cdot 298K}=-19.9 \\ (2):298K时MgC{O}_3的分解压力为： \\ {p}_e(C{O}_2)=p^{\Theta }{K}_p^{\Theta }(298K)=1\times 10^{5}Pa\times 2.28\times 10^{-9}=2.28\times 10^{-4}Pa \end{gathered}$$
另有公式，由已知化学反应的${\Delta }_r{H}_m$和温度$T_1$时的$K_p^{\Theta }(T1)$，可求得另一温度$T2$下的$K_p^{\Theta }(T2)$，公式如下$$ln\frac{K_p^{\Theta }(T2)}{K_p^{\Theta }(T1)}=\frac{{\Delta }_r{H}_m}{R}(\frac{1}{T1}-\frac{1}{T2})$$
·

$第五章：相平衡热力学$

1:$p122$,相率计算
2:p135：气液相图，恒沸混合物，恒沸体系
3：液固相图。p142水硫酸铵，p144稳定化合物相图，不稳定化合物相图，各个区自由度计算，特殊点计算。能够析出纯的固体，杠杠规则
4：冷却曲线画法，根据冷却曲线描述物体相态的变化

1：相律，也称吉布斯相律，研究相平衡系统中各种因素对系统相态的规律，可表述为：相平衡系统中，系统的自由度等于系统的独立组分数减去平衡的相数，再加上可影响平衡的外界条件数。即$$f=C-P+b$$
其中，$f$为自由度，$C$为独立组分数，$P$为相数，$b$为可影响相平衡的外界条件数。

独立组分数$C$的计算：足以形成相平衡系统中所有各项所需要的最少物种数称为独立组分数，若一个相平衡系统中有$S$种物质，且存在$R$个独立化学平衡以及$R^{{}^{\prime }}$个浓度限制条件，则$$C=S-R-R^{{}^{\prime }}$$$S$一般来说有几种物质就等于多少，$R$为化学平衡数，$R^{{}^{\prime }}$一般为隐形的限制条件，需要根据题目而定，物种数可能不同，但是最后的独立组分数是相同的。
$例：定温下PC{l}_5,PC{l}_3,C{l}_2三种气体组成的系统求C$
$$\begin{gathered} 解：由于有三种物质，所以S=3，存在化学平衡PC{l}_5(g)=PC{l}_3(g)+C{l}_2(g)，因此R=1，R^{{}^{\prime }}没有，所以C=3-1-0=2 \\ 如果规定[PC{l}_3]:[C{l}_2]=1:1，则R^{{}^{\prime }}=1,C=3-1-1=1 \end{gathered}$$

相数：平衡系统中所含相的数目称为相数，其中无论有多少种气体，相数总为$1$,有几项可以相互溶解的液体就有几项，通常有几种固体物质就有几相，固态溶液为一相
$例：水和苯有两项，C{O}_2和CO有一相$

自由度：独立变量数，看一定范围内，有多少变量可以随意改变，例如单组分相的水，有温度和压力可以随便改变，则$f=2$，若水和水蒸气两相，那么只有压力可以随意改变，则$f=1$
2：$$二组分完全互溶系统各种类型混合物的压力-组成图和温度-组成图$$

2:最低恒沸点，恒沸混合物：相图中最低点$C$处，气相线与液相线相交，与$C$点对应的系统气相组成和液相组成相同，即平衡蒸汽与液相组成相同，此时沸点恒定不变。又因为是液态混合物的最低沸点，故$C$点对应的温度称为最低恒沸点，与$C$点对应组成的混合物称为恒沸混合物。

最高恒沸点：最大负偏差混合物与最高点对应的温度称为最高恒沸点。

在一定压力下，恒沸混合物的沸点不变，从微观上来看，恒沸混合物的两组分其分子间并没有形成化学键；从宏观上来看，压力改变时，恒沸混合物的组成将改变，而化合物的化学组成却不会因为压力改变而改变
3：液-固相图，一共有$4$个重点相图
$1:H_{2}O-(N{H}_4{)}_{2}S{O}_4系统的温度-组成图$（p142）
相图分析：
$C$点：冰的熔点，该点$f=1-2+1=0$，由于高于$108.9^{\circ }$液相消失而成为水蒸气和盐的固体，盐的熔点无法标出
$O$点：三相点,$H_{2}O(s)\rightleftharpoons (N{H}_4{)}_{2}S{O}_4(s)\rightleftharpoons l$。$f=2-3+1=0$.组成在$O$点以左的溶液，冷却时先析出冰，以右的溶液冷却先析出$(N{H}_4{)}_{2}S{O}_4(s)$
$CO$线：冰，溶液两相共存时的组成曲线，也称为冰点下降曲线，线上$f=2-2+1=1$
$OD$线：$(N{H}_4{)}_{2}S{O}_4$固体与溶液两相共存时的溶液组成曲线，也称为盐的饱和溶度曲线，$f=2-2+1=1$
$EOF$线：冰，$(N{H}_4{)}_{2}S{O}_4$固体，溶液三相共存线，线上$f=2-3+1=0$
$COD$以上区：溶液单相区：$f=2-1+1=2$
$COE$区：冰与溶液两相共存区，$f=2-2+1=1$
$DOF$区：$(N{H}_4{)}_{2}S{O}_4$固体与溶液两相并存，$f=2-2+1=1$
$EOF$以下:$(N{H}_4{)}_{2}S{O}_4$固体与冰两相共存区，$f=2-2+1=1$

2:p144稳定化合物的二组分系统相图
$C_6{H}_{5}OH-C_6{H}_{5}N{H}_2系统相图$

$P$：$C_6{H}_{5}OH$的熔点
$Q$：$C_6{H}_{5}N{H}_2$的熔点
$R$：对应温度为$C$的熔点，相合熔点
$P,Q,R$点：$f=1-2+1=0$
$L$：$A$与$C$的低共熔点
$L^{{}^{\prime }}$：$C$与$B$的低共熔点
$L,L^{{}^{\prime }}$点：$f=2-3+1=0$
$PL、RL、R{L}^{{}^{\prime }}、Q{L}^{{}^{\prime }}$：两相平衡线，$f=2-2+1=1$
$L、L^{{}^{\prime }}$所在的水平线：三相水平线,$f=2-3+1=0$
单相区：$f=2-1+1=2$
两相区：$f=2-2+1=1$

3：形成不稳定化合物的热组分系统相图

$S$点对应温度为不稳定化合物$C$的分解温度，即不相合熔点
将$C$加热到$S$点对应温度，分解成$A$和$P$点对应组成的溶液，建立三项平衡：$$C(s)\rightleftharpoons l+A(s)$$PSQ线也为三相线:$$C(s)\rightleftharpoons l+A(s)$$与一般三相线不同的是：组成为$P$的溶液在端点，而不是在中间
4：由相图画出冷却曲线：自上而下你弯我也弯，你平我也平，注意横纵坐标，横坐标时间，纵坐标温度

5:杠杠规则，析出晶体：若以摩尔分数（或质量分数）表示系统及各项的组成，则呈平衡两相物质的量（或质量）反比与系统点到两个相点的线段长度，形式为$$\frac{m_L}{m_G}=\frac{{\omega }_G-{\omega }_a}{{\omega }_a-{\omega }_L}$$

习题

只受温度和压力影响的二组分平衡系统可能出现的最多相数为____。
$f=C-P+b=2-P+2，f_{min}=0,P_{max}=4$

硫酸与水能形成三种水合物：$H_{2}S{O}_4\cdot H_{2}O(s),H_{2}S{O}_4\cdot 2H_{2}O(s)$ 及$H_{2}S{O}_4\cdot 4H_{2}O(s)$。 在 $101.3kPa$下，与硫酸水溶液及冰共存的硫酸水合物最多为____种（压力对系统的影响可忽略)
相律$f=C-P+b$, 对于特定的系统，$C、b$都是固定值，因而相律反映出自由度数与相数的对应关系；并且$P\ge 1，f\ge 0$，当$f$ 取最小值时，相数$P$有最大值；当相数$P$取最小值时，自由度数$f$有最大值；注意对于固体，往往是系统中有几种固体，这几种固体就对应几相，固体的相数P就为几。本题中$C=2,b=1,f_{min}=0$, 则$P_{max}=3$，现在已有溶液和冰两相，则最多还可以形成一种水化物固体。

已知在下列系统中可发生反应$CaC{O}_3(s)=CaO(s)+C{O}_2(g)$ 和$BaC{O}_3(s)=BaO(s)+C{O}_2(g)$, 指出下列各系统的独立组分数和自由度：
(1) 由 $CaC{O}_3(s)、CaO(s)$和$C{O}_2(g)$组成的平衡系统。
(2) 将$CaC{O}_3(s)$ 放入抽空的密闭容器中形成的平衡系统。
(3) 由$CaC{O}_3(s)、CaO(s)、BaC{O}_3(s)、BaO(s)$ 和$C{O}_2(g)$构成的平衡系统。
(4) 将$CaC{O}_3(s)$和$BaC{O}_3(s)$放入抽空的密闭容器中形成的平衡系统。

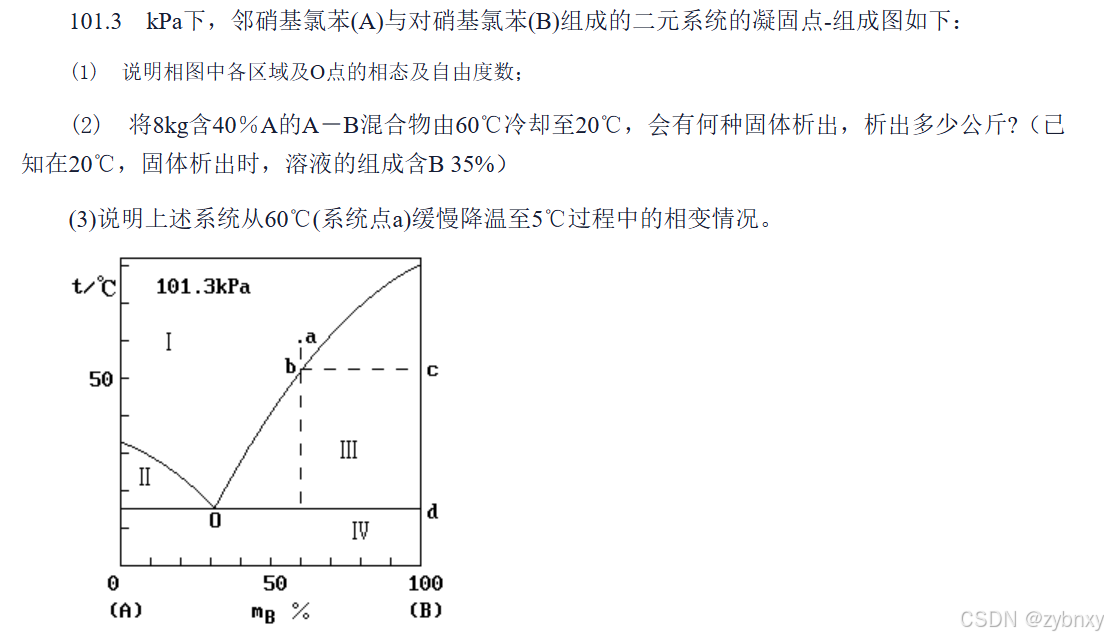
请按照$S、R、R^{\prime }、C、P、b、f$的顺序写出题目的各个参数。