算法设计——有 2n 的一个长方形方格，用一个12 的骨牌铺满方格。

最新推荐文章于 2024-06-04 13:40:32 发布

qq_43131391

最新推荐文章于 2024-06-04 13:40:32 发布

阅读量7.1k

点赞数 9

分类专栏：递归文章标签：笔记

本文链接：https://blog.csdn.net/qq_43131391/article/details/102417178

版权

递归专栏收录该内容

10 篇文章

订阅专栏

本文探讨了使用1x2骨牌铺满2xn长方形方格的算法，通过递推公式解决了任意n值时的铺法总数问题。文章首先给出了n=1和n=2时的基础情况，随后通过分析得出当n大于2时，铺法总数等于前两项之和，最终通过C++代码实现了该算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

有 2n 的一个长方形方格，用一个12 的骨牌铺满方格。

在这里插入图片描述
编写一个程序，试对给出的任意一个n(n>0), 输出铺法总数。
【算法分析】
　（1）当n=1时，
只能是一种铺法，铺法总数有示为x1=1。
　（2）当n=2时：
骨牌可以两个并列竖排，也可以并列横排，再无其他方法，如下左图所示，因此，铺法总数表示为x2=2；
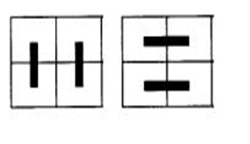
在这里插入图片描述
（3）当n=3时：

当n=3时的排列骨牌的方法数是n=1和n=2排列方法数的和。
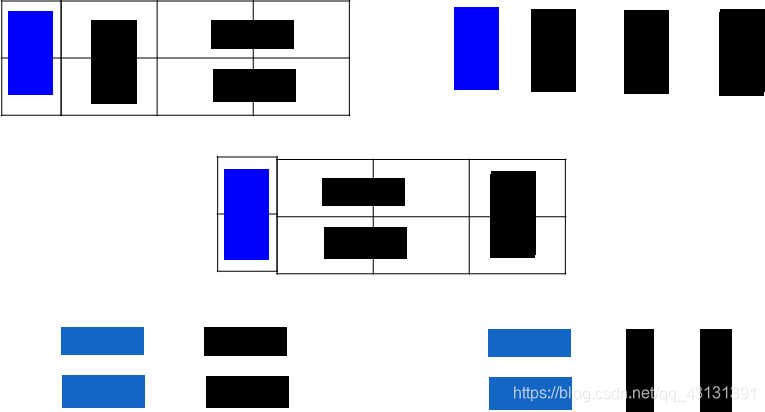
在这里插入图片描述

（4）当n=4时：
在这里插入图片描述

#include<iostream>
using namespace std;
int main(){
  int n,i,j,f[101];
  cout<<"input n:";                     //输入骨牌数
  cin>>n;
  f[1]=1;f[2]=2;  //边界条件
  cout<<“f[1]="<<f[1]<<endl;
  cout<<“f[2]="<<f[2]<<endl;
  for (i=3;i<=n;i++){               //递推过程
      f[i]=f[i-1]+f[i-2];
      cout<<“f["<<i<<"]="<<f[i]<<endl;
   }
}