为Cortex-M4编写优化的DSP代码

为Cortex-M4编写优化的DSP代码

本节展示如何使用优化指南和DSP指令来开发优化代码。我们看看Biquad（双二阶）滤波器，FFT蝴蝶操作和FIR滤波器。对于每个例子，我们都从通用的C代码开始，然后在应用优化策略时将其映射到Cortex-M4 DSP指令。

Biquad（双二阶）滤波器

Biquad双二阶滤波器是一种二阶递归或IIR滤波器。

双二阶滤波器是双二阶（两个极点和两个零点）的IIR滤波器。

双二阶滤波器在整个音频处理中用于均衡、音调控制、响度补偿、图形均衡器、交叉器等。高阶滤波器可以用Biquad的二阶部分来构造。

在许多应用程序中，Biquad滤波器是处理链中计算最密集的部分。它们也类似于在控制系统中使用的PID控制器，并且在本节中开发的许多技术直接应用于PID控制器。

二元滤波器是一个线性时不变系统。当滤波器的输入是正弦波时，输出是频率相同但幅度和相位不同的正弦波。输入和输出之间的幅度、相位关系称为滤波器的频率响应。二元滤波器有五个系数，频率响应由这些系数决定。通过改变系数，可以实现低通(lowpass)、高通(highpass)、带通(bandpass)、架子(shelf，分高架和低架)和陷波滤波器(notch，档位过滤器)。

例如，图21.3显示了音频“峰值滤波器”的幅度响应随着系数的变化而变化。滤波器系数通常由设计方程或使用工具如MATLAB生成。罗伯特·布里斯托-约翰逊已经为广泛的滤波器类型提供了计算Biquad系数的SUseful设计公式。

图21.3典型的二元滤波器的幅值响应。这种类型的滤波器被称为“峰值（peaking）滤波器”，提高或削减频率约1khz。图中显示了几个中心增益为0.1的变量。0.5。1.0。1.5。和2.0

直接形式I实现的Biquad滤波器结构如图21.4所示。输入$x[n]$到达并输入两条样本延迟线。标记为$z^{-1}$的盒子表示一个样本延迟。图的左侧为前馈处理，右侧为反馈处理。因为Biquad滤波器包含反馈，所以它也被称为递归滤波器。一个直接形式I的Biquad滤波器有5个系数，4个状态变量，每个输出样本总共取5个MACs。

直接形式I Biauad滤波器。这实现了一个二阶过滤器，是一个用于更高阶过滤器的构造块

由于图21.4所示的系统是线性的、不受时间影响的，所以我们可以切换前馈和反馈部分，如图21.5所示。通过这种改变，反馈和前馈部分的延迟线都采用相同的输入，因此可以合并。这将导致如图21.6所示的结构。这被称为直接形式II。直接形式II滤波器有五个系数，两个状态变量，每个输出样本总共需要5个MAC。直接形式I和直接形式ll滤波器在数学上是等价的。

在该图中，滤波器的前馈和反馈部分已经交换，两个延迟链接收相同的输入，可以组合如下图所示

与直接形式I相比，直接形式II过滤器的明显优势在于，它需要的状态变量数量只有前者的一半。每种结构的其他好处更加微妙。

如果你研究直接形式I滤波器，你会注意到输入状态变量保留了输入的延迟版本。类似地，输出状态变量包含输出的延迟版本。因此，如果过滤器的增益不超过1.0，那么状态变量在直接形式I将永远不会溢出。

另一方面，直接形式II滤波器中的状态变量与滤波器的输入或输出 没有直接关系。在实践中，直接形式II状态变量比滤波器的输入和输出具有更高的动态范围。因此，即使滤波器的增益不超过1.0，直接形式II中的状态变量也有可能超过1.0。

由于上述属性，直接形式I实现更适合于定点实现(更好的数值行为)，而直接形式II更适合于浮点实现(更少的状态变量)。

用于计算使用直接形式II实现的Biquad滤波器单级的标准C代码如下所示。该函数通过过滤器处理总共的blockSize大小样本。过滤器的输入来自缓冲区inPtr[]，输出写到outPtr[]。使用浮点运算:

// b0, b1, b2, a1, and a2 are the filter coefficients.
// a1 and a2 are negated.
// stateA, stateB, and stateC represent intermediate state
variables.
for (sample = 0; sample < blockSize; sample++)
{
stateA = *inPtr++ + a1*stateB + a2*stateC;
*outPtr++ = b0*stateA + b1*stateB + b2*stateC;
stateC = stateB;//先保存stateB信息
stateB = stateA;//更新新的stateB信息
}
// Persist state variables for the next call
state[0] = stateB;
state[1] = stateC;

带领中间状态变量stateA、stateB和stateC如图21.6所示。接下来，我们将检查函数的内循环，看看需要多少循环。我们将把操作分解为独立的Cortex-M4指令:

stateA = *inPtr++; // Data fetch [2 cycles]
stateA += a1*stateB; // MAC with result used in next inst [4 cycles]
stateA += a2*stateC; // MAC with result used in next inst [4 cycles]

out = b0*stateA; // Mult with result used in next inst [2 cycles]
out += b1*stateB; // MAC with result used in next inst [4 cycles]
out += b2*stateC; // MAC with result used in next inst [4 cycles]
*outPtr++ = out; // Data store [2 cycles]

stateC = stateB; // Register move [1 cycle]
stateB = stateA; // Register move [1 cycle]
// Loop overhead [3 cycles]

全部合在一起，通用C代码的内部循环总共需要每个示例执行27个周期。 优化函数的第一步是将MAC指令拆分为单独的乘法和加法。 然后重新排序计算，以便在下一个周期中不需要浮点操作的结果。 一些附加变量用于保存中间结果：

stateA = *inPtr++ // Data fetch [2 cycles]
prod1 = a1*stateB; // Mult [1 cycle]
prod2 = a2*stateC; // Mult [1 cycle]

stateA += prod1; // Addition [1 cycle]
stateA += prod2; // Add [1 cycle]

prod3 = b0*stateA // Mult [1 cycle]
prod4 = b1*stateB; // Mult [1 cycle]

out = b2*stateC; // Mult [1 cycle]
out += prod4; // Add [1 cycle]
out += prod3; // Add [1 cycle]

stateC = stateB; // Register move [1 cycle]
stateB = stateA; // Register move [1 cycle]
*outPtr++ = out; // Data store [2 cycles]
// Loop overhead [3 cycles]

直接形式II Biquad结构。这需要5次乘法，但只有两次延迟。在做浮点处理时，它是首选的

这些变化将Biquad的内环从27周期减少到18周期。 这是朝着正确的方向迈出的一步，但有三种技术可以应用于Biquad，以便进一步改进：

1. 通过仔细使用中间变量来消除寄存器的移动。 结构中从上到下的状态变量最初是：
   stateA, stateB, stateC
   在计算第一个输出之后，状态变量向右移动。 我们不会真正地转移变量，而是使用排序来重用它们：
   stateC, stateA, stateB
   下一次迭代后，状态变量重新排序为：
   stateB, stateC, stateA
   最后，在第四次迭代之后，变量是：
   stateA, stateB, stateC
   循环然后重复，它有一个自然周期3个样本。 也就是说，如果我们从开始：
   stateA, stateB, stateC
   然后，在计算了3个输出样本之后，我们将返回到：
   stateA, stateB, stateC
2. 将循环展开3倍，以减少循环开销。 循环开销3个周期将摊销超过3个样本。
3. 组加载和存储指令。 在上面的代码中，负载和存储指令是隔离的，每个指令需要2个周期。 通过加载和存储几个结果，第二次和随后的内存访问只需要1个周期。 由于循环展开，结果代码现在要长一些：

//3个一组进行加载
in1 = *inPtr++; // Data fetch [2 cycles]
in2 = *inPtr++; // Data fetch [1 cycles]
in3 = *inPtr++; // Data fetch [1 cycles]

prod1 = a1*stateB; // Mult [1 cycle]
prod2 = a2*stateC; // Mult [1 cycle]
stateA = in1+prod1; // Addition [1 cycle]
prod4 = b1*stateB; // Mult [1 cycle]
stateA += prod2; // Add [1 cycle]
out1 = b2*stateC; // Mult [1 cycle]
prod3 = b0*stateA; // Mult [1 cycle]
out1 += prod4; // Add [1 cycle]
out1 += prod3; // Add [1 cycle]

prod1 = a1*stateA; // Mult [1 cycle]
prod2 = a2*stateB; // Mult [1 cycle]
stateC = in2+prod1; // Addition [1 cycle]
prod4 = b1*stateA; // Mult [1 cycle]
stateC += prod2; // Add [1 cycle]
out2 = b2*stateB; // Mult [1 cycle]
prod3 = b0*stateC; // Mult [1 cycle]
out2 += prod4; // Add [1 cycle]
out2 += prod3; // Add [1 cycle]

prod1 = a1*stateC; // Mult [1 cycle]
prod2 = a2*stateA; // Mult [1 cycle]
stateB = in3+prod1; // Addition [1 cycle]
prod4 = b1*stateC; // Mult [1 cycle]
stateB += prod2; // Add [1 cycle]
out3 = b2*stateA; // Mult [1 cycle]
prod3 = b0*stateB; // Mult [1 cycle]
out3 += prod4; // Add [1 cycle]
out3 += prod3; // Add [1 cycle]

outPtr++ = out1; // Data store [2 cycles]
outPtr++ = out2; // Data store [1 cycles]
outPtr++ = out3; // Data store [1 cycles]
// Loop overhead [3 cycles]

计数周期我们最终有38个周期来计算3个输出样本或每个样本12.67个周期。 这里介绍的代码对长度为3个样本的倍数的向量进行操作。 为了通用性，代码需要另一个阶段，它处理剩余的1或2个样本；这不显示。

有可能进一步优化吗?我们可以把环展开多远?该滤波器的核心算术运算包括5次乘法和4次加法。这些操作，当正确命令避免摊位在Cortex-M4上需要9个周期。内存加载和存储每个最多需要1个周期。把这些放在一起，一个Biquad的绝对最小循环数是每个样本11个循环。这假设所有的数据加载和存储都是1个周期，并且没有循环开销。如果我们进一步展开内部循环，我们会发现:

在某些情况下，处理器用完了保存输入和输出变量的中间寄存器，就不可能再得到进一步的好处了。展开3或6个样本是合理的选择。除此之外，收益微乎其微。

快速傅里叶变换

快速傅里叶传输(FFT)是一种用于频域处理、压缩和快速滤波算法的关键信号处理算法。FFT实际上是一种计算离散傅里叶变换(DFT)的快速算法。DFT变换将N点时域信号x[nl]分解为N个单独的频率分量x[kl]，其中每个分量都是一个复值，包含幅度和相位信息。

长度为N的有限长度序列的DFT定义为:
$X[K]={\sum }_{n=0}^{N-1}x[n]W_N^{kn}$ ，$k=0,1,2,...,N-1$

其中$W_N^k$是一个复值，表示$k$次单位根：
$W_N^K=e^{-j2\pi k/N}=cos(2\pi k)-j\ast sin(2\pi k)$

n次单位根是n次幂为1的复数，他们位于复平面的单位元上，构成正n边形的顶点。其乘法构成n阶乘法群

从频域到时域的逆变换几乎是相同的:
$x[n]=\frac{1}{N}{\sum }_{n=0}^{N-1}X[k]W_N^{-kn}$ ，$n=0,1,2,...,N-1$

直接实现上述公式需要O(N2)操作来计算所有N个正变换或反变换样本。使用FFT，我们将看到这简化为O(NlogN)操作。对于较大的N值，节省的费用是可观的，而且FFT已经使许多新的信号处理应用成为可能。FFT最初由Cooley和Tukey在1965年描述(文章)，这里可以找到一个很好的FFT算法的一般参考。

当长度N是一个合数（能够被1以外的整数整除），可以表示为小因子的乘积时，FFTs通常工作得最好:
$N=N_1\times N_2\times N_3...N$
最简单的算法是那些N是2的幂的情况，它们被称为radix-2变换（2点变换）。

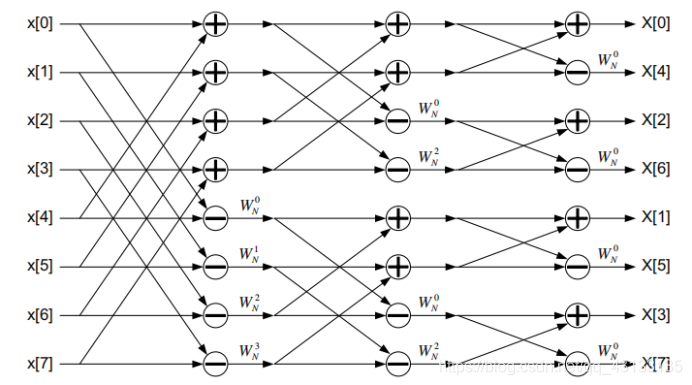
FFT采用“分而治之”算法，N点FFT的计算使用两个单独的N/2点变换和一些额外的操作。fft主要有两类:时域抽取和频域抽取。实时抽取算法通过结合偶数和奇数时域样本的N/2点FFT计算N点FFT。频率抽取算法是相似的，计算偶数和奇数频域样本使用两个N/2点FFTs。这两种算法都有相似数量的数学运算。CMSIS库使用频率抽取算法，我们将着重讨论这些算法。8点radix-2抽取频率FFT的第一阶段如图21.7所示。

8点变换是使用两个单独的4点变换计算的。前面定义的乘法因子W出现在上面，其值称为旋转因子。为了提高速度，旋转因子是预先计算并存储在数组中，而不是在FFT函数本身中计算。继续分解，4点fft被分解为两个2点fft。最后，计算四个两点fft。最终的结构如图21.8所示。注意，一个8点FFT的总体结构, 有3个阶段，每个阶段由4只蝴蝶组成。

每个阶段由4个蝴蝶操作组成，图21.9显示了单个蝴蝶每个蝴蝶都包含复杂的加法、减法和乘法。

蝴蝶操作的一个特性是它可以在内存中就地完成。也就是说，获取复值a和b，执行操作，然后将结果放回数组相同位置的内存中。事实上，整个FFT可以在输入输入的相同缓冲区中生成输出。

输入如图21.8是在正常秩序和收益按顺序从x[0]到x[7]。对处理后的输出进行置乱，其顺序称为逆位顺序:为了理解顺序，将索引0 - 7写入二进制，将位翻转180度，再转换回十进制:

位反向排序是就地处理的一个自然副作用。大多数FFT算法(包括在CMSIS DSP库中的算法)提供了将输出值重新排序回到顺序顺序的选项。

蝴蝶操作是FFT算法的核心，我们将在本节中分析和优化单个蝴蝶的计算。 八点FFT需要3*4=12只蝴蝶。 一般来说，长度为N的radix-2(基数为2)FFT有$lo{g}_{2}N$阶段，每个阶段有N=2只蝴蝶，总共有$（N/2）lo{g}_{2}N$只蝴蝶。

分解成蝴蝶产生FFT的$O（Nlo{g}_{2}N）$操作计数。 除了蝴蝶本身，FFT还需要索引，以跟踪算法的每个阶段应该使用哪些值。 在我们的分析中，我们将忽略这个索引开销，但它必须在最终的算法中考虑。

浮点蝴蝶的C代码如下所示，变量index1和index2是蝴蝶的两个输入的数组偏移量。 数组x[]保存交错数据(real、imag、real、imag等)。

// Fetch two complex samples from memory [5 cycles] 
x1r = x[index1]; 
x1i = x[index1+1]; 
x2r = x[index2]; 
x2i = x[index2+1]; 
// Compute the sum and difference [4 cycles] 
sum_r = (x1r + x2r); 
sum_i = (x1i + x2i); 
diff_r = (x1r - x2r); 
diff_i = (x1i - x2i); 
// Store sum result to memory [3 cycles] 
x[index1] = sum_r; 
x[index1+1] = sum_i; 
// Fetch complex twiddle factor coefficients [2 cycles] 
twiddle_r = *twiddle++; 
twiddle_i = *twiddle++; 
// Complex multiplication of the difference [6 cycles] 
prod_r = diff_r * twiddle_r - diff_i * twiddle_i; 
prod_i = diff_r * twiddle_i + diff_i * twiddle_r; 
// Store back to memory [3 cycles] 
x[index2] = prod_r; 
x[index2+1] = prod_i;

代码还显示了各种操作的周期计数，我们看到一只蝴蝶在Cortex-M4上需要23个周期。 更仔细地观察周期计数，我们看到13个周期是由于内存访问，10个周期是由于算术。通过将内存访问分组在一起，花费在内存访问上的总周期数可以减少到11。

即便如此。在Cortex-M4上，radix-2 butterfly的主要功能是内存访问，这对于整个FFT算法来说是正确的。在加速图21.10所示的radix-2 FFT蝴蝶上几乎没有什么可做的。相反，为了提高性能，我们需要考虑更高的基数算法。在radix-2算法中。我们一次处理两个复数值总共有log2N个处理阶段。在每个阶段，我们需要加载N个复值对它们进行操作，然后将它们存储回内存中。在radix-4算法中，我们一次对4个复值进行操作，总共有log N个阶段。这样内存访问就减少了1 / 2。只要中间寄存器没有用完，可以考虑较高的radix。

我们发现在Cortex-M4和radix-8蝴蝶上，最多可以使用浮点数在定点上有效地实现radix-4蝴蝶。radix-4算法被限制为FFT长度，为4的幂:{4, 16, 64,256, 1024, etc.}。而radix-8算法被限制为长度为{8,64,512,4096 etc.}。为了有效地实现任意长度(2的幂)，采用了阿米切-基数算法。诀窍是使用尽可能多的radix-8阶段(它们是最高效的)，然后根据需要使用单个radix-2或radix-4阶段来达到所需的长度。 下面是各种FFT长度如何分解成蝴蝶阶段：

在CMSIS DSP库中，FFT函数使用这种混合基数方法来处理浮点数据类型。 对于定点，必须选择radix-2或radix-4。 一般情况下，选择radix-4定点算法，如果它支持你想要的长度。

许多应用还要求计算FFT逆变换。

通过对正、逆DFT方程的比较，我们发现逆变换具有(1/N)的标度因子，并且旋转因子指数的符号是倒置的。 这导致了两种不同的实现逆FFT的方法：

1. 计算前向FFT，但使用一个新的旋转因子表。 新表是使用正指数而不是负指数创建的。 这导致旋转因子简单地被共轭。 除以N。
2. 保持与以前相同的旋转因子表，但修改FFT代码，以否定旋转因子表的虚部，同时执行旋转因子乘法。 再除以N。

上述两种方法都有一些低效率。

方法(1) 节省代码空间，但将旋转因子表的大小增加一倍；
方法(2) 重用旋转因子表，但需要更多的代码。

另一种方法是使用数学关系:
$IFFT(X)=\frac{1}{N}conj(FFT(conj(X))$

这需要将数据结合两次。 第一（内)共轭是在开始时完成的，第二共轭(外）可以与N的除法相结合。与方法（2）相比，这种方法的实际开销大致只有内共轭，这是可以接受的。

在定点实现FFT时，了解整个算法中值的缩放和增长是至关重要的。 蝴蝶执行一个和差，它是可能的值在蝴蝶的输出是双倍的输入。

在最坏的情况下，每个阶段的值都是两倍，输出比输入大N倍。 直观地说，如果所有输入值等于1.0，则发生最坏的情况。这表示一个直流（DC）信号，除了bin k= 0包含一个N的值外，得到的FFT全是零。为了避免定点实现中溢出，每个butterfly阶段必须包含一个0.5的比例作为加减法的一部分。这实际上是CMSIS DSP库中定点FFT函数所使用的缩放，最终结果是FFT的输出被缩放1/N。

标准的FFT操作在复杂的数据上，有一些变化用于处理真实数据。通常，n点实FFT是使用复数计算的N/2点FFT加上一些额外的步骤。

FIR滤波器

我们将考虑的第三个标准DSP算法是FIR(有限脉冲响应)滤波器。

FIR滤波器出现在各种音频、视频、控制和数据分析问题中。 与IIR滤波器(如Biquad)相比，FIR滤波器具有几个有用的特性:

1. 过滤器本质上是稳定的。这对所有可能的系数都成立
2. 线性相位可以通过使系数对称来实现。
3. 简单的设计公式。
4. 即使在使用定点实现时也表现良好。

设x[n]时间n时滤波器的输入，y[n]为输出。利用差分方程计算输出:
$y[n]={\sum }_{k=0}^{N-1}x[n-k]h[k]$
其中h[k]是滤波器系数。 在上述差分方程中，FIR滤波器具有N个系数： { h [ 0 ] , h [ 1 ] , . . . , h [ N − 1 ] } \{h[0], h[1],...,h[N-1]\} {h[0],h[1],...,h[N−1]}

前面的输入样本称为状态变量。滤波器的每个输出都需要N次乘法和N-1次加法。现代DSP可以在大约N个周期内计算一个N点FIR滤波器。

在内存中组织状态数据的最直接的方法是使用FIFO。

如图21.11所示。当样本x[n]到达时，将之前的样本x[n-1]到x[n-N]向下移动一个位置，然后将x[n]写入到缓冲区中。像这样移动数据是非常浪费的，每个输入样本需要N-1个内存读和N-1个内存写。

使用移位寄存器实现FIR过滤器。 在实践中，这很少被使用，因为每当一个新的样本到达时，状态变量必须正确地移动