支持向量机
我们对支持向量机的理解,可以用二维来说明,比如需要找一条最优的直线(超平面)将两类点分开:
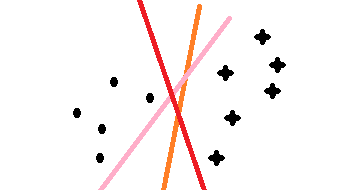
不过这里需要定义一下说明是最优,那就是:
使得离直线较近的点具有最大间距
如下有5个蓝色样本,标记为y =1,紫色有5个样本,标记为 y=-1,共10个样本:
{
(
x
₁
,
y
₁
)
,
(
x
₂
,
y
₂
)
.
.
.
.
.
.
.
.
.
(
x
10
,
y
10
)
}
\{(x₁ ,y₁) , (x₂,y₂) .........(x_{10},y_{10}) \}
{(x₁,y₁),(x₂,y₂).........(x10,y10)} 。
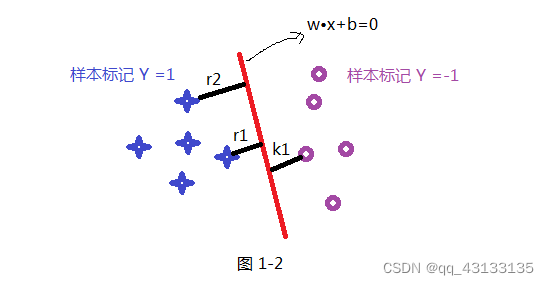
平面(分割线)为
w
T
⋅
x
+
b
⋅
1
=
0
w^T\cdot x+b\cdot 1=0
wT⋅x+b⋅1=0
我们都知道,该方程相当于齐次向量 [ x , 1 ] [x,1] [x,1]在某个向量 [ w , b ] [w,b] [w,b]上的投影,这点和感知机异曲同工。
其中 [ w , b ] [w,b] [w,b]这个向量恰好与图中所示的直线对应齐次向量 [ x , 1 ] [x,1] [x,1]垂直,故内积为0
样本点到超平面的距离即为 x i x_i xi在向量 w w w的投影再加上b,即 w T ⋅ x + b ⋅ 1 w^T\cdot x+b\cdot 1 wT⋅x+b⋅1,不过我们知道这个投影值可能是负的,我们再加一个符号纠正项即可: y i × y ( x i ) y_i\times y(x_i) yi×y(xi)
式中 y i y_i yi的作用,便是纠正 y ( x i ) y(x_i) y(xi)的符号,使得当 x i x_i xi投影结果 y ( x i ) y(x_i) y(xi)为负数时,由于 y i = − 1 y_i=-1 yi=−1,使得负负得正。
点到平面距离定义
所以我们可以定义出任意样本点的距离,为超平面(w, b)关于训练数据集的函数间隔 y i ⋅ y ( x i ) y_i\cdot y(x_i) yi⋅y(xi)
但是这样简单定义的距离存在的问题是:
对于向量 2 ⋅ [ w , b ] 2\cdot[w,b] 2⋅[w,b],显然也满足方程,这样算出来的投影必然是之前的两倍,这会使得距离函数不具有唯一性。
考虑到 x = x 0 + w T ⋅ r x=x_0 + w^T \cdot r x=x0+wT⋅r,其中 x 0 x_0 x0为分割直线上的点,恰好使得法向量 w w w方向的投影值为-b:
w T ⋅ x + b = 0 w^T\cdot x+b=0 wT⋅x+b=0,即 w T ⋅ x = − b w^T\cdot x= -b wT⋅x=−b
我们只需要将法向量归一化即可,即有:
x
=
x
0
+
w
∣
∣
w
∣
∣
⋅
r
x=x_0 + \frac{w}{||w||} \cdot r
x=x0+∣∣w∣∣w⋅r
其中
r
r
r即为投影距离。
将 x = x 0 + w T ∣ ∣ w ∣ ∣ ⋅ r x=x_0 + \frac{w^T}{||w||} \cdot r x=x0+∣∣w∣∣wT⋅r 带入原来方程 y ( x ) = w T ⋅ x + b ⋅ 1 y(x)=w^T\cdot x+b\cdot 1 y(x)=wT⋅x+b⋅1
可得: y ( x ) = w T ⋅ x 0 + w T ⋅ w ∣ ∣ w ∣ ∣ ⋅ r + b ⋅ 1 y(x)=w^T\cdot x_0 +w^T\cdot \frac{w}{||w||} \cdot r+b\cdot 1 y(x)=wT⋅x0+wT⋅∣∣w∣∣w⋅r+b⋅1
由于 w T ⋅ x 0 = − b w^T\cdot x_0 =-b wT⋅x0=−b, w T ⋅ w = ∣ ∣ w ∣ ∣ 2 w^T\cdot w =||w||^2 wT⋅w=∣∣w∣∣2,化简为:
y ( x ) = ∣ ∣ w ∣ ∣ ⋅ r y(x)=||w|| \cdot r y(x)=∣∣w∣∣⋅r
所以我们可以算出距离函数
r
i
r_i
ri:
r
i
=
y
(
x
i
)
∣
∣
w
∣
∣
r_i=\frac{y(x_i)}{||w||}
ri=∣∣w∣∣y(xi)
加上之前的符号修正,即有:
r
i
=
y
i
⋅
y
(
x
i
)
∣
∣
w
∣
∣
r_i=\frac{y_i\cdot y(x_i)}{||w||}
ri=∣∣w∣∣yi⋅y(xi)
凸优化训练
我们的目的就是找到使得最近的点
i
i
i到直线具有最大间距:
γ
=
m
a
x
[
w
,
b
]
{
r
i
}
\gamma =max_{[w,b]}\{r_i\}
γ=max[w,b]{ri}
注意:最近的点会随着法向量方向改变而发生变化,并不是一个固定点
所以对于任意点
i
i
i,我们会有
r
i
≥
γ
r_i ≥ \gamma
ri≥γ,即
y
i
⋅
y
(
x
i
)
∣
∣
w
∣
∣
≥
γ
\frac{y_i\cdot y(x_i)}{||w||}≥ \gamma
∣∣w∣∣yi⋅y(xi)≥γ
两边同除
γ
\gamma
γ得:
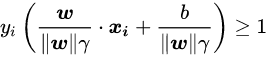
由于我们之前就注意到,对于[w,b],他们同时扩大相同的倍数,并不会改变分类结果,所以对于缩小
∣
∣
w
∣
∣
||w||
∣∣w∣∣还是
∣
∣
w
∣
∣
⋅
γ
||w||\cdot \gamma
∣∣w∣∣⋅γ倍,其实也不会改变分类结果
只是分类结果不改变,但是若作为距离肯定就发生改变了,所以令新的 w = w ∣ ∣ w ∣ ∣ ⋅ γ w=\frac{w}{||w||\cdot \gamma} w=∣∣w∣∣⋅γw, b = b ∣ ∣ w ∣ ∣ ⋅ γ b=\frac{b}{||w||\cdot \gamma} b=∣∣w∣∣⋅γb
即有:
对于这个新的 w w w而言, γ \gamma γ越大,它的长度就越小
对于 w ∣ ∣ w ∣ ∣ \frac{w}{||w||} ∣∣w∣∣w而言,其模长为1,所以新的 w w w相当于单位向量除以 γ \gamma γ
所以我们取得最大的
γ
\gamma
γ,等价于新的
w
w
w模长将最小,即有
m
i
n
{
w
2
}
min\{w^2\}
min{w2},为了便于后面二次函数求导结果好看,我们加了一项,得到:
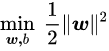
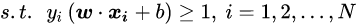
这是一个含有不等式约束的凸二次规划问题,可以对其使用拉格朗日乘子法得到其对偶问题:
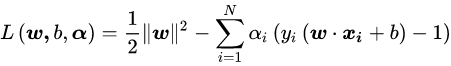
后续即可推导结果
更多参考文章:
Svm算法原理及实现
支持向量机(SVM)——原理篇







 本文详细介绍了支持向量机(SVM)的概念,通过二维空间的示例解释了如何寻找最优超平面以最大化间隔。讨论了样本点到超平面的距离计算,以及如何通过凸优化确保最近的样本点到超平面的最大距离。最终,提出了通过拉格朗日乘子法解决约束的凸二次规划问题,以求得最优解。
本文详细介绍了支持向量机(SVM)的概念,通过二维空间的示例解释了如何寻找最优超平面以最大化间隔。讨论了样本点到超平面的距离计算,以及如何通过凸优化确保最近的样本点到超平面的最大距离。最终,提出了通过拉格朗日乘子法解决约束的凸二次规划问题,以求得最优解。

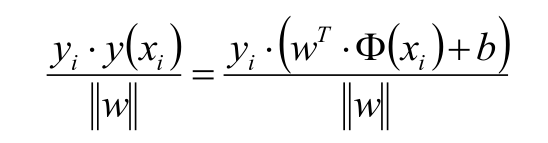

















 1624
1624

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








