【工具代码】解多元一次方程

背景

写一些作业的时候总是要解多元一次方程（特别是电路分析），手算很麻烦又容易出错，索性写了一个C++代码用来方便的求解多元一次方程的解。

使用方式

先输入未知数个数n
然后输入n个方程。
输入示例：
比如有3个未知数$x_0,x_1,x_2$
三个方程为：
$x_0+x_1+x_2=1$
$x_0-2x_2=9$
$x_1+4x_2=10$

那么输入就应该是：

3
1 1 1 1
1 0 -2 9
0 1 4 10

输出为：

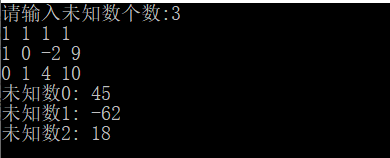
用高斯消元写的，所以复杂度是$O(N^3)$

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
double a[20][20];
const double eps = 1e-9;
void change(int x, int y, int n){//交换行
    for(int j = 0; j <= n; ++j) swap(a[x][j], a[y][j]);
}
int n;
double ans[20];
void guess()
{
    for(int i = 0; i < n; ++i){
        if(a[i][i] < eps && a[i][i] > -eps){//如果这一位为0
            for(int j = i+1; j < n; ++j) {//找到这一位不为0的交换
                if(abs(a[j][i]) > eps) change(i, j, n);
            }
        }
        if(a[i][i] < eps && a[i][i] > -eps){
            cout<<"输入矩阵存在线性相关向量，请检查！"<<endl;
            return;
        }
        for(int j = i+1; j < n; ++j){
            if(a[j][i] < eps && a[j][i] > -eps) continue;//该位为0，不用管
            double t = a[j][i]/a[i][i];
            for(int k = i; k <= n; ++k){
                a[j][k] -= a[i][k]*t;
            }
        }
    }//处理出上三角矩阵
    for(int i = n-1; i >= 0; --i){
        ans[i] = a[i][n];
        for(int j = n-1; j > i; --j){
            ans[i] -= ans[j]*a[i][j];
        }
        ans[i] /= a[i][i];
    }
}
double pl, pr;
int main()
{
	cout<<"请输入未知数个数:";cin>>n;
	for(int i = 0; i < n; ++i) for(int j = 0; j <= n; ++j) cin>>a[i][j];
	guess();
	for(int i = 0; i < n; ++i){
        cout<<"未知数"<<i<<": "<<ans[i]<<endl;
	}
}
/*
4
1.2 -1 0 -0.1 1
-1 2.0005 -0.0005 0 -0.5
0 -0.0005 0.7505 -0.25 0.5
-0.1 0 -0.25 0.6 0
*/