力扣第 418 场周赛

Java吃不到羊的狼

于 2024-10-09 16:20:43 发布

阅读量412

点赞数 10

分类专栏： Leetcode周赛复盘文章标签： leetcode 算法数据结构

本文链接：https://blog.csdn.net/qq_43227507/article/details/142788627

版权

Leetcode周赛复盘专栏收录该内容

8 篇文章 0 订阅

订阅专栏

3309. 连接二进制表示可形成的最大数值

给你一个长度为 3 的整数数组 nums。现以某种顺序连接数组 nums 中所有元素的 二进制表示 ，请你返回可以由这种方法形成的最大数值。注意任何数字的二进制表示不含前导零。

示例 1:

输入: nums = [1,2,3]

输出: 30

解释:

按照顺序 [3, 1, 2] 连接数字的二进制表示，得到结果 "11110"，这是 30 的二进制表示。

示例 2:

输入: nums = [2,8,16]

输出: 1296

解释:

按照顺序 [2, 8, 16] 连接数字的二进制表述，得到结果 "10100010000"，这是 1296 的二进制表示。

提示:

nums.length == 3
1 <= nums[i] <= 127

思路：如代码所示

class Solution {
    public int maxGoodNumber(int[] nums) {
         // 将整数转换为二进制字符串
        String[] binaryStrs = new String[nums.length];
        for (int i = 0; i < nums.length; i++) {
            binaryStrs[i] = Integer.toBinaryString(nums[i]);
        }

        // 按照连接后的结果进行排序
        Arrays.sort(binaryStrs, new Comparator<String>() {
            @Override
            public int compare(String a, String b) {
                return (b + a).compareTo(a + b); // 连接后比较
            }
        });

        // 连接排序后的二进制字符串
        StringBuilder sb = new StringBuilder();
        for (String str : binaryStrs) {
            sb.append(str);
        }

        // 将结果转换为十进制
        return Integer.parseInt(sb.toString(), 2);
    }
}

3310. 移除可疑的方法

你正在维护一个项目，该项目有 n 个方法，编号从 0 到 n - 1。

给你两个整数 n 和 k，以及一个二维整数数组 invocations，其中 invocations[i] = [ai, bi] 表示方法 ai 调用了方法 bi。

已知如果方法 k 存在一个已知的 bug。那么方法 k 以及它直接或间接调用的任何方法都被视为 可疑方法 ，我们需要从项目中移除这些方法。

只有当一组方法没有被这组之外的任何方法调用时，这组方法才能被移除。

返回一个数组，包含移除所有 可疑方法 后剩下的所有方法。你可以以任意顺序返回答案。如果无法移除所有可疑方法，则不移除任何方法。

示例 1:

输入: n = 4, k = 1, invocations = [[1,2],[0,1],[3,2]]

输出: [0,1,2,3]

解释:

方法 2 和方法 1 是可疑方法，但它们分别直接被方法 3 和方法 0 调用。由于方法 3 和方法 0 不是可疑方法，我们无法移除任何方法，故返回所有方法。

示例 2:

输入: n = 5, k = 0, invocations = [[1,2],[0,2],[0,1],[3,4]]

输出: [3,4]

解释:

方法 0、方法 1 和方法 2 是可疑方法，且没有被任何其他方法直接调用。我们可以移除它们。

示例 3:

输入: n = 3, k = 2, invocations = [[1,2],[0,1],[2,0]]

输出: []

解释:

所有方法都是可疑方法。我们可以移除它们。

提示:

1 <= n <= 10^5
0 <= k <= n - 1
0 <= invocations.length <= 2 * 10^5
invocations[i] == [ai, bi]
0 <= ai, bi <= n - 1
ai != bi
invocations[i] != invocations[j]

分析：一个项目有 n 个方法，其中第 k 个方法有 bug。可能是第 k 个方法自己的 bug，也可能是第 k 个方法调用的更底层的方法有 bug。

你需要删除所有可能有 bug 的方法。如果删除后无法编译（剩余的方法调用了删除的方法），那么返回数组 [0,1,2,⋯,n−1]。

如果可以正常删除，返回剩余的方法编号。

思路：从 k 开始 DFS 图，标记所有可能有 bug 的方法（节点）。题目把这些方法叫做可疑方法。
遍历 invocations，如果存在从「非可疑方法」到「可疑方法」的边，则删除后无法编译，返回数组 [0,1,2,⋯,n−1]。
否则可以正常删除，把非可疑方法加入答案。
图中可能有环，为避免 DFS 无限递归下去，只需 DFS 没有访问过（没有被标记）的节点。

代码：

class Solution {
    public List<Integer> remainingMethods(int n, int k, int[][] invocations) {
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int[] e : invocations) {
            g[e[0]].add(e[1]);
        }

        // 标记所有可疑方法
        boolean[] isSuspicious = new boolean[n];
        dfs(k, g, isSuspicious);

        // 检查是否有【非可疑方法】->【可疑方法】的边
        for (int[] e : invocations) {
            if (!isSuspicious[e[0]] && isSuspicious[e[1]]) {
                // 无法移除可疑方法
                List<Integer> ans = new ArrayList<>(n);
                for (int i = 0; i < n; i++) {
                    ans.add(i);
                }
                return ans;
            }
        }

        // 移除所有可疑方法
        List<Integer> ans = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (!isSuspicious[i]) {
                ans.add(i);
            }
        }
        return ans;
    }

    private void dfs(int x, List<Integer>[] g, boolean[] isSuspicious) {
        isSuspicious[x] = true;
        for (int y : g[x]) {
            if (!isSuspicious[y]) { // 避免无限递归
                dfs(y, g, isSuspicious);
            }
        }
    }
}

3311. 构造符合图结构的二维矩阵

给你一个二维整数数组 edges ，它表示一棵 n 个节点的无向图，其中 edges[i] = [ui, vi] 表示节点 ui 和 vi 之间有一条边。

请你构造一个二维矩阵，满足以下条件：

矩阵中每个格子 一一对应 图中 0 到 n - 1 的所有节点。
矩阵中两个格子相邻（横的或者竖的）当且仅当 它们对应的节点在 edges 中有边连接。

题目保证 edges 可以构造一个满足上述条件的二维矩阵。

请你返回一个符合上述要求的二维整数数组，如果存在多种答案，返回任意一个。

示例 1：

输入：n = 4, edges = [[0,1],[0,2],[1,3],[2,3]]

输出：[[3,1],[2,0]]

解释：

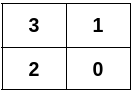
示例 2：

输入：n = 5, edges = [[0,1],[1,3],[2,3],[2,4]]

输出：[[4,2,3,1,0]]

解释：

示例 3：

输入：n = 9, edges = [[0,1],[0,4],[0,5],[1,7],[2,3],[2,4],[2,5],[3,6],[4,6],[4,7],[6,8],[7,8]]

输出：[[8,6,3],[7,4,2],[1,0,5]]

解释：

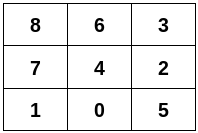
提示：

2 <= n <= 5 * 10^4
1 <= edges.length <= 10^5
edges[i] = [ui, vi]
0 <= ui < vi < n
树中的边互不相同。
输入保证 edges 可以形成一个符合上述条件的二维矩阵。

思路：拼图怎么玩？回想一下怎么玩拼图。拼图的最外圈是比较容易完成的：

先找角：找有两条直边的拼图块。
再找边：找有一条直边的拼图块。
我们可以先把第一排拼好，然后再考虑和第一排相关的拼图，依此类推。

总体思路：构造答案的第一行。根据第一行的元素，构造下一行，依此类推，直到最后一行。
构造答案的第一行

建图，然后把度数相同的点分到同一组。

分类讨论：

如果最小度数是 1，类似示例 2，答案只有一列。选其中一个度数为 1 的点，作为第一行。
如果不存在度数为 4 的点，类似示例 1，答案只有两列。选其中一个度数为 2 的点 x，以及 x 的一个度数为 2 的邻居 y，作为第一行。
否则，答案至少有三列。从其中一个度数为 2 的点（拼图的角）开始，不断寻找度数等于 3 的点（拼图的边），直到找到度数为 2 的点（拼图的另一个角）为止。把遇到的点按顺序作为第一行。
代码实现时，每种度数只需要知道一个点就够了。

构造其余行
设第一行的长度为 k，那么答案有n/k行。

用一个布尔数组 vis 标记已经填入的数字。

遍历当前行中的元素 x，由于 x 的上左右的数字都被标记了，如果 x 的邻居 y 没有被标记过，那么 y 就在 x 的正下方。把 y 加到下一行中。

如此迭代，循环 n/k-1次后构造完毕。

class Solution {
    public int[][] constructGridLayout(int n, int[][] edges) {
        List<Integer>[] g = new ArrayList[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int[] e : edges) {
            int x = e[0];
            int y = e[1];
            g[x].add(y);
            g[y].add(x);
        }

        // 每种度数选一个点
        int[] degToNode = new int[5];
        Arrays.fill(degToNode, -1);
        for (int x = 0; x < n; x++) {
            degToNode[g[x].size()] = x;
        }

        List<Integer> row = new ArrayList<>();
        if (degToNode[1] != -1) {
            // 答案只有一列
            row.add(degToNode[1]);
        } else if (degToNode[4] == -1) {
            // 答案只有两列
            int x = degToNode[2];
            for (int y : g[x]) {
                if (g[y].size() == 2) {
                    row.add(x);
                    row.add(y);
                    break;
                }
            }
        } else {
            // 答案至少有三列
            // 寻找度数为 2333...32 的序列作为第一排
            int x = degToNode[2];
            row.add(x);
            int pre = x;
            x = g[x].get(0);
            while (g[x].size() == 3) {
                row.add(x);
                for (int y : g[x]) {
                    if (y != pre && g[y].size() < 4) {
                        pre = x;
                        x = y;
                        break;
                    }
                }
            }
            row.add(x); // x 的度数是 2
        }

        int k = row.size();
        int[][] ans = new int[n / k][k];
        boolean[] vis = new boolean[n];
        for (int j = 0; j < k; j++) {
            int x = row.get(j);
            ans[0][j] = x;
            vis[x] = true;
        }
        for (int i = 1; i < ans.length; i++) {
            for (int j = 0; j < k; j++) {
                for (int y : g[ans[i - 1][j]]) {
                    // 上左右的邻居都访问过了，没访问过的邻居只会在下面
                    if (!vis[y]) {
                        vis[y] = true;
                        ans[i][j] = y;
                        break;
                    }
                }
            }
        }
        return ans;
    }
}

3312. 查询排序后的最大公约数

给你一个长度为 n 的整数数组 nums 和一个整数数组 queries 。

gcdPairs 表示数组 nums 中所有满足 0 <= i < j < n 的数对 (nums[i], nums[j]) 的最大公约数升序排列构成的数组。

对于每个查询 queries[i] ，你需要找到 gcdPairs 中下标为 queries[i] 的元素。请你返回一个整数数组 answer ，其中 answer[i] 是 gcdPairs[queries[i]] 的值。gcd(a, b) 表示 a 和 b 的 最大公约数 。

示例 1：

输入：nums = [2,3,4], queries = [0,2,2]

输出：[1,2,2]

解释：

gcdPairs = [gcd(nums[0], nums[1]), gcd(nums[0], nums[2]), gcd(nums[1], nums[2])] = [1, 2, 1].

升序排序后得到 gcdPairs = [1, 1, 2] 。

所以答案为 [gcdPairs[queries[0]], gcdPairs[queries[1]], gcdPairs[queries[2]]] = [1, 2, 2] 。

示例 2：

输入：nums = [4,4,2,1], queries = [5,3,1,0]

输出：[4,2,1,1]

解释：

gcdPairs 升序排序后得到 [1, 1, 1, 2, 2, 4] 。

示例 3：

输入：nums = [2,2], queries = [0,0]

输出：[2,2]

解释：

gcdPairs = [2] 。

提示：

2 <= n == nums.length <= 10^5
1 <= nums[i] <= 5 * 10^4
1 <= queries.length <= 10^5
0 <= queries[i] < n * (n - 1) / 2

思路：每个 GCD 的出现次数
直接把每个 GCD 出现多少次计算出来，这样就方便回答询问了。

如何计算 GCD 等于 2 的数对个数？

统计 nums 中的 2 的倍数的个数，假设有 5 个。那么我们可以从这 5 个数中选 2 个数，得到 $C_{5}^{2}$ =10个数对, 但这 10 个数对，每个数对的 GCD 并不一定都是 2，比如 8 和 12 的 GCD 是 4。

只能说，这 10 个数对的 GCD 都是 2 的倍数。

我们可以从 10 中减去 GCD 等于 4,6,8,⋯ 的数对个数，就得到 GCD 恰好等于 2 的数对个数了。

一般地，定义 cntGcd[i] 为 GCD 等于 i 的数对个数。枚举 i 的倍数，统计 nums 中有多少个数等于 i,2i,3i,⋯，记作 c。这 c 个数选 2 个数，组成 c(c-1)/2个数对。

但是，这些数对的 GCD 只是 i 的倍数，并不一定恰好等于 i。

减去其中 GCD 等于 2i,3i,⋯ 的数对个数，得cntGcd[i]= c(c−1)/2−cntGcd[2i]−cntGcd[3i]−⋯
为了完成这一计算，需要倒序枚举 i。

回答询问
比如 gcdPairs=[1,1,2,2,3,3,3]，对应的 gcdCnt=[0,2,2,3]，计算其前缀和，得 s=[0,2,4,7]。

q=0,1，答案都是 s 中的大于 q 的第一个数的下标，即 1。
q=2,3，答案都是 s 中的大于 q 的第一个数的下标，即 2。
q=4,5,6，答案都是 s 中的大于 q 的第一个数的下标，即 3。
所以在 s 中二分查找大于 q 的第一个数的下标即可。

代码：

class Solution {
    public int[] gcdValues(int[] nums, long[] queries) {
        int mx = 0;
        for (int x : nums) {
            mx = Math.max(mx, x);
        }
        int[] cntX = new int[mx + 1];
        for (int x : nums) {
            cntX[x]++;
        }

        long[] cntGcd = new long[mx + 1];
        for (int i = mx; i > 0; i--) {
            int c = 0;
            for (int j = i; j <= mx; j += i) {
                c += cntX[j];
                cntGcd[i] -= cntGcd[j]; // gcd 是 2i,3i,4i,... 的数对不能统计进来
            }
            cntGcd[i] += (long) c * (c - 1) / 2; // c 个数选 2 个，组成 c*(c-1)/2 个数对
        }

        for (int i = 2; i <= mx; i++) {
            cntGcd[i] += cntGcd[i - 1]; // 原地求前缀和
        }

        int[] ans = new int[queries.length];
        for (int i = 0; i < queries.length; i++) {
            ans[i] = upperBound(cntGcd, queries[i]);
        }
        return ans;
    }

    private int upperBound(long[] nums, long target) {
        int left = -1, right = nums.length; // 开区间 (left, right)
        while (left + 1 < right) { // 区间不为空
            // 循环不变量：
            // nums[left] <= target
            // nums[right] > target
            int mid = (left + right) >>> 1;
            if (nums[mid] > target) {
                right = mid; // 二分范围缩小到 (left, mid)
            } else {
                left = mid; // 二分范围缩小到 (mid, right)
            }
        }
        return right;
    }
}