冒泡，快排

问题提出

 请按从低到高的顺序排列下面的数据

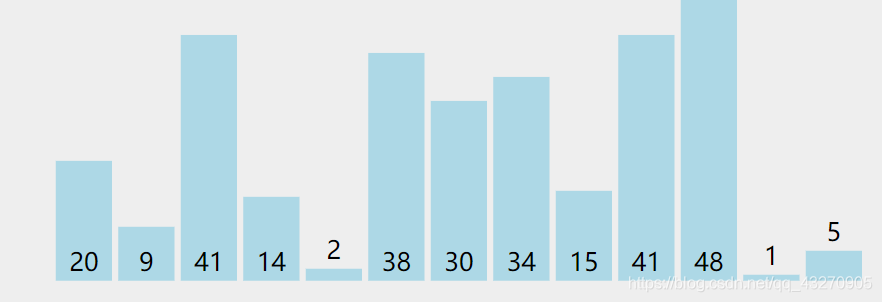
简单排序

 我们先不去考虑所谓的算法，如果要对这一系列的数进行排序的话，你会怎么拍？首先不难想到的是我们可以先找到最小的数，然后把它放在前面。那么对于机器而言，我们要如何呢？我们可以每次都可以找到最小的数，然后把它放到我们创建的新的数组里面，这样的话空间复杂度是O(n+1)（+1是指在配对时存取值的临时变量），时间复杂度为O（n^2）。
 紧接着我们去想一些优化的方法，首先我们可以意识到已经排好序的数我们就没有再次进行排序的必要了，因此就这一点我们可以想到，每次把最大的值移动到最后，然后再用同样的方法排前面的那几个数不就行了吗？也就是说我们现在的目的就是让最大的数到最后面去。于是怎么办呢？我们可采取一个临时的变量，然后用他记录下最大的数的下标，最后直接互换最后一个数与该数的位置即可。那么接着想，上面做法的缺点是什么？每次只有最后一个数和最大数进行了变换，这样有什么缺点呢？缺点在于临时数组的赋值操作会重复，就是说最大数前面仍不是理想状态。（举个例子来说，上图经过第一次循环后5 和 48 互换位置，进行第二次循环的时候临时变量要先存20的再存41的以此类推的进行赋值操作，可是如果我们在第一次变换的时候就调整了顺序呢？这样可以减小一部分的赋值操作）。这么想的话，每样比较的话不就成了相邻元素之间比较然后后一个是大的元素了吗？就是说我们可以不需要临时变量来存储了。
 我们可以用下面的方式互换:

void swap_add(int &a, int &b)
{
	a = a + b;
	b = a - b; 
	a = a - b;
}

 没错，这就是所谓的冒泡排序

基于分治的排序

 分治就是把一个大问题化成若干个小问题，然后依次解决。对于排序而言我们怎么把它化成小的问题呢？我们要是能把它们一分为二就好了，然后再用同样的法则分下去。可是分成两半的标准是什么呢？很明显，对于排序而言，他们的分界点应该是个中间值。于是乎问题成了去寻找中间值。这里有个很重要的一点是不要被两半限制了思维，这两半可以是长度不一样的啊。所以我们可以规定一个数值，划分的结果就是这个数值的左边小于这个数值右边大于这个数值。
 “中间值”找到了，接下来的问题是如何把它放到“中间”呢？没错，我们还是可以建立一个临时数组，然后小于中间值的放在前面，大的放在后面想想都麻烦。除了这个办法之外我们好有什么好的办法吗？这里还得稍微的转换一下思维，现在的要求是左边的数向往右边来，右边的数想往左边去。这样的话左右的数换一下不就好了吗？于是我们可以采取的方案是从最左边开始找到不满足小于“中间值”的数，然后记录下他的下标，然后就从右边开始找到不满足大于“中间值”的数，然后记录下来，然后再互换他们的位置即可。这样两个数就都满足了条件，接下俩继续往中间靠拢直到他俩相邻为止。这样就把“中间值”放到了指定的位置，并且我们还有了它的下标。然后分成的两个小的部分继续按上面的方法进行。没错，这就是快排。
 对于一个n个数据的数组而言，他能分为 $\log n$ 个小部分，对于每个部分而言，都要进行从两边到中间复杂度为O(n)的搜素。总共的时间复杂度为$n\log n$
 个人认为快排 = 分治 + 双指针
 算法，最厉害的是他的思维
 
 
 
 
 第一次写博客,不足、理解不周之处还望指出 (# ^ . ^ #)