动态规划——LCS最长公共子序列

提交VS地址
很早之前看过LCS但是热身赛却没写出来，枯了可能对dp还是存在疑惑，比赛中想到了一个奇特的思路，虽然Wa了但是对我个人来说意义不同，先说下DP的思路，看了网上以为Dalao的博客之后瞬间明白了 摘自https://www.cnblogs.com/wkfvawl/p/9362287.html
一，问题描述

给定两个字符串，求解这两个字符串的最长公共子序列（Longest Common Sequence）。比如字符串1：BDCABA；字符串2：ABCBDAB

则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA

二，算法求解

这是一个动态规划的题目。对于可用动态规划求解的问题，一般有两个特征：①最优子结构；②重叠子问题

①最优子结构

设 X=(x1,x2,…xn) 和 Y={y1,y2,…ym} 是两个序列，将 X 和 Y 的最长公共子序列记为LCS(X,Y)

找出LCS(X,Y)就是一个最优化问题。因为，我们需要找到X 和 Y中最长的那个公共子序列。而要找X 和 Y的LCS，首先考虑X的最后一个元素和Y的最后一个元素。

1）如果 xn=ym，即X的最后一个元素与Y的最后一个元素相同，这说明该元素一定位于公共子序列中。因此，现在只需要找：LCS(Xn-1，Ym-1)

LCS(Xn-1，Ym-1)就是原问题的一个子问题。为什么叫子问题？因为它的规模比原问题小。（小一个元素也是小嘛…）

为什么是最优的子问题？因为我们要找的是Xn-1 和 Ym-1 的最长公共子序列啊。。。最长的！！！换句话说，就是最优的那个。（这里的最优就是最长的意思）

2）如果xn != ym，这下要麻烦一点，因为它产生了两个子问题：LCS(Xn-1，Ym) 和 LCS(Xn，Ym-1)

因为序列X 和 序列Y 的最后一个元素不相等嘛，那说明最后一个元素不可能是最长公共子序列中的元素嘛。（都不相等了，怎么公共嘛）。

LCS(Xn-1，Ym)表示：最长公共序列可以在(x1,x2,…x(n-1)) 和 (y1,y2,…yn)中找。

LCS(Xn，Ym-1)表示：最长公共序列可以在(x1,x2,…xn) 和 (y1,y2,…y(n-1))中找。

求解上面两个子问题，得到的公共子序列谁最长，那谁就是 LCS（X,Y）。用数学表示就是：

LCS=max{LCS(Xn-1，Ym)，LCS(Xn，Ym-1)}

由于条件 1) 和 2) 考虑到了所有可能的情况。因此，我们成功地把原问题 转化 成了 三个规模更小的子问题。

②重叠子问题

重叠子问题是啥？就是说原问题 转化 成子问题后， 子问题中有相同的问题。咦？我怎么没有发现上面的三个子问题中有相同的啊？？？？

OK，来看看，原问题是：LCS(X,Y)。子问题有 ❶LCS(Xn-1，Ym-1) ❷LCS(Xn-1，Ym) ❸LCS(Xn，Ym-1)

初一看，这三个子问题是不重叠的。可本质上它们是重叠的，因为它们只重叠了一大部分。举例：

第二个子问题：LCS(Xn-1，Ym) 就包含了：问题❶LCS(Xn-1，Ym-1)，为什么？

因为，当Xn-1 和 Ym 的最后一个元素不相同时，我们又需要将LCS(Xn-1，Ym)进行分解：分解成：LCS(Xn-1，Ym-1) 和 LCS(Xn-2，Ym)

也就是说：在子问题的继续分解中，有些问题是重叠的。

由于像LCS这样的问题，它具有重叠子问题的性质，因此：用递归来求解就太不划算了。因为采用递归，它重复地求解了子问题啊。而且注意哦，所有子问题加起来的个数 可是指数级的哦。。。。

这篇文章中就演示了一个递归求解重叠子问题的示例。

那么问题来了，你说用递归求解，有指数级个子问题，故时间复杂度是指数级。这指数级个子问题，难道用了动态规划，就变成多项式时间了？？

呵呵哒。。。。

关键是采用动态规划时，并不需要去一 一 计算那些重叠了的子问题。或者说：用了动态规划之后，有些子问题 是通过 “查表“ 直接得到的，而不是重新又计算一遍得到的。废话少说：举个例子吧！比如求Fib数列。关于Fib数列，可参考：

求fib(5)，分解成了两个子问题：fib(4) 和 fib(3)，求解fib(4) 和 fib(3)时，又分解了一系列的小问题…

从图中可以看出：根的左右子树：fib(4) 和 fib(3)下，是有很多重叠的！！！比如，对于 fib(2)，它就一共出现了三次。如果用递归来求解，fib(2)就会被计算三次，而用DP(Dynamic Programming)动态规划，则fib(2)只会计算一次，其他两次则是通过”查表“直接求得。而且，更关键的是：查找求得该问题的解之后，就不需要再继续去分解该问题了。而对于递归，是不断地将问题分解，直到分解为 基准问题(fib(1) 或者 fib(0))

说了这么多，还是要写下最长公共子序列的递归式才完整。借用网友的一张图吧：）

c[i,j]表示：(x1,x2…xi) 和 (y1,y2…yj) 的最长公共子序列的长度。（是长度哦，就是一个整数嘛）。公式的具体解释可参考《算法导论》动态规划章节

这张DP表很是重要，从中我们可以窥见最长公共子序列的来源，同时可以根据这张表打印出最长公共子序列的构成路径

最后谈下我对这个Dp思想的理解，我觉得虽然DP是在拿前面的子问题推后面的解但是理解的话从后面向前面比较容易理解。看最后一个位置及DP[n][m] //其中n代表第一个字符串Str1的长度，m代表第二个字符串Str2的长度。而Dp[n][m]就代表了最长公共子序列，这个位置可以由DP[n-1][m-1]的位置或者Dp[n][m-1]或者Dp[n-1][m]的得来。如果它前面这个位置具有共同的字符那么Dp[n][m]就等于Dp[n-1][m-1]+1;也就是Str[n-1]==Str[m-1]的时候 而如果它前面这个位置不同就有可能来源于Dp[n][m-1]或者Dp[n-1][m]中的最大值。那我们想一下怎么实现？

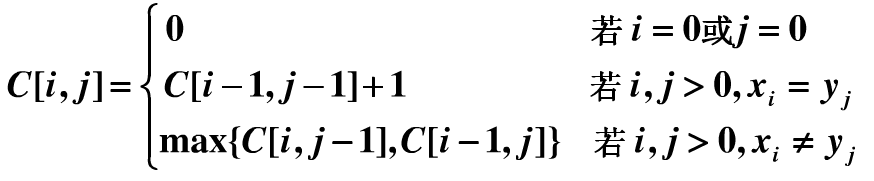
这张图就很形象的展示出了我们的思路，其实当我看到我代码的时候还有一个不明白之处就是为何两个循环遍历的下标都是从1开始的，后来想想是因为如果从0开始的话那么Dp[i-1][j-1]就越出了界限。其他的就很清楚的把我们的思路实现出来了。

/*

*/
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<string>
using namespace std;
const int maxn=1005;
int dp[maxn][maxn];
int main() 
{
	string  s1,s2; 
	while(cin>>s1>>s2){
		int len1=s1.size();
		int len2=s2.size();
		memset(dp,0,sizeof(dp)); 
		for(int i=1;i<=s1.size();i++) {
			for(int j=1;j<=s2.size();j++) {
				if(s1[i-1]==s2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
				else {
					dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
				}
			}
		}
		cout<<dp[len1][len2]<<endl;
	}
	return 0;
}

另外一个思路就是Wa了好多次的想法了虽然说最后知道自己哪里出错了但是很开心能够想到这种方法。也可以说运用了简单的哈希，其实我现在对哈希并不是能灵活运用，只知道它是把字符串的一些处理转成了int型数据进行了处理，这个题的话我的思路是把每个字符串的字符对应的Ascll码值都当成数组的下标而它里面放的数据就是这个字符在字符串中的位置。比如题中的样例
abcfbc 及num1[97]=1,num1[98]=2…等等，然后第二个字符串也用相同的方法存放下标及
abfcab及num2[97]=1,num2[98]=2…等等。
然后我们用两个for循环拿第一个字符串中的字符在第二个字符串中寻找看是否有相对应的位置信息，及用i代表第一个字符串的第一个元素的下标,开一个变量记录对应字符的Ascll值及k=str[i]然后如果num2[k]>0并且要取前面一个字符及qk=str[i-1]如果num2[k]>num[qk]就证明这个字符可以假如到公共子序列中，可是有一个致命的错误就是这样无法应对当字符串有重复字母的时候怎么选择比如两个字符串 11111 和11 无论怎么更新位置，num1[1]存放的只能是一个位置，所以这也是一直Wa’的原因，不过这个思路也算是我原来思路的突破了。
能过样例的代码

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<string>
using namespace std;
int main()
{
	string s1,s2;
	while(cin>>s1>>s2){
		int num[1005]={0},num1[1005]={0};
	for(int i=0;i<s2.size();i++) {
		int k=s2[i];
		if(!num[k])  num[k]=i+1;
	}
	for(int i=0;i<s1.size();i++) {
		int k=s1[i];
		if(!num1[k]) num1[k]=i+1;
	}
	int cnt=0,sum=0,sum1=0;
	for(int i=0;i<s1.size();i++) {
		int k=s1[i];
		if(num[k]) {
		   int j;
		   j=i+1;
		   cnt=1;
		   while(1) {
		   	if(j>s1.size()) break;
		   	  k=s1[j];
		   	  int p=s1[j-1];
		   	  if(num[k]>num[p]) cnt++;
		   	  j++;
		   }
		   sum=max(sum,cnt);	
		}
	}
	for(int i=0;i<s2.size();i++) {
		int k=s2[i];
		if(num1[k]) {
		   int j;
		   j=i+1;
		   cnt=1;
		   while(1) {
		   	if(j>s2.size()) break;
		   	  k=s2[j];
		   	  int p=s2[j-1];
		   	  if(num1[k]>num1[p]) cnt++;
		   	  j++;
		   }
		   sum1=max(sum1,cnt);	
		}
	}
	cout<<max(sum,sum1)<<endl;
}
}