数学建模方法—【07】灰色预测GM(1,1)

灰色预测GM(1,1)

1. 概念:

系统	说明
白色系统	系统的信息完全明确，没有缺少等问题
灰色系统	系统的部分信息已知，部分信息未知。
黑色系统	系统的内部信息是未知的

灰色预测: 对既含有已知信息又含有不确定信息的系统进行预测，就是对在一定范围内变化的、与时间有关的灰色过程进行预测的预测方法。

2. GM(1,1)模型

G：Gray
M：Model
第一个1：表示微分方程是一阶的
第二个1：表示只有一个自变量
    GM(1,1)是使用原始的离散非负数据列，通过一次累加生成削弱随机性的较有规律的新的离散数据列，然后通过建立微分方程模型，得到在离散点处的解经过累减生成的原始数据的近似估计值，从而预测原始数据的后续发展。

3. 原理

    设$x^0=(x^0(1),x^0(2),x^0(3),...,x^0(n))$是最初的非负数据列，对其进行一次累加，得到新的生成的数据列$x^{(1)}(x^{(0)}的1-AGO序列，AGO:AccumulatingGenerationOperator)$：
$$x^{(1)}=(x^{(1)}(1),x^{(1)}(2),...,x^{(1)}(n))$$
其中$x^{(1)}(m)=\sum _{i=1}^m{x}^{(0)}(i),m=1,2...,n$
    令$z^{(1)}$为数列$x^{(1)}$的紧邻均值生成数列，即
$$z^{(1)}=(z^{(1)}(2),z^{(1)}(3),...,z^{(1)}(n))$$
其中，$z^{(1)}(m)=\delta x^{(1)}(m)+(1-\delta )x^{(1)}(m-1),m=2,3,...,n且\delta 一般为0.5$
举例:

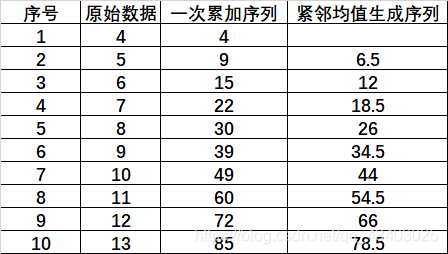
    一般情况下，称$x^{(0)}(k)+a{z}^{(1)}(k)=b$为$GM(1,1)$的基本形式$(k=2,3,...,n)$,其中b表示灰作用量，-a表示发展系数。
引入矩阵形式:
$$u=(a,b{)}^T,Y=\left[\begin{array}{c}{x}^0(2)\\ x^0(3)\\ ....\\ x^0(n)\end{array}\right],B=\left[\begin{array}{cc}-z^1(2)& 1\\ -z^1(3)& 1\\ ...& ...\\ -z^1(n)& 1\end{array}\right]$$
所以$x^{(0)}(k)+a{z}^{(1)}(k)=b$可以表示为$$Y=Bu$$
$x^{(0)}(k)+a{z}^{(1)}(k)=b$可以表示为$$x^{(0)}(k)=b-a{z}^{(1)}(k)$$该式子可以看为一次函数的形式$y=kx+b$,所以可以根据OLS最小二乘法，得到参数a,b的估计值为(最小二乘法请读者自行查询理解):
$$\hat{u}=\left(\genfrac{}{}{0ex}{}{\hat{a}}{\hat{b}}\right)=(B^{T}B{)}^{-1}{B}^{T}Y$$
得到$\hat{a}和\hat{b}$后，便可得
$$x^{(0)}(k)=\hat{b}-\hat{a}{z}^{(1)}(k),k=2,3,...,n$$
又因为
$$x^{(0)}(k)=x^{(1)}(k)-x^{(1)}(k-1)$$
so
$$x^{(1)}(k)-x^{(1)}(k-1)=\hat{b}-\hat{a}{z}^{(1)}(k)$$
根据牛顿-莱布尼茨公式可得:
$$x^{(1)}(k)-x^{(1)}(k-1)={\int }_{k-1}^k\frac{d{x}^{(1)}(t)}{dt}dt$$
又因为$z^{(1)}(m)=0.5x^{(1)}(m)+0.5x^{(1)}(m-1)$即$z^{(1)}(k)=\frac{x^{(1)}(k-1)+x^{(1)}(k)}{2}$
则根据定积分的几何意义可得:
$$z^{(1)}(k)=\frac{x^{(1)}(k-1)+x^{(1)}(k)}{2}={\int }_{k-1}^k{x}^{(1)}(t)dt$$
整理得到:
$${\int }_{k-1}^k\frac{d{x}^{(1)}(t)}{dt}dt=-\hat{a}{\int }_{k-1}^k{x}^{(1)}(t)dt-{\int }_{k-1}^k\hat{b}dt={\int }_{k-1}^k[\hat{b}-\hat{a}{x}^{(1)}(t)]dt$$
可得GM(1,1)的白化方程：
$$\frac{d{x}^{(1)}(t)}{dt}=\hat{b}-\hat{a}{x}^{(1)}(t)$$
再对白化方程进行研究(中间过程省略)，可得出GM(1,1)模型的本质是有条件的指数拟合:
$$f(x)=C_1{e}^{c_2(x-1)}$$
所以数据具有准指数规律是使用灰色系统建模的理论基础,即数据具有准指数规律是使用GM(1,1)模型的前提！！！！

4. 使用GM(1,1)的步骤

1. 准指数规律的检验:

序列$x^{(0)}$的级比$$\lambda (k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,3,...,n$$
若所有的级比都落在区间 $(e^{\frac{-2}{n+1}},e^{\frac{2}{n+1}})$内，则数列 x(0)可以利用GM(1,1)模型进行灰色预测。否则，对数据做适当的变换处理，如平移变换：
$$y^{(0)}(k)=x^{(0)}(k)+c,k=1,2,...,n$$
取合适的c使得数据列的级比都落在区间 $(e^{\frac{-2}{n+1}},e^{\frac{2}{n+1}})$内！

2. 建立GM(1,1)模型

根据原理先获得1-AGO:

$$x^{(1)}=(x^{(1)}(1),x^{(1)}(2),...,x^{(1)}(n))$$
其中$x^{(1)}(m)=\sum _{i=1}^m{x}^{(0)}(i),m=1,2...,n$
再得到紧邻均值生成数列
    令$z^{(1)}$为数列$x^{(1)}$的紧邻均值生成数列，即
$$z^{(1)}=(z^{(1)}(2),z^{(1)}(3),...,z^{(1)}(n))$$
其中，$z^{(1)}(k)=\frac{x^{(1)}(k-1)+x^{(1)}(k)}{2}$
再得到GM(1,1)的一般模型:
$$x^{(0)}(k)=b-a{z}^{(1)}(k)$$
再根据回归得到$\hat{a},\hat{b}$
可得GM(1,1)的白化方程：
$$\frac{d{x}^{(1)}(t)}{dt}+\hat{a}{x}^{(1)}(t)=\hat{b}$$
解得:
$$x^{(1)}(t)=(x^{(0)}(1)-\frac{b}{a})e^{-a(t-1)}+\frac{b}{a}$$
所以得到一次累加数列预测值:
$${\hat{x}}^{(1)}(k+1)=(x^{(0)}(1)-\frac{b}{a})e^{-ak}+\frac{b}{a},k=1,2,...,n-1$$
得到预测值为
$${\hat{x}}^{(0)}(k+1)={\hat{x}}^{(1)}(k+1)-{\hat{x}}^{(1)}(k),k=1,2,...,n-1$$
又因为
$${\hat{x}}^{(1)}(k+1)=(x^{(0)}(1)-\frac{b}{a})e^{-ak}+\frac{b}{a},k=1,2,...,n-1$$
$${\hat{x}}^{(1)}(k)=(x^{(0)}(1)-\frac{b}{a})e^{-a(k-1)}+\frac{b}{a},k=2,...,n-1$$
所以
$${\hat{x}}^{(0)}(k+1)={\hat{x}}^{(1)}(k+1)-{\hat{x}}^{(1)}(k)$$

  $=(x^{(0)}(1)-\frac{b}{a})e^{-ak}+\frac{b}{a}-(x^{(0)}(1)-\frac{b}{a})e^{-a(k-1)}+\frac{b}{a}$
  $=(x^{(0)}(1)-\frac{b}{a})(e^{-ak}-e^{-a(k-1)})$
  $=(x^{(0)}(1)-\frac{b}{a})\cdot e^{-ak}\cdot (1-e^a),k=1,2,...,n-1$

3. 模型评价

一般来说，GM(1,1)有2种评价方法，即评价模型对原数据的拟合程度或者还原程度:

1. 残差检验:
   $$绝对残差:\epsilon (k)=x^{(0)}(k)-{\hat{x}}^{(0)}(k),k=2,3,...,n$$
   $$相对残差:{\epsilon }_r(k)=\frac{|x^{(0)}(k)-{\hat{x}}^{(0)}(k)|}{x^{(0)}(k)}\times 100\%,k=2,3,...,n$$
   $$平均相对残差:\overline{{\epsilon }_r}=\frac{1}{n-1}\sum _{k=2}^n|{\epsilon }_r(k)|$$
   如果$\overline{{\epsilon }_r}<20\%$,则认为GM(1,1)对原数据的拟合达到一般要求；
   如果$\overline{{\epsilon }_r}<10\%$,则认为GM(1,1)对原数据的拟合效果非常不错；
2. 级比偏差检验:
   序列$x^{(0)}$的级比$$\lambda (k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,3,...,n$$
   再根据发展系数$-\hat{a}$计算出相应的级比偏差和平均级比偏差：
   $$级比偏差:\eta (k)=|1-\frac{1-0.5\hat{a}}{1+0.5\hat{a}}\frac{1}{\sigma (k)}|$$
   $$平均级比偏差:\overline{\eta }=\sum _{k=2}^n\frac{\eta (k)}{n-1}$$
   如果$\overline{\eta }<0.2$,则认为GM(1,1)对原数据的拟合达到一般要求；
   如果$\overline{\eta }<0.1$,则认为GM(1,1)对原数据的拟合效果非常不错；

5. 代码

'''
author: Blue
time: 2020.11.10
e-mail: 2458682080@qq.com
'''
#!/usr/bin/env python
# coding: utf-8

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
import matplotlib



class GrayForecast():
    # 初始化
    def __init__(self, data):
        self.data = data    # 以列表的形式传入待预测数据
        self.forecast_list = self.data.copy()   # 把待预测数据复制一份

 
   # 数据级比校验
    def level_check(self): 
        n = len(self.data)
        lambda_k = np.zeros(n-1)
        # 计算序列的级比
        for i in range(n-1):
            lambda_k[i] = self.data[i]/self.data[i+1]
            if lambda_k[i] < np.exp(-2/(n+1)) or lambda_k[i] > np.exp(2/(n+2)):
                flag = False
            else:
                flag = True

        self.lambda_k = lambda_k
        if not flag:
            print("级比校验失败，请对X(0)做平移变换！！")
            return False
        else:
            print("级比校验成功，继续执行！！")
            return True
 

    # GM(1,1)建模
    def GM_11_model(self, data_to_use=10):
    # data_to_use是指你要用多少数据去预测下一个数据，这里用10个
        if data_to_use > len(self.data):
            raise Exception('您的数据行不够')
        # 把待预测数据中要用于预测下一个数据的数据取出来
        X_0 = np.array(self.forecast_list[len(self.forecast_list)-data_to_use:len(self.forecast_list)])
        
        # 1-AGO 获得一次累加值
        X_1 = np.zeros(X_0.shape)
        for i in range(X_0.shape[0]):
            X_1[i] = np.sum(X_0[0:i+1])
            
        # 紧邻均值生成序列
        Z_1 = np.zeros(X_1.shape[0]-1)
        for i in range(1, X_1.shape[0]):
            Z_1[i-1] = -0.5*(X_1[i]+X_1[i-1])
        
        # 计算a,b
        B = np.append(np.array(np.mat(Z_1).T), np.ones(Z_1.shape).reshape((Z_1.shape[0], 1)), axis=1)
        Yn = X_0[1:].reshape((X_0[1:].shape[0], 1))

        B = np.mat(B)
        a_ = (B.T*B)**-1 * B.T * Yn
        a, b = np.array(a_.T)[0]
        X_ = np.zeros(X_0.shape[0])
        def f(k):
            x1_pre = (X_0[0]-b/a) * np.exp(-a*(k)) + b/a
            x0_pre = (X_0[0]-b/a)*(1-np.exp(a))*np.exp(-a*(k))
            return x0_pre
            
        # 调用函数f进行预测
        # 先对原始数据进行
        self.forecast_list.append(round(f(X_.shape[0]), 2))  


    # 调用模型进行预测
    def forecast(self, time):  # time是指你要预测几次，即预测几个值
        for i in range(time):
            self.GM_11_model()
        return self.forecast_list


    # 得到原始数据的预测数据(即拟合数据)
    def fit(self, data_all_len, data_to_use=10):  
        if data_to_use > len(self.data):
            raise Exception('您的数据行不够')
        X_0 = np.array(self.forecast_list[len(self.forecast_list) - data_to_use:len(self.forecast_list)])
        X_1 = np.zeros(X_0.shape)
        for i in range(X_0.shape[0]):
            X_1[i] = np.sum(X_0[0:i + 1])

        Z_1 = np.zeros(X_1.shape[0] - 1)
        for i in range(1, X_1.shape[0]):
            Z_1[i - 1] = -0.5 * (X_1[i] + X_1[i - 1])

        B = np.append(np.array(np.mat(Z_1).T), np.ones(Z_1.shape).reshape((Z_1.shape[0], 1)), axis=1)
        Yn = X_0[1:].reshape((X_0[1:].shape[0], 1))

        B = np.mat(B)
        a_ = (B.T * B) ** -1 * B.T * Yn
        a, b = np.array(a_.T)[0]
        X_ = np.zeros(X_0.shape[0])
        fit_list = [self.data[0]]
        def f(k):
            x1_pre = (X_0[0] - b / a) * np.exp(-a * (k)) + b / a
            x0_pre = (X_0[0] - b / a) * (1 - np.exp(a)) * np.exp(-a * (k))
            return x0_pre
            
        # 根据原始数据的长度，对原始数据进行预测
        # 因为原理解释时，序列下标从1开始，但是算法下标是从0开始的，所以算法这边和原理是有一点不一样的
        for g in range(0, data_all_len-1):   # 1,2,...,n-1
            fit_list.append(round(f(g),2))  
        return fit_list

类写好后，就可以调用了！这里我用一次数学建模的数据为例，数据描述的是小龙虾的数量:

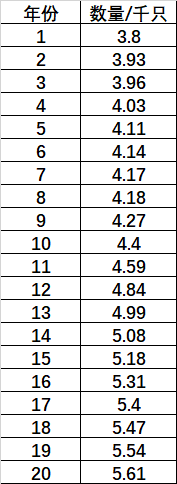
longxia = [3.8, 3.93, 3.96, 4.03, 4.11, 4.14, 4.17, 4.18, 4.27, 4.4, 4.59, 4.84, 4.99, 5.08, 5.18, 5.31, 5.4, 5.47, 5.54, 5.61]
if __name__=='__main__':
    data_len = len(longxia)
    gf = GrayForecast(longxia)
    # 先级比校验
    gf.level_check()
    # 预测后10年的小龙虾数量
    forecast_data = gf.forecast(10)
    
    # 将残差转换为字符串
    res_list_str = []
    # 用于存放每对相应的值计算出来的残差
    res_list = []
    # 得到20个原始值的拟合值
    fit_data = gf.fit(20)
    
    # 计算相对残差
    for h in range(1, data_len): 
        res = round(abs((forecast_data[h] - fit_data[h]) / forecast_data[h]),4)
        res_list.append(res)
        res_str = str(round(abs((forecast_data[h] - fit_data[h]) / forecast_data[h]),4)*100) + '%'
        res_list_str.append(res_str)
        
    # 平均相对残差
    res_sum = 0
    for index in range(data_len-1):
        res_sum += res_list[index]
    res_aver = res_sum / (data_len - 1)
    
    print('原始值+预测值为:', forecast_data)
    print('拟合值为:',fit_data)
    print('相对残差为:',res_list_str)
    print('平均相对残差为:', (str(round(res_aver,4) * 100)+'%'))
    # 日期
    date = [i for i in range(1,data_len+1)]

        date = [i for i in range(1,data_len+1)]
    date_ = [k for k in range(data_len, len(forecast_data)+1)]

    # 作图
    plt.figure()
    plt.plot(date,fit_data, label='拟合值',color='#019529', marker="d")
    plt.plot(date, forecast_data[0:data_len],color="#cea2fd", label='实际值',marker='*')
    plt.plot(date_, forecast_data[data_len-1:len(forecast_data)],color="#0bf9ea", label='预测值',marker='X')
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
    plt.title('小龙虾数量预测图')
    plt.legend()  # 显示图例fontsize=20
    plt.show()
    plt.savefig(r'C:\Users\Yunger_Blue\Desktop\小龙虾')

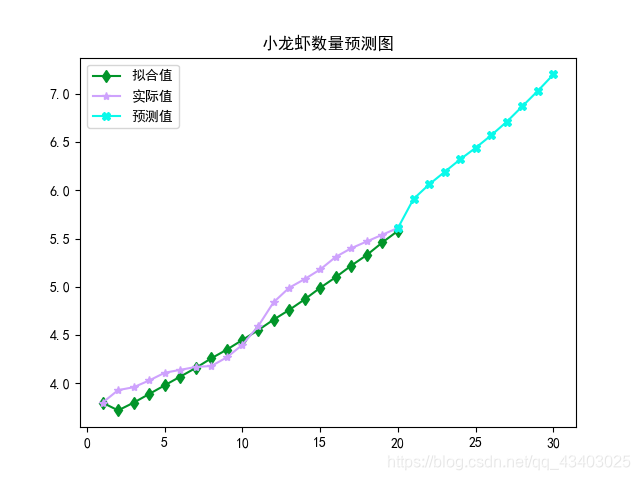
结果为:

级比校验成功，继续执行！！
实际值为: [3.8, 3.93, 3.96, 4.03, 4.11, 4.14, 4.17, 4.18, 4.27, 4.4, 4.59, 4.84, 4.99, 5.08, 5.18, 5.31, 5.4, 5.47, 5.54, 5.61, 5.91, 6.06, 6.19, 6.32, 6.44, 6.57, 6.71, 6.87, 7.03, 7.2]
预测值为: [3.8, 3.72, 3.8, 3.89, 3.98, 4.07, 4.16, 4.26, 4.35, 4.45, 4.55, 4.66, 4.76, 4.87, 4.99, 5.1, 5.22, 5.33, 5.46, 5.58]
相对残差为: ['5.34%', '4.04%', '3.47%', '3.16%', '1.69%', '0.24%', '1.91%', '1.87%', '1.1400000000000001%', '0.8699999999999999%', '3.7199999999999998%', '4.61%', '4.130000000000001%', '3.6700000000000004%', '3.95%', '3.3300000000000005%', '2.56%', '1.44%', '0.53%']

结果图为: