用Floyd和Dijkstra算法计算最短路径问题

1.Floyd算法介绍

1.算法特点：

弗洛伊德算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或有向图或负权（但不可存在负权回路)的最短路径问题，同时也被用于计算有向图的传递闭包。

2.基本思想：
对于从vi到vj的弧，进行n次试探：首先考虑路径vi,v0,vj是否存在，如果存在，则比较vi,vj和vi,v0,vj的路径长度，取较短者为从vi到vj的中间顶点的序号不大于0的最短路径。在路径上再增加一个顶点v1，依此类推，在经过n次比较后，最后求得的必是从顶点vi到顶点vj的最短路径。

3.数据结构：
① 图的存储结构：带权的邻接矩阵存储结构 。
②数组dist[n][n]：存放在迭代过程中求得的最短路径长度。

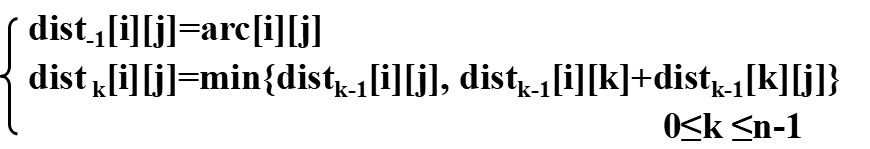
③数组path[n][n]：存放从vi到vj的最短路径，初始为path[i][j]=“vivj”。
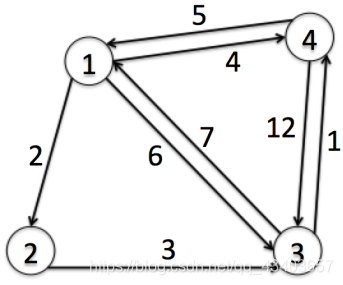
实例演示用Floyd算法求解下图各个顶点的最短距离。

解析
对于上述的旅行最短路径问题，首先我们需要初始化一个矩阵来储存图的信息。如下，横坐标表示起点，纵坐标表示终点，如e[1][2]表示从1号顶点到2号顶点的距离为2。其中，起点与终点相同时距离为0，无直达路径的初始化为无穷大（在实际中这个值只要大于最大路径之和即可），如e[3][2]=∞。

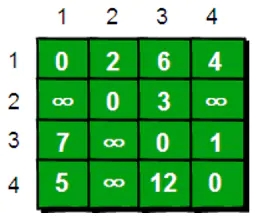
现在我们得到了各个直达顶点之间的距离图，但是直达有时并不能表示他就是最近的，例如从1号到3号直达距离为6，但是经过2作为中转站后距离缩短为5。因此我们需要计算出任意两个顶点之间的最短距离就需要将中转这种情况考虑进去。
首先我们仅考虑允许使用1号顶点作为中间点的情况来更新这个距离表。我们可以将城市之间的有向边看做向量来相加，这样可能更好理解。比如begin表示起点，end表示终点那么向量[begin][end]=[begin][1]+[1][end]。以1号作为中间点更新距离的代码为：

#m表示初始矩阵
#这里i表示对起点的遍历
for i in range(4):
    #这里j表示对终点的遍历
    #因此m[i][j]就表示遍历了所有的顶点
    for j in range(4):
        update = m[i][1]+m[1][j]
        if m[i][j] > update:
            #直达的值小于经过了1号中间点的值则更新距离矩阵
            m[i][j]=update

更新结果

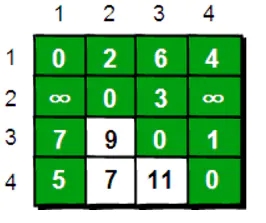
同理，我们可以在1号的基础上更新其余顶点的最短路径，代码如下:

#k表示作为中间点的顶点
for k in range(4):
    #i同样表示起点
    for i in range(4):
        #j表示终点
        for j in range(4):
            update = e[i][k]+e[k][j]
            if e[i][j]>update:
                e[i][j]=update

完整代码

#include<stdio.h>
int main()
{
   
    int e[10