【论文解读】谐波网络（Harmonic Network)

本文链接：https://blog.csdn.net/qq_43404360/article/details/134020137

【圆谐波】

圆谐波可以理解为谐波，其实就是正弦函数，只是两者所处的坐标系是不同的。大家都知道欧拉公式 $e^2=cos\theta+isin\theta$ ，这里的圆谐波其实就是正弦函数或者余弦函数在极坐标域上的表示。圆谐波具有以下的极坐标表达式形式：

$W_m(r,\phi;R,\beta)=R(r)e^{i(m\phi+\beta)}$

其中 $r$ 和 $\phi$ 是极坐标自变量， $R$ 表示一个只与极径 $r$ 相关函数， $e^{i(m\phi+\beta)}$ 是只与极角相关的函数， $\beta$ 是角常量偏置。这里给出复数高斯核的例子： $W_m(r,\phi';e^{-r^2},0)=e^{-r^2}e^{im\phi}$ 。这个圆谐波函数的图像如下所示。

【等变表示】

简单而言，等变表示或者等变特征是指，经由特征提取器（通常为某种神经网络，比如本文介绍的谐波网络）提取的特征保留了原始数据的方位和姿态信息。这与不变表示或者不变特征相对应，在不变特征中，则没有保留原始数据的方位和姿态信息。举个例子，如果针对猫的特征训练一个等变神经网络，当输入的猫发生旋转时，经由该网络所提取的特征，应该只发生与输入变换对应的变换。这里没有直接说是与输入相同的变换，是因为输入空间和输出空间可能不一样，相应变换的表现形式也可能不一样。但是输入变换和输出变换之间应该有明确的对应关系。

【谐波网络】

谐波网络的核心在于限制卷积核是圆谐波函数（的线性组合），能够将360度的连续的旋转等变性编码到特征表示中（即能够保持输入图片任意角度的旋转变换到提取的特征中），具体的推导见后，这里需要注意两点，一是这里的滤波器是复数滤波器，等下卷积得到的特征图也是复数特征图；二是滤波器是定义在极坐标下的，后面会提到怎样从极坐标域采样，得到像素滤波器（即常见的滤波器形式）。

在极坐标系上考虑一张图像（特征映射） $F(r,\phi)$ 。当图片关于原点进行旋转，则旋转后的图像记为 $F(r,\pi^{\theta}[\phi])=F(r,\phi-\theta)$ ，简记为 $F^\theta$ 。下面定义旋转互相关（rotational cross-correlation $\star$ ）操作为：

$[W_m\star F]=\int_{\phi}\int_{R}W_m(rR_\phi\widehat{x})F(rR_\phi\widehat{x})drd\phi$

对其中的符号进行一些说明：x表示直角坐标，记 $x=r\widehat{x}$ ，其中 $r=\left \| x \right \|_2\geq 0$ ，而 $\widehat{x}=(con\beta,sin\beta)$ 对应极坐标中角度的部分， $\beta=\angle\widehat{x}$ 。这个式子实际上就是互相关在极坐标的写法，它有一个很好的性质：

$[W_m\star F^\theta]=e^{im\theta}[W_m\star F^0]$

这实际上就说明这个旋转互相关操作对输入变换具有等变性，大家可以对照前文提到的等变表示的概念，也就能理解为什么前面说输出的变换不一定和输入的变换完全一样，但需要有对应关系。下面对这个等变性质进行证明。

$\begin{aligned} W_m\star R_\theta F & =\int_\Phi\int_R W_m(rR_\phi\hat{x}) F(rR_\phi R_{-\theta}\hat{x})drd\phi \\ &=\int_\Phi\int_R W_m(rR_\phi\hat{x})F(rR_{\phi-\theta}\hat{x})drd\phi \\ &=\int_{\Phi}\int_{R}W_m(rR_{\phi' + \theta}\widehat{x})F(rR_{\phi'}\widehat{x})drd\phi' \\ &=\int_{\Phi}\int_{R}R(r)e^{i(m(\phi'+\theta) + \beta)}F(rR_{\phi'}\widehat{x})drd\phi' \\ &=e^{im\theta}\int_{\Phi}\int_{R}R(r)e^{i(m\phi' + \beta)}F(rR_{\phi'}\widehat{x})drd\phi' \\ &=e^{im\theta}[W_m\star F] \end{aligned}$

这个证明的含义是，当输入的图片发生旋转后，所提取的特征就会乘上一个与输入图片的旋转角度相关的乘子 $e^{im\theta}$ ，这里的m反映了圆谐波滤波器的频率性质，称为滤波器的旋转阶，m通常可取多个值，不同的m会得到不同响应结果。下图显示了这个过程的等变性，由于响应结果与m相关，因此称为m等变映射（m-equivariant feature map)：

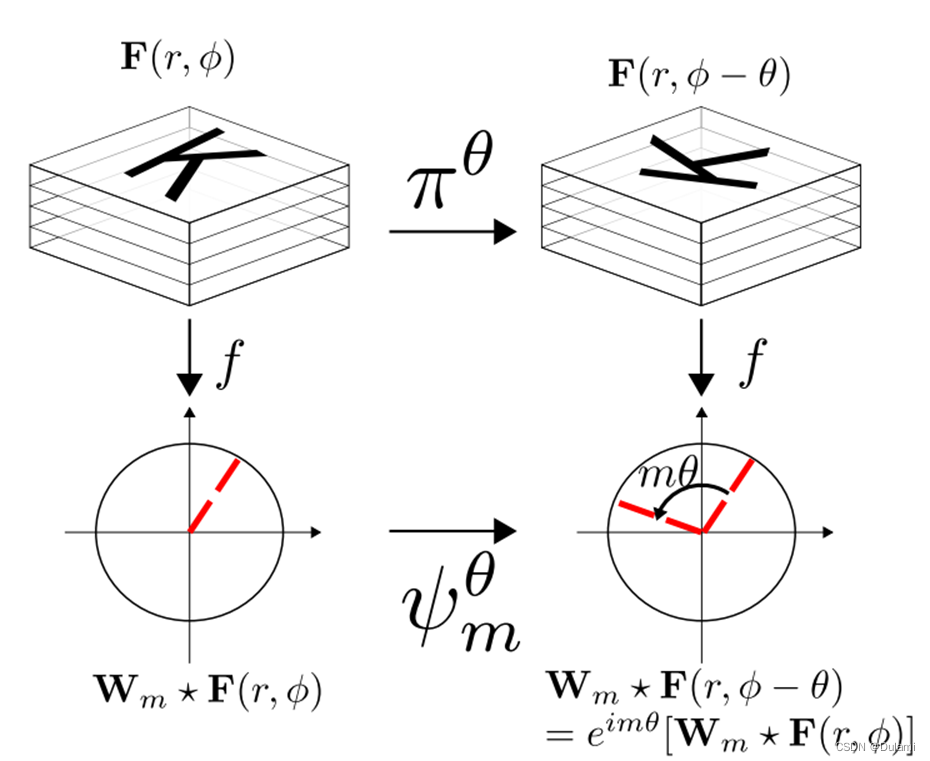
旋转等变性具有一些比较重要的性质：

链式互相关：输入图片的旋转阶（rotation order）是0阶，此后与m阶的滤波器卷积，将会得到旋转阶为m阶的特征图，如果输入特征的旋转阶是m，滤波器的旋转阶是n，则输出特征的旋转阶是𝑚+𝑛。

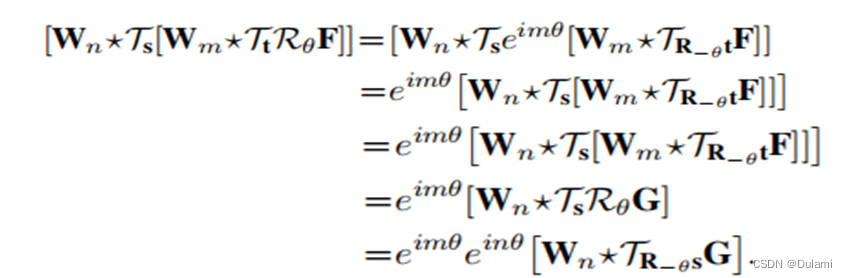
幅值（Magnitude）非线性：作用于幅值的非线性不影响旋转等变性。这个很好理解，因为旋转角度只与复指数有关，而幅值只与复指数的系数有关（即R(r))。

特征图相加：相同阶数的特征图可以相加，得到的新特征图的旋转阶不变。如果将复杂的特征与以不同频率旋转的相位相结合，会导致响应的纠缠。生成的特征图不再对单一旋转阶等变，很难使用。因此需要在每个特征图上强制保持阶数相等。这个条件对网络架构有影响。

前面提到，在提取特征的过程中会用到多个不同旋转阶的滤波器，相应也会有不同旋转阶的特征映射。为了避免特征图在叠加（或池化）后导致阶数混淆，亦即响应的纠缠（会导致后续的计算变复杂），作者提出将叠加的过程限制在固定的流（stream)上，在固定流上的特征图的旋转阶等于流的旋转阶。假如当前流的旋转阶是M，则以任意路径到达流的终点，都应当满足 $\sum_{i=0}^{l}m_i=M$ ，其中 $l$ 表示卷积层数。从不同路径得到的相同旋转阶的特征图可以叠加，叠加后的特征图旋转阶不变。网络最终只用了stream 0（即M = 0）的最终的特征图。

谐波网络的核心就是以圆谐波族函数为滤波器进行卷积（互相关），此外还有一些实现上的细节。一是复数互相关可以由四次实数互相关实现：

二是在池化层使用平均池化，不能使用最大池化，具体原因我没读懂，大家可以参考原文。

三是我们前面定义的滤波器是定义在极坐标系上的，而实际上的图片却处在直角坐标系，因此需要将极坐标滤波器采样为像素滤波器，原文使用的采样方法为高斯重采样，具体过程为：

确定像素滤波器的大小，假设为 $n\times n$ ，那么这个滤波器就有 $n^2$ 个点；
极坐标滤波器由若干圈（rings)采样组成，这里的采样是指角度采样，即固定角度间隔采样，由内到外每个圈的半径等差递增，最内圈的半径为0，向外逐层加1，圈数是n / 2，不过需要设置一个最小值，源代码设置为4。极坐标中每个点都有自己的值，从代码来看，每个点的值为： $W(r_j)=re^{-im\theta}, r_j=(r,\theta)$ ，这个值其实就是极坐标滤波器的每个点的权重，需要和下面的高斯权重相区分；
以像素滤波器的中心为原点，将两个坐标系重合。对于像素滤波器的每个点，计算该点到极坐标滤波器上所有点的高斯权重，将该高斯权重与每个极坐标点的值相乘再相加（加权求和），得到像素滤波器下该点的权重。