最短路径——贝尔曼-福特BelLnan-Ford算法详解与实现

7.5.2 弧上权值为任意值的单源点最短路径问题

弧上权值为任意值的单源点最短路径难点

1. 图一般的情况：带权有向图G上弧的权值可能为负值。对于带权有向图来说，利用上节给出的迪克斯特拉算法，不一定能得到正确的结果（带负权的回路最短路径是不存在的，可以一直循环下去）。若设源点V0=A，使用迪克斯特拉算法，显然，结果是有问题的。
   
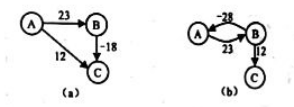
2. 为了能够求解弧上带有负权值的单源最短路径问题，贝尔曼（BelLnam）和福特（Ford）提出了从源点逐次经过其他顶点，以缩短到达终点的最短路径长度的方法。该方法有一个限制条件，即要求图中不能有路径长度为负值的回路。例如，图（b）中有一个回路（A，B，A），其路径长度为-5。当路径为（A,B,A,B,…,A,B,C）时，路径长度会越来越小，顶点A到顶点C的最短路径长度可达负无穷大。为了能够用有限条弧构成最短路径，必须把这种情况避开。所以在贝尔曼-福特算法中不考虑这种情况。
3. 当图中没有路径长度为负值的回路时，有n个顶点的图中任意两个顶点之间如果存在最短路径，此路径最多有n-1条弧。这是因为如果路径上的弧数超过了n-1条时，必然会重复经过一个顶点，形成路径长度为负值回路。这就违反了先前的限制。下面将以此为依据考虑计算从源点v0到其他顶点u的最短路径的长度dist[u]。

贝尔曼-福特算法实现过程

算法思路

1. 在贝尔曼-福特算法中，构造一个最短路径长度的数组序列：dist¹ []，dist² []，…，dist^n-1 []。其中，dist¹ [u]表示从源点v0直接到终点u的最短路径的长度，即dist¹ [u]=ars[v0][u]；而 dist² [u]表示从源点v0出发最多经过两条弧（一个中间顶点）到达终点u的最短路径的长度……dist^k [u]是从源点v0出发最多经过不构成带负长度回路的k条弧（k-1个中间顶点）到达终点u的最短路径的长度。算法的结果就是计算出dist^n-1 [u]。
2. 可以用递推方式计算dist^n-1 []。设已经求出dist^k-1 [i]，i=0,1,2,…,n-1。此即从源点v0出发最多经过不构成带负长度回路的k-1条到达终点i的最短路径的长度。从图的邻接矩阵中可以找到从任一顶点i直接到达另一顶点u的距离Arc[j][u]，计算min{dist^k-1[i]+arcs[i][u]}，用它与dist^k-1[u]比较，取小者作为dist^k[u]的值，就可得到从源点v0出发最多经过k条弧（k-1个中间顶点）构成不带负长度回路而到达终点u的最短路径的长度。因此，可得递推公式：
   dist¹[u]=arcs[v0][u];
   dist^k[u]=min{dist^k-1[u]，dist^k-1[i]+arcs[i][u]}
3. 下面给出计算带权有向图的最短路径长度的贝尔曼-福特算法。算法中为了迭代地求dist^k[].使用了一个辅助数组distTemp[]来存放一次选代过程中dist[]的中间结果。一次迭代开始时先把dist[]复制到distTemp[]，迭代过程中把中间结果记录在distTemp[]中（中间结果不能放在dist[]中），一次迭代结束后再把distTemp[]复制回 dist[].算法结束时dist[]中存放的值等于dist^n-1[]。
   

代码实现

#include "AdjListDirNetwork.h"
///过程函数
template<class ElemType,class WeightType> void
ShortestPathBelLnamFord(const AdjListDirNetwork<ElemType,WeightType> &g,int v0,int *path,WeightType *dist)
{
   
    WeightType *distTemp,minVal,infinity=g.GetInfinity();
    int v,u,vexNum