计算机体系结构 第3章 流水线技术（2）

第3章 流水线技术

3.3 非线性流水线的调度

• 在非线性流水线中，存在反馈回路，当一个任务在流水线中流过时，可能要多次经过某些段。

• 流水线调度要解决的问题：

  • 应按什么样的时间间隔向流水线输入新任务，才能既不发生功能段使用冲突，又能使流水线有较高的吞吐率和效率？

3.3.1 单功能非线性流水线的最优调度

预约表

• 横向（向右）：时间（一般用时钟周期表示）
• 纵向（向下）：流水线的段

本教材的例子：一个5功能段非线性流水线预约表 P65

预约表相关说明

• 如果在第n个时钟周期使用第k段，则在第k行和第n列的交叉处的格子里有一个√（任意符号）。
• 如果在第k行和第n列的交叉处的格子里有一个√，则表示在第n个时钟周期要使用第k段。

引入预约表的原因

• 线性流水线能够用流水线连接图唯一表示，非线性流水线则不能。
• 连接图不能唯一表示非线性流水线的工作流程，要引入流水线预约表

一个典型的非线性流水线的示例及其预约表如下：

⚠️：一张预约表可能与多个流水线连接图相对应，可能有多种反馈回路对应一张预约表

---

流水线的启动距离

• 向一条非线性流水线的输入端连续输入两个任务之间的时间间隔称为非线性流水线的启动距离。

禁用启动距离

• 会引起非线性流水线功能段使用冲突的启动距离则称为禁用启动距离

启动距离和禁用启动距离一般都用时钟周期数来表示，是一个正整数。

最优调度方法

1. 根据预约表写出禁止表F

• 禁止表F：一个由禁用启动距离构成的集合。

• 具体方法

  • 对于预约表的每一行的任何一对√，用它们所在的列号相减（大的减小的），列出各种可能的差值，然后删除相同的，剩下的就是禁止表的元素。

  • 对于下图的启动表

• 第一行的差值只有一个：8；第二行的差值有3个：1，5，6；第3行只有一个√或x，没有差值；第4和第5行的差值都只有一个：1；

• 其禁止表是：F= { 1，5，6，8 }

2. 根据禁止表F写出初始冲突向量$C_0$

• 实质：进行从一个集合到一个二进制位串的变换

• 冲突向量C：一个N位的二进制位串。

• 设$C_0=（c_N{c}_{N-1}\dots c_i\dots c_2{c}_1）$，则：
  $${\mathbf{C}}_{\mathbf{i}}=\{\begin{array}{ll}1& \mathrm{i}\in \mathrm{F}\\ 0& \mathrm{i}\notin \mathrm{F}\end{array}$$

  • $c_i=0$ ：允许间隔i个时钟周期后送入后续任务

  • $c_i=1$ ：不允许间隔i个时钟周期后送入后续任务

• 对于上面的例子 F = { 1 ， 5 ， 6 ， 8 } F= \{ 1，5，6，8 \} F={1，5，6，8}，则$C_0=（10110001）$

3. 根据初始冲突向量$C_0$画出状态转换图

• 当第一个任务流入流水线后，初始冲突向量$C_0$决定了下一个任务需间隔多少个时钟周期才可以流入。

• 假设第二个任务是在与第一个任务间隔j个时钟周期流入，这时，由于第一个任务已经在流水线中前进了j个时钟周期，其相应的禁止表中各元素的值都应该减去j，并丢弃小于等于0的值。

• 对冲突向量来说，就是逻辑右移j位（左边补0）。

  • 实质是对冲突向量进行“或”运算。 （其中:$SH{R}^{(j)}$表示逻辑右移j位 ）

  $$SH{R}^{(j)}（C_0）\vee C_0$$

• 推广到更一般的情况

  • 假设: $C_k$：当前的冲突向量、$j$: 允许的时间间隔

  • 则新的冲突向量为：（⚠️所有计算都是与初始冲突向量$C_0$进行“或”操作）
    $$SH{R}^{(j)}（C_k）\vee C_0$$

  • 对于所有允许的时间间隔都按上述步骤求出其新的冲突向量，并且把新的冲突向量作为当前冲突向量，反复使用上述步骤，直到不再产生新的冲突向量为止。

• 从初始冲突向量$C_0$出发，针对初始冲突向量每个0，反复应用上述步骤，可以求得所有的冲突向量以及产生这些向量所对应的时间间隔。由此可以画出用冲突向量表示的流水线状态转移图。

  • 有向弧：表示状态转移的方向
  • 弧上的数字：表示引入后续任务（从而产生新的冲突向量）所用的时间间隔（时钟周期数）

示例：对于禁止表 F = { 1 ， 5 ， 6 ， 8 } F= \{ 1，5，6，8 \} F={1，5，6，8} 对应的初始向量$C_0=（10110001）$

（1） 引入后续任务可用的时间间隔为：2、3、4、7个时钟周期

• 如果采用2，则新的冲突向量为：$（00101100）\vee （10110001）=（10111101）$
• 如果采用3，则新的冲突向量为：$（00010110）\vee （10110001）=（10110111）$
• 如果采用4，则新的冲突向量为：$（00001011）\vee （10110001）=（10111011）$
• 如果采用7，则新的冲突向量为：$（00000001）\vee （10110001）=（10110001）$

（2）对于新向量（10111101），其可用的时间间隔为2个和7个时钟周期。用类似上面的方法，可以求出其后续的冲突向量分别为$（10111101）$和$（10110001）$。
（3）对于其他新向量，也照此处理。
（4）在此基础上，画出状态转移示意图。

4. 根据状态转换图写出最优调度方案

• 根据流水线状态图，由初始状态出发，任何一个闭合回路即为一种调度方案。
• 列出所有可能的调度方案，计算出每种方案的平均时间间隔，从中找出其最小者即为最优调度方案。
• 上例中，各种调度方案及其平均间隔时间。
  • 最佳方案：（3，4）：平均间隔时间：3.5个时钟周期（吞吐率最高） （ $\frac{3+4}{2}=3.5$ ）
  • 方案（4，3）的平均间隔时间也是3.5 ，但它不是最佳方案，原因是：当任务数是奇数时，方案(4,3)中最后一个任务是间隔4个时钟周期，而方案(3,4)中最后一个任务是间隔3个时钟周期。所以，只有方案(3,4)是最优的。
  • 方案（3，4）是一种不等时间间隔的调度方案，与等间隔的调度方案相比，在控制上要复杂得多。为了简化控制，也可以采用等间隔时间的调度方案，但吞吐率和效率往往会下降不少。

3.3.2 多功能非线性流水线的调度

以双功能（功能A和B）非线性流水线为例。

1. 状态转移图中结点状态的表示

   • 由两个冲突向量构成的冲突矩阵，这两个冲突向量分别对应于下一个任务的功能是A类和B类的情况。

2. 初始结点有两个，分别对应于第一个任务是A类和B类的情况。

   • 当第一个任务是A类时，冲突矩阵为$M_A^{(0)}$。
     当第一个任务是B类时，冲突矩阵为$M_B^{(0)}$。

   $$M_A^{(0)}=\left[\begin{array}{l}{C}_{AA}\\ C_{AB}\end{array}\right]M_B^{(0)}=\left[\begin{array}{l}{C}_{BA}\\ C_{BB}\end{array}\right]$$

   其中：

   • C p q （ p , q ∈ { A , B } ） C_{pq}（p,q∈\{A, B\}） Cpq​（p,q∈{A,B}）表示的是：在一个$p$类任务流入流水线后，对后续$q$类任务的冲突向量。它们可以由预约表求得。
   • $C_{pq}$共有$2^2=4$个。
   • 对于$N$功能流水线，这种冲突向量有$N^2$个。

3. 由下式求得后续状态的冲突矩阵
   $$SH{R}^{(j)}（M_k）\vee M_r^{(0)}$$
   其中：

   • $M_k$：当前状态
   • $r$：下一个流入任务的类型（A或B）
   • $i$：当前状态允许的流入$r$型任务的时间间隔
   • $SH{R}^{(j)}（M_k）$：把当前状态中的各冲突向量逻辑右移$j$位
   • 例如：$SH{R}^{(3)}（M_k）\vee M_A^{(0)}$表示的是：把当前状态$M_k$中的各冲突向量逻辑右移3位，再与初始矩阵$M_A^0$进行“或”运算。

示例：有一条3段双功能非线性流水线，实现的功能是A和B，其预约表分别如表1和表2所示。各段的通过时间都是一个时钟周期。请找出该流水线单独处理A类任务和单独处理B类任务以及混合处理两类任务的最优调度方案。

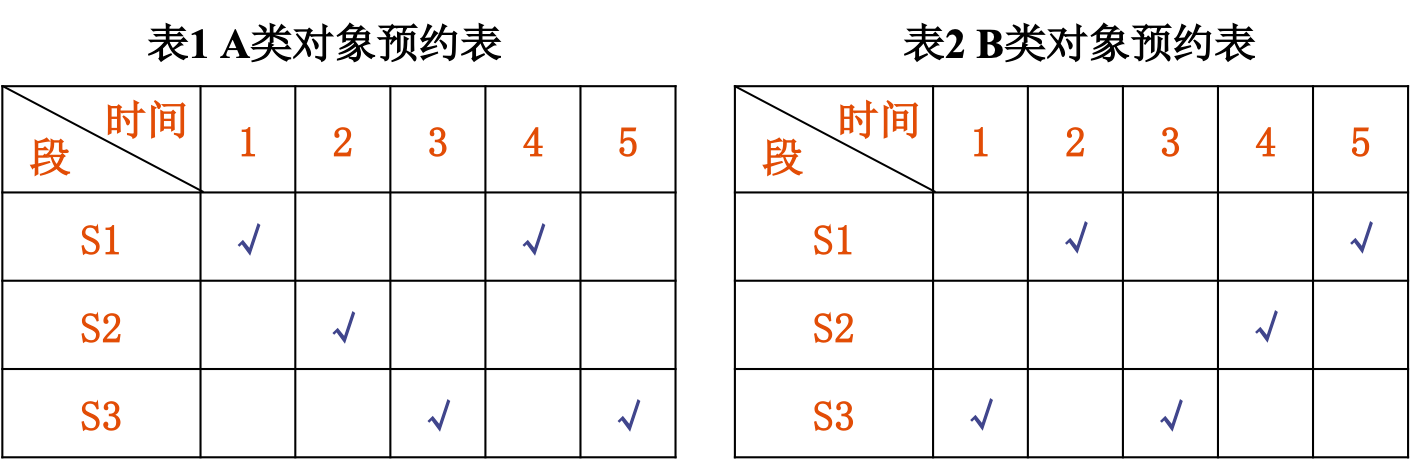
解：

（1） 把两个预约表重叠起来，得到如表3所示的预约表。

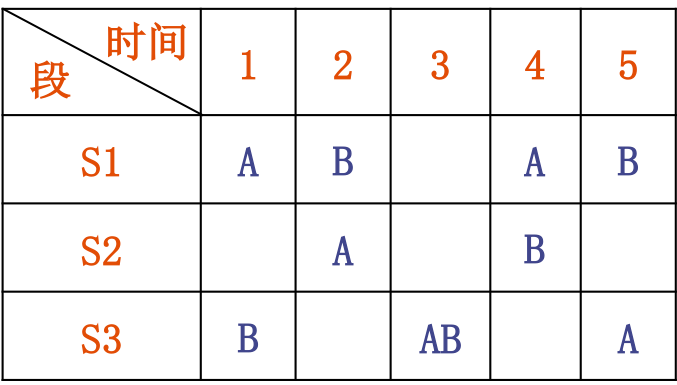
（2）由预约表求初始冲突向量和初始冲突矩阵
$$M_A^{(0)}=\left[\begin{array}{l}{C}_{AA}\\ C_{AB}\end{array}\right]M_B^{(0)}=\left[\begin{array}{l}{C}_{BA}\\ C_{BB}\end{array}\right]$$

• $C_{AA}$：一个A类任务流入流水线后，对下一个A类任务进入流水线的时间间隔的限制。
  • 根据预约表表1可知，禁用时间间隔是2和3，故禁止表为： { 2 ， 3 } \{2，3\} {2，3}，所以$C_{AA}=（0110）$。
• $C_{BB}$：一个B类任务流入流水线后，对下一个B类任务进入流水线的时间间隔的限制。
  • 根据预约表表2可知，禁用时间间隔是2和3，所以$C_{BB}=（0110）$。
• $C_{AB}$：一个A类任务流入流水线后，对下一个B类任务进入流水线的时间间隔的限制。根据预约表表3可知：
  • 为了避免在S1发生冲突，禁用时间间隔是：$4-2=2$
  • 在S2，不会发生冲突，这是因为根据表3，A类任务先于B类任务通过S2，而现在的实际情况又是A类任务先于B类任务流入流水线；
  • 为了避免在S3发生冲突，禁用时间间隔是：$3-1=2，5-1=4，5-3=2$
  • 综合起来，有：$C_{AB}=（1010）$
• $C_{BA}$ ：表示一个B类任务流入流水线后，对下一个A类任务进入流水线的时间间隔的限制。根据预约表表3可知：
  • 为了避免在S1发生冲突，禁用时间间隔有： $2-1=1，5-1=4，5-4=1$
  • 为了避免在S2发生冲突，禁用时间间隔是：$4-2=2$
  • 在S3，不会发生冲突，这是因为根据表3，B类任务先于A类任务通过S3，或者同时通过S3（第3个时钟周期），而现在的实际情况又是B类任务先于A类任务流入流水线。
  • 综合起来，有：$C_{BA}=（1011）$

（3）由初始冲突矩阵画出状态图

• 如果第一个流入的任务是A类，初始状态就是$M_A^{(0)}$ ；如果第一个流入的任务是B类，则初始状态是$M_B^{(0)}$ 。
• 求所有后续状态的冲突矩阵：
  • 例如：在流入一个A类任务后，从$C_{AA}=（0110）$可知，可以隔1个或4个时钟周期再流入一个A类任务。
    • 假设是前者，则把初始状态$M_A^{(0)}$ 中的各冲突向量同时右移一位（即进行$SH{R}^{(1)}$操作），再与$M_A^{(0)}$ 进行或运算，可以得到新的冲突矩阵。
    • 根据该矩阵的第一个冲突向量$（0111）$可知，只有隔4个时钟周期流入一个A类任务，才能不发生冲突。把冲突矩阵中的各冲突向量同时右移4位（即进行$SH{R}^{(4)}$操作），再与$M_A^{(0)}$ 进行按位或运算，可以得到新的冲突矩阵。
  • 再如，在流入一个A类任务后，从$C_{AB}=（1010）$可知，可以隔1个或3个时钟周期再流入一个B类任务。
    • 假设是前者，则把初始状态$M_A^{(0)}$ 中的各冲突向量同时右移一位（即进行$SH{R}^{(1)}$操作），再与$M_B^{(0)}$ 进行或运算，可以得到新的冲突矩阵。
    • 据此可知，允许的流入为：或者是隔3个时钟周期流入一个A类任务，或者是隔4个时钟周期流入一个B类任务。按类似与上述类似的方法，又可以得到新的冲突矩阵。
• 求出所有可能的状态后，就可以画出状态图。
  • 弧线上的标记“$r.i$”表示：隔$i$个时钟周期流入$r$类的任务。

最后，可以求得状态转换图如下

（4）由状态图得出最优调度方案

• 从状态图可以找出各种情况下的最优调度方案：
  • 只流入A类任务的最优调度方案是：（A.1，A.4）
  • 流入B类任务的最优调度方案是：（B.1，B.4）
  • 混合流入A、B两类任务的最优调度方案是：（B.1？，A.3？，A.4）（个人觉得不一定，与任务流入的顺序有关系）

3.3.3 非线性流水线的优化调度方法

L.E.Shar于1972年提出了流水线最小平均启动距离的限制范围

1. 下限是预约表中任意一行里“×”或“√”的最多个数
2. 小于或等于状态图中任意一个简单循环的平均启动距离；
3. 最小平均启动距离的上限是冲突向量中1的个数再加上1

1992年，L.E.Shar证明了上述限制范围

最有用的是第1条。预约表中×”或“√”最多的行一定是瓶颈流水段

举例：一个不是最优的流水线

上一条4功能段的非线性流水线，每个功能段的延迟时间都相等，已知它的预约表，求：

1. 写出流水线的禁止向量和初始冲突向量。
2. 画出调度流水线的状态图。
3. 求最小启动循环和最小平均启动距离。
4. 求平均启动距离最小的恒定循环。

解答：

（1）禁止向量为：$F=(2，4，6)$、初始冲突向量：$C_0=101010$

（2）构造状态图

• S逻辑右移2、4、6位时，移出1，不作任何处理

• 逻辑右移1、3、5时：

  • $C_0$右移1位之后：$010101\vee 101010＝111111$（计作$C_1$）
  • $C_0$右移3位之后：$000101\vee 101010＝101111$（计作$C_2$）
  • $C_0$右移5位之后：$000001\vee 101010＝101011$（计作$C_3$）
  • $C_0$右移7位或大于7位后：还原到它本身$101010$。

• $C_2=101111$ 右移5位之后：$000001\vee 101010＝101011$（$C_3$）

• $C_3=101011$右移3位之后：$000101\vee 101010＝101111$（$C_2$）

• $C_3=101011$右移5位之后：$000001\vee 101010＝101011$（$C_3$）

构造出状态图如下：

（3）简单循环：状态图中各种冲突向量只经过一次的启动循环。所有的简单循环如下：

简单循环	平均启动距离
（1，7）	4
（3，7）	5
（5，7）	6
（3，5，7）	5
（5，3，7）	5
（3，5）	4
（5）	5
（7）	7

根据上述，不是最优的流水线

(4)根据上述原理，采用预留算法来调度非线性流水线，可以实现最优，具体步骤如下：

• 第1步：确定最小平均启动距离，为预约表中任意一行中“×”的最多个数。
• 第2步：确定最小启动循环，以恒定循环作为最小启动循环。
• 第3步：采用预留算法，插入非计算延迟段实现最小启动循环

例如：

• 对于上个例子的预约表，在同一行中“×”最多的为2个，因此，最小平均距离可以达到2。

• 最小启动循环可以是(2)、(1,3)、(1,1,4)、(1,2,3)、……。现取恒定循环(2)。

• 每一行中与第1个“×”的距离为2的倍数的位置都要预留出来。

  • S3行的第2个“×”从周期5延迟到周期6
  • S2行的第2个“×”从周期6延迟到周期7
  • S1行的第2个“×”从周期7延迟到周期8
  • 实际上，只需要在流水段S4的输出端到流水段S3的输入端中间插入一个非计算延迟D1。

可以得出采用预留调度算法的预约表如下图：

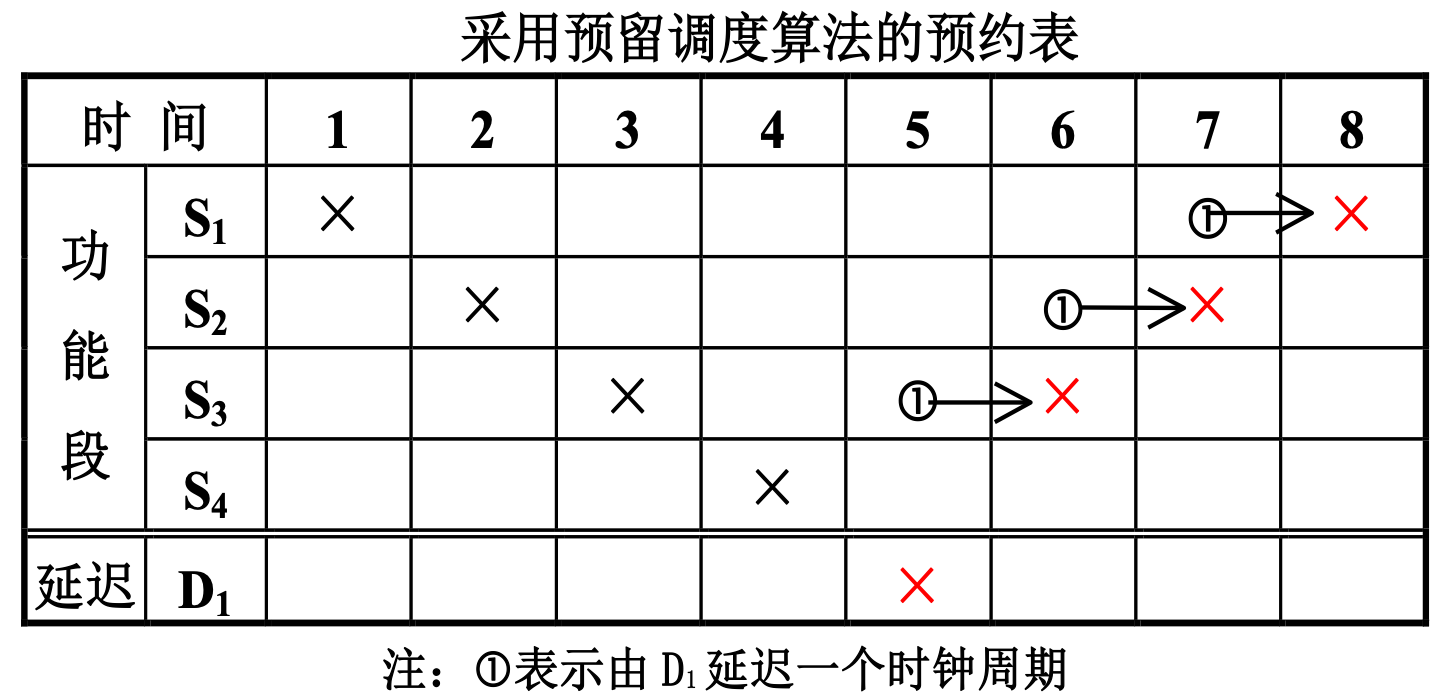
增加了一个非计算延迟流水段 D1 的流水线连接图：

重复步骤（1）（2）可以得出其流水线状态图如下：