Round13—图基本概念及图的遍历

判断题：

1-1无向连通图至少有一个顶点的度为1。（F） (1分)

解析：无向图连通只要保证每对接点都可达即可，因此我们考虑，两个节点的图，两个节点之间有2个重边，因此题设是不成立的。

1-2用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关。（F） (1分)

解析：使用邻接表占用空间与这个图是有向图还是无向图有关。

如果是无向图，那么空间就是n+2e，如果是有向图就是n+e。（n为节点数，e为边数）。

1-3用邻接矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关（T）。 (1分)

解析：邻接矩阵G[x][y]表示x->y这条边的权重，因此n各节点需要两两组合，空间大小为n^2。

1-4在一个有向图中，所有顶点的入度与出度之和等于所有边之和的2倍。（T） (1分)

解析：离散数学图论当中的定理。

1-5在任一有向图中，所有顶点的入度之和等于所有顶点的出度之和。（T） (1分)

解析：离散数学当中的定理。

1-6如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G中一定有回路。（F） (2分)

解析：因为不论是bfs还是dfs我们在遍历的时候都进行了标记也就是当一个节点被标记了的时候这个节点就不会重复访问。

因此两次bfs才访问完所有的节点不是因为有回路而是因为这个图有两个连通分量。

1-7如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则G一定有2个连通分量。（T） (2分)

解析：综上分析。

1-8无向连通图所有顶点的度之和为偶数。（T） (1分)

解析：根据离散数学的定理，我们知道度=边数*2，因而度一定是个偶数。

1-9无向连通图边数一定大于顶点个数减1。（F） (1分)

解析：一个无向图是连通的我们考虑最极限的情况就是他是一棵n各节点的树，因而度应该是大于等于n-1的。

单选题：

2-1若无向图G =（V，E）中含10个顶点，要保证图G在任何情况下都是连通的，则需要的边数最少是： (3分)

• 45
• 37
• 36
• 9

解析：我们考虑鸽巢原理，我们只需要其中的9个顶点形成一个完全连通图，也就是每个点与其点都有一条边直连，再将剩下的一个顶点与这个完全连通图形成连通图即可，因此9*8/2+1=37。

2-2给定一个有向图的邻接表如下图，则该图有__个强连通分量。(3分)

• 4 {{0, 1, 5}, {2}, {3}, {4}}
• 3 {{2}, {4}, {0, 1, 3, 5}}
• 1 {0, 1, 2, 3, 4, 5}
• 1 {0, 5, 1, 3}

解析：有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

通过邻接表画图我们可以得到所有的强连通分量。

2-3给定有向图的邻接矩阵如下：

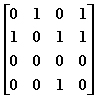
顶点2（编号从0开始）的出度和入度分别是：

• 3, 1
• 1, 3
• 0, 2
• 2, 0

解析：第三行做和为出度，第三列做和为入度。

2-4

下面给出的有向图中，有__个强连通分量。(2分)

• 1 ({0,1,2,3,4})
• 1 ({1,2,3,4})
• 2 ({1,2,3,4}, {0})
• 5 ({0}, {1}, {2}, {3}, {4})

解析：根据强连通分量的定义，我们可以看出{1,2,3,4}，是一个极大连通子图。

2-5下面给出的有向图中，各个顶点的入度和出度分别是：(1分)

• 入度: 0, 2, 3, 1, 2; 出度: 3, 2, 1, 1, 1
• 入度: 3, 2, 1, 1, 1; 出度: 0, 2, 3, 1, 2
• 入度: 3, 4, 4, 2, 3; 出度: 3, 4, 4, 2, 3
• 入度: 0, 1, 2, 1, 1; 出度: 3, 2, 1, 1, 1

解析：不难计算。

2-6如果G是一个有36条边的非连通无向图，那么该图顶点个数最少为多少？(3分)

• 7
• 8
• 9
• 10

解析：这个题不应该考虑自环与重边。

首先是非连通的，我们考虑极限情况就是有两个连通分量，其中一个连通分量只有一个节点。

另外一个连通分量形成完全连通图。

2-7下面关于图的存储的叙述中，哪一个是正确的？ (1分)

• 用相邻矩阵法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关
• 用相邻矩阵法存储图，占用的存储空间数只与图中边数有关，而与结点个数无关
• 用邻接表法存储图，占用的存储空间数只与图中结点个数有关，而与边数无关
• 用邻接表法存储图，占用的存储空间数只与图中边数有关，而与结点个数无关

解析：根据上面的题目我们不难选择。

2-8关于图的邻接矩阵，下列哪个结论是正确的？ (1分)

• 有向图的邻接矩阵总是不对称的
• 有向图的邻接矩阵可以是对称的，也可以是不对称的
• 无向图的邻接矩阵总是不对称的
• 无向图的邻接矩阵可以是不对称的，也可以是对称的

解析：显然。

2-9设N个顶点E条边的图用邻接表存储，则求每个顶点入度的时间复杂度为： (2分)

• O(N)
• O(N​2​​)
• O(N+E)
• O(N×E)

解析：邻接表求入度需要遍历整个邻接表也就是n+e，而求出度是n。

2-10在一个无向图中，所有顶点的度数之和等于所有边数的多少倍？ (2分)

• 1/2
• 1
• 2
• 4

解析：离散数学定理。

2-11同上

2-12在任一有向图中，所有顶点的入度之和与所有顶点的出度之和的关系是： (1分)

• 相等
• 大于等于
• 小于等于
• 不确定

解析：离散数学定理。

2-13设无向图的顶点个数为N，则该图最多有多少条边？ (1分)

• N−1
• N(N−1)/2
• N(N+1)/2
• N^2​​

解析：还是不考虑重边与自环，想成完全连通图即可。

2-14下列关于无向连通图特征的叙述中，正确的是： (2分)

1. 所有顶点的度之和为偶数
2. 边数大于顶点个数减1
3. 至少有一个顶点的度为1

• 只有1
• 只有2
• 1和2
• 1和3

解析：根据前面的题目我们可以选出。

2-15若无向图G =（V，E）中含7个顶点，要保证图G在任何情况下都是连通的，则需要的边数最少是： (3分)

• 6
• 15
• 16
• 21

解析：鸽巢原理。

2-16在N个顶点的无向图中，所有顶点的度之和不会超过顶点数的多少倍？ (2分)

• 1
• 2
• (N−1)/2
• N−1

解析：形成一棵树。

2-17对于一个具有N个顶点的无向图，要连通所有顶点至少需要多少条边？ (2分)

• N−1
• N
• N+1
• N/2

解析：同上

2-18具有N（N>0）个顶点的无向图至多有多少个连通分量？ (2分)

• 0
• 1
• N−1
• N

解析：无边

2-19一个有N个顶点的强连通图至少有多少条边？ (2分)

• N−1
• N
• N+1
• N(N−1)

解析：无向图有n-1个即可，有向图需要加一个形成环。

2-20如果G是一个有28条边的非连通无向图，那么该图顶点个数最少为多少？ (3分)

• 7
• 8
• 9
• 10

解析：鸽巢原理。

2-21对于有向图，其邻接矩阵表示比邻接表表示更易于： (2分)

• 求一个顶点的入度
• 求一个顶点的出边邻接点
• 进行图的深度优先遍历
• 进行图的广度优先遍历

解析：这是邻接矩阵的特性。

2-22对于一个具有N个顶点的无向图，若采用邻接矩阵表示，则该矩阵的大小是： (1分)

• N−1
• N
• (N−1)^​2​​
• N​^2​​

解析：不说了。

2-23若一个有向图用邻接矩阵表示，则第i个结点的入度就是： (1分)

• 第i行的元素个数
• 第i行的非零元素个数
• 第i列的非零元素个数
• 第i列的零元素个数

解析：不说了。

2-24下列选项中，不是下图深度优先搜索序列的是：(2分)

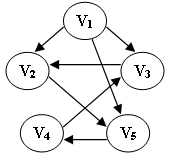
• V​1​​, V​5​​, V​4​​, V​3​​, V​2​​
• V​1​​, V​3​​, V​2​​, V​5​​, V​4​​
• V​1​​, V​2​​, V​5​​, V​4​​, V​3​​
• V​1​​, V​2​​, V​3​​, V​4​​, V​5​​

解析：根据bfs的特性我们可以选出第四个，bfs的顺序与存储顺序有关与标号大小无关。

2-25若某图的深度优先搜索序列是{V1, V4, V0, V3, V2}，则下列哪个图不可能对应该序列？ (2分)

• 
• 
• 
• 

解析：根据dfs的特性我们会知道第三个是不对的。

2-26若某图的深度优先搜索序列是{V2, V0, V4, V3, V1}，则下列哪个图不可能对应该序列？ (2分)

• 
• 
• 
• 

解析：答案第四个。

2-27已知无向图G含有16条边，其中度为4的顶点个数为3，度为3的顶点个数为4，其他顶点的度均小于3。图G所含的顶点个数至少是：(4分)

• 10
• 11
• 13
• 15

解析：16边度就是32，n*2+3*4+3*4=32，我们知道答案就是11.

2-28给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历，则得到的一种顶点序列为：(2分)

• V1,V5,V4,V7,V6,V2,V3
• V1,V2,V3,V4,V7,V6,V5
• V1,V5,V4,V7,V6,V3,V2
• V1,V5,V6,V4,V7,V2,V3

解析：看清楚是节点标号还是节点。

2-29图的广度优先遍历类似于二叉树的：(1分)

• 先序遍历
• 中序遍历
• 后序遍历
• 层次遍历

2-30给定无向图G，从V0出发进行深度优先遍历访问的边集合为： {(V0,V1), (V0,V4), (V1,V2), (V1,V3), (V4,V5), (V5,V6)}。则下面哪条边不可能出现在G中？ (3分)

• (V0,V2)
• (V0,V6)
• (V1,V5)
• (V4,V6)

解析：我们假设(V1,V5)存在会发现dfs顺序与题设不吻合。

2-31给定一有向图的邻接表如下。从顶点V1出发按深度优先搜索法进行遍历，则得到的一种顶点序列为： (2分)

• V1,V2,V3,V5,V4
• V1,V3,V4,V5,V2
• V1,V4,V3,V5,V2
• V1,V2,V4,V5,V3

解析：这里是标号。

2-32已知一个图的邻接矩阵如下，则从顶点V1出发按深度优先搜索法进行遍历，可能得到的一种顶点序列为： (2分)

• V1,V2,V3,V4,V5,V6
• V1,V2,V4,V5,V6,V3
• V1,V3,V5,V2,V4,V6
• V1,V3,V5,V6,V4,V2

解析：dfs的定义。

2-33如果从无向图的任一顶点出发进行一次深度优先搜索可访问所有顶点，则该图一定是： (2分)

• 连通图
• 完全图
• 有回路的图
• 一棵树

解析：显然。

2-34在图中自a点开始进行广度优先遍历算法可能得到的结果为： (2分)

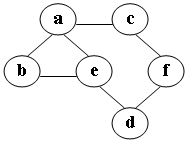
• a, e, d, f, c, b
• a, c, f, e, b, d
• a, e, b, c, f, d
• a, b, e, c, d, f

解析：广度优先遍历也就是bfs是按层遍历。

2-35在图中自c点开始进行广度优先遍历算法可能得到的结果为： (2分)

• c,a,b,e,f,d
• c,a,f,d,e,b
• c,f,a,d,e,b
• c,f,a,b,d,e

解析；同上。

2-36如果无向图G必须进行两次广度优先搜索才能访问其所有顶点，则下列说法中不正确的是： (2分)

• G肯定不是完全图
• G中一定有回路
• G一定不是连通图
• G有2个连通分量

解析：由于不论是bfs还是dfs我们在遍历的过程当中都是边遍历边标记，因此访问过的就不会重复访问，因此与图有没有环没有关系。

2-37给定一有向图的邻接表如下。若从v1开始利用此邻接表做广度优先搜索得到的顶点序列为：{v1, v3, v2, v4, v5}，则该邻接表中顺序填空的结果应为： (3分)

• v2, v3, v4
• v3, v2, v4
• v3, v4, v2
• v4, v3, v2

解析：从题能看出来这里是存储的结点，而不是结点的标号。

2-38给定一有向图的邻接表如下。从顶点V1出发按广度优先搜索法进行遍历，则得到的一种顶点序列为： (2分)

• V1,V2,V3,V4,V5
• V1,V2,V3,V5,V4
• V1,V3,V2,V4,V5
• V1,V4,V3,V5,V2

解析：这里是结点的标号，而不是结点。

2-39已知一个图的邻接矩阵如下，则从顶点V1出发按广度优先搜索法进行遍历，可能得到的一种顶点序列为： (2分)

• V1,V2,V3,V5,V4,V6
• V1,V2,V4,V5,V6,V3
• V1,V3,V5,V2,V4,V6
• V1,V3,V5,V6,V4,V2

解析：考察bfs的遍历方式。

2-40下列说法不正确的是： (2分)

• 图的遍历是从给定的源点出发每一个顶点仅被访问一次
• 遍历的基本算法有两种：深度遍历和广度遍历
• 图的深度遍历是一个递归过程
• 图的深度遍历不适用于有向图

解析：图的遍历是一种对于图的普遍使用方法，与图的类型，图的实际存储结构没有关系。

bfs也就是广度优先搜索是队列实现的，而bfs也就是深度优先搜索是递归实现的。

2-41图的深度优先遍历类似于二叉树的： (1分)

• 先序遍历
• 中序遍历
• 后序遍历
• 层次遍历

解析：首先排除层次遍历，层次遍历是显然的bfs。

深度遍历我们往往是先访问结点，然后再递归下一个结点，因此是先序遍历。

2-42在图中自a点开始进行深度优先遍历算法可能得到的结果为： (2分)

• a, b, e, c, d, f
• a, c, f, e, b, d
• a, e, b, c, f, d
• a, e, d, f, c, b

解析：dfs的递归实现。

函数题：

6-1 邻接矩阵存储图的深度优先遍历 (20 分)

试实现邻接矩阵存储图的深度优先遍历。

函数接口定义：

void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );

其中MGraph是邻接矩阵存储的图，定义如下：

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;  /* 顶点数 */
    int Ne;  /* 边数   */
    WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */

函数DFS应从第V个顶点出发递归地深度优先遍历图Graph，遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时，要求按序号递增的顺序。题目保证V是图中的合法顶点。

裁判测试程序样例：

#include <stdio.h>

typedef enum {false, true} bool;
#define MaxVertexNum 10  /* 最大顶点数设为10 */
#define INFINITY 65535   /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex;      /* 用顶点下标表示顶点,为整型 */
typedef int WeightType;  /* 边的权值设为整型 */

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;  /* 顶点数 */
    int Ne;  /* 边数   */
    WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
bool Visited[MaxVertexNum]; /* 顶点的访问标记 */

MGraph CreateGraph(); /* 创建图并且将Visited初始化为false；裁判实现，细节不表 */

void Visit( Vertex V )
{
    printf(" %d", V);
}

void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );


int main()
{
    MGraph G;
    Vertex V;

    G = CreateGraph();
    scanf("%d", &V);
    printf("DFS from %d:", V);
    DFS(G, V, Visit);

    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例：给定图如下

5

输出样例：

DFS from 5: 5 1 3 0 2 4 6

AC代码：

void DFS(MGraph Graph, Vertex V, void(* Visit)(Vertex))
{
    Visit(V);
    Visited[V] = true;
    for(int i = 0; i < Graph->Nv; i++)
    {
        if(Visited[i] || Graph->G[V][i] == INFINITY)
            continue;
        if(Graph->G[V][i] != INFINITY)
            DFS(Graph, i, Visit);
    }
}

6-2 邻接表存储图的广度优先遍历 (20 分)

试实现邻接表存储图的广度优先遍历。

函数接口定义：

void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );

其中LGraph是邻接表存储的图，定义如下：

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;        /* 邻接点下标 */
    PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};

/* 顶点表头结点的定义 */
typedef struct Vnode{
    PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum];     /* AdjList是邻接表类型 */

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;     /* 顶点数 */
    int Ne;     /* 边数   */
    AdjList G;  /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */

函数BFS应从第S个顶点出发对邻接表存储的图Graph进行广度优先搜索，遍历时用裁判定义的函数Visit访问每个顶点。当访问邻接点时，要求按邻接表顺序访问。题目保证S是图中的合法顶点。

裁判测试程序样例：

#include <stdio.h>

typedef enum {false, true} bool;
#define MaxVertexNum 10   /* 最大顶点数设为10 */
typedef int Vertex;       /* 用顶点下标表示顶点,为整型 */

/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode; 
struct AdjVNode{
    Vertex AdjV;        /* 邻接点下标 */
    PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};

/* 顶点表头结点的定义 */
typedef struct Vnode{
    PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum];     /* AdjList是邻接表类型 */

/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{  
    int Nv;     /* 顶点数 */
    int Ne;     /* 边数   */
    AdjList G;  /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */

bool Visited[MaxVertexNum]; /* 顶点的访问标记 */

LGraph CreateGraph(); /* 创建图并且将Visited初始化为false；裁判实现，细节不表 */

void Visit( Vertex V )
{
    printf(" %d", V);
}

void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );

int main()
{
    LGraph G;
    Vertex S;

    G = CreateGraph();
    scanf("%d", &S);
    printf("BFS from %d:", S);
    BFS(G, S, Visit);

    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例：给定图如下

2

输出样例：

BFS from 2: 2 0 3 5 4 1 6

AC代码：

void BFS(LGraph Graph, Vertex S, void (* Visit)(Vertex))
{
    int *que = (int *)malloc((Graph->Nv + 100) * sizeof(int));
    int front = 0, rear = 0;

    que[rear++] = S;
    Visited[S] = true;
    while(front != rear)
    {
        int temp = que[front++];

        Visit(temp);

        PtrToAdjVNode to = Graph->G[temp].FirstEdge;
        while(to != NULL)
        {
            if(Visited[to->AdjV])
            {
                to = to->Next;
                continue;
            }

            que[rear++] = to->AdjV;
            Visited[to->AdjV] = true;
            to = to->Next;
        }
    }
}

注：这两个函数题涉及到回调函数。