本文详细介绍了广度优先搜索(BFS)和深度优先搜索(DFS)两种图搜索算法的基本概念、执行步骤及其应用案例。通过图解的方式展示了这两种算法的具体执行过程，并提供了多个编程示例帮助理解。
一、广度优先搜索(BFS)
1.简介
BFS，其英文全称是Breadth First Search。BFS并不使用经验法则算法。从算法的观点，所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。一般的实验里，其邻居节点尚未被检验过的节点会被放置在一个被称为open的容器中（例如队列或是链表），而被检验过的节点则被放置在被称为closed的容器中。（open-closed表)
广度优先搜索是一种对图进行搜索的算法。假设我们一开始位于某个顶点(即起点)，此 时并不知道图的整体结构，而我们的目的是从起点开始顺着边搜索，直到到达指定顶点(即终 点)。在此过程中每走到一个顶点，就会判断一次它是否为终点。广度优先搜索会优先从离起点 近的顶点开始搜索。
在执行广度优先搜索的过程中将构造出一棵广度优先树。一开始，该树仅含有根结点，就是源结点s。在扫描已发现结点u的邻接链表时，每当发现一个白色结点v，就将结点v和边(u，v)同时加入该棵树中。在广度优先树中，称结点u是结点v的前驱或者父结点。由于每个结点最多被发现一次，它最多只有一个父结点。广度优先树中的祖先和后代关系皆以相对于根结点s的位置来进行定义：如果结点u是从根结点s 到结点v的简单路径上的一个结点，则结点u是结点v的祖先，结点v是结点u的后代。
2.步骤
广度优先搜索类似于树的按层次遍历的过程。
假设从图中某顶点v出发，在访问了 v 之后依次访问 v 的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问，直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作为起始点，重复上述过程，直至图中所有顶点都被访问到为止。换句话说，广度优先搜索的过程是以v为起始点，由近至远，依次访问和 v 有路径相通且路径长度为1、2、…的顶点。
待访问的邻接点使用的数据结构队列。
- 将初始点（一个或多个）加入一个集合尾
- 从集合头取出点，判断初始点的周边点，将符合条件的点加入队列
- 重复 2 操作，直至集合为空。 ( 一般 每个点只加入队列一 次 )
适用情况：
- 一般在树或者图中，用BFS的可能性比较大。（最短路径）
3.图解
绿色节点是待搜索点，深灰色是未访问点，浅灰色是已经访问的点。
先将起始点加入到队列中。取队列首进行搜索（节点s）。
需要设置一个节点是否访问过的标记。
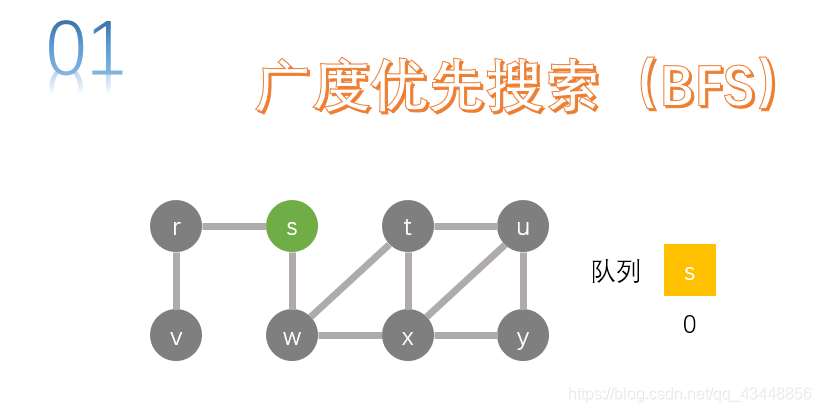
搜索s的邻接点，r、w是s的邻接点，将r、w加入队列中。
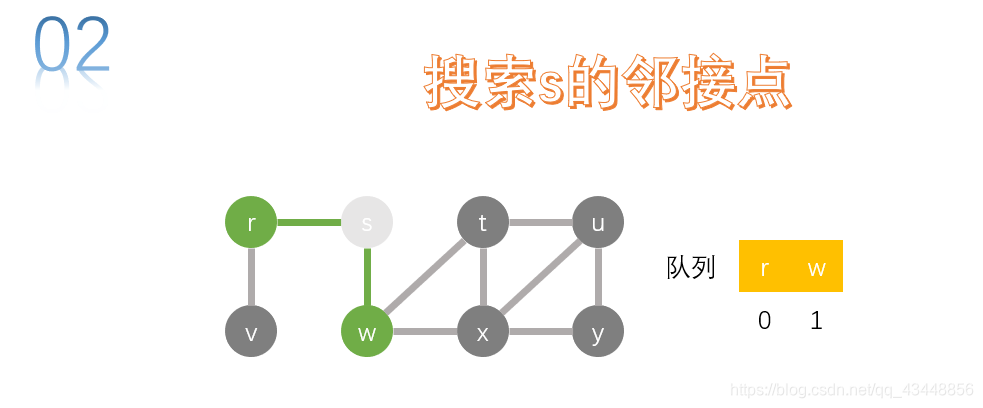
取队首节点r，进行搜索。v是r的邻接点，将v加入队列中。
取队首节点w，进行搜索。t、x是w的邻接点，将t、x加入队列中。
取队首节点v，进行搜索。v无邻接点。
取队首节点t，进行搜索。u、x是t的邻接点，x已经访问了，所以将u加入队列中。
取队首节点x，进行搜索。w、t、u、y是x的邻接点，w、t、u已经访问，所以将y加入队列。
取队首节点u，进行搜索。t、x、y是u的邻接点，t、x、y已经访问，无节点需要加入队列。
取队首节点y，进行搜索。u、x是y的邻接点，u、x已经访问，无需加入队列。
队列为空，结束广度优先搜索(BFS)。
访问的顺序：s、r、w、v、t、x、u、y
每个节点至多进入一次队列。广度优先搜索的特征为从起点开始，由近及远进行广泛的搜索。因此，目标顶点离起点越近，搜索结束得越快。
例题
第一题
题目链接
模板题
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> printFromTopToBottom(TreeNode* root) {
vector<int> num;
if(!root)
return num;
queue<TreeNode*> p;
p.push(root);
while(!p.empty()){
TreeNode* s = p.front();
p.pop();
num.push_back(s->val);
if(s->left)
p.push(s->left);
if(s->right)
p.push(s->right);
}
return num;
}
};
第二题
题目链接
将所有为1的点都加入队列之中进行bfs。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
int n,m;
int A[1010][1010],B[1010][1010];//如题意
queue<pair<int,int> >q;//队列
int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};//上下左右四个方向的坐标变换
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ ){
int a;
scanf("%1d", &a);
B[i][j] = -1;
if(a == 1){//将1的点都加入队列，并将B置为0
B[i][j] = 0;
q.push({i,j});
}
}
int cnt = 0;//记录是第几层
while(q.size()){//队列不空
int f = q.size();//获取该层的个数
cnt++;
for (int i = 0; i < f; i ++ ){//依次将该层的点出队列
pair<int, int> next = q.front();//获取到队首的值
q.pop();//将队首出队列
int x = next.first, y = next.second;
for (int j = 0; j < 4; j ++ ){//遍历四个方向
if (x+dx[j]>=0 && x+dx[j]<n && y+dy[j]>=0 && y+dy[j]<m && B[x+dx[j]][y+dy[j]]==-1){//坐标在地图内,而且这个点没有被拓展过
B[x+dx[j]][y+dy[j]] = cnt;
q.push({x+dx[j], y+dy[j]});//将满足的情况加入队列
}
}
}
}
for (int i = 0; i < n; i ++ ){
for (int j = 0; j < m; j ++ )
printf("%d ",B[i][j]);
printf("\n");
}
return 0;
}
第三题
#include <iostream>
#include <cstring>
#include <algorithm>
#include <deque>
using namespace std;
int n,m;
char str[510][510];
int d[510][510];//记录从起始点到该点的最小值
int bfs(){
memset(d,0x3f,sizeof(d));
deque<pair<int, int>> dp;
dp.push_back({0,0});//将起始点加入队列尾
d[0][0] = 0;
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1};//四个方向的位移
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1};//获取该格的线路（每个格子都是以左上角为标记）
char s[] = "\\/\\/";//四个不同方向的，对角线
while(dp.size()){
pair<int, int> f = dp.front();//去队列首
dp.pop_front();//去除队列首
int x = f.first, y = f.second;
for (int i = 0; i < 4; i ++ ){//遍历四个方向
int xx = x + dx[i], yy = y + dy[i];
if(xx >= 0 && xx<=n && yy>=0 && yy<=m){//验证方向合法
int w = 0;
if(s[i] != str[x+ix[i]][y+iy[i]])//方向上没有路径，需要改变路径方向
w = 1;
if(d[xx][yy] > d[x][y]+w){//若到达该点的值大于当前方案的值，则更换最小值
d[xx][yy] = d[x][y]+w;
if(w)//若需要改变方向，则将其加入到队列尾
dp.push_back({xx,yy});
else//若不需要改变方向，则将其加入到队列首
dp.push_front({xx,yy});
}
}
}
}
if(d[n][m] == 0x3f3f3f3f)//验证是否为初始值
return 0;
return 1;
}
int main()
{
int t;
scanf("%d",&t);
while (t -- ){
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ){
scanf("%s", str[i]);
}
if(bfs())
printf("%d\n",d[n][m]);
else
printf("NO SOLUTION\n");
}
return 0;
}
第四题
题目链接
模板题
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
pair<int, int> start,endd;
int n,m;
char str[160][160];
int d[160][160];
int bfs(){
queue<pair<int, int>> q;
q.push(start);
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
while(q.size()){
auto a = q.front();
q.pop();
for (int i = 0; i < 8; i ++ ){
int x = a.first + dx[i], y = a.second + dy[i];
if(x<0 || x>=n || y<0 || y>=m || str[x][y] == '*' || d[x][y] != 0)
continue;
d[x][y] = d[a.first][a.second] + 1;
if(x == endd.first && y == endd.second)
return d[x][y];
q.push({x,y});
}
}
return -1;
}
int main()
{
scanf("%d%d", &m, &n);
for (int i = 0; i < n; i ++ ){
getchar();
for (int j = 0; j < m; j ++ ){
scanf("%c", &str[i][j]);
if(str[i][j] == 'K')
start = {i,j};
else if(str[i][j] == 'H')
endd = {i,j};
}
}
printf("%d",bfs());
return 0;
}
二、深度度优先搜索(DFS)
1.简介
一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。最坏的情况算法时间复杂度为O(!n)。
2.步骤
假设初始状态是图中所有顶点未曾被访问，则深度优先搜索可从图中某个顶点v出发，访问此顶点，然后依次从v得未被访问得邻接点出发深度优先搜索图，直至图中所有和v由路径相通的顶点都被访问到；若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
从图中某顶点v出发：
- 访问顶点v；
- 依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问；
- 若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。
3.图解
绿色为当前所在节点，深灰色为未访问的节点，浅灰色为已经访问过的节点。
设置起始点为节点s，进行深度优先搜索。一般记录DFS的路径使用栈或者递归进行。
需要设置一个节点是否访问过的标记。
r和w是s的邻接点，我们先搜索节点r。对r进行深度优先搜索。
r的邻接点只要节点v，所有我们搜索v。对v进行深度优先搜索。
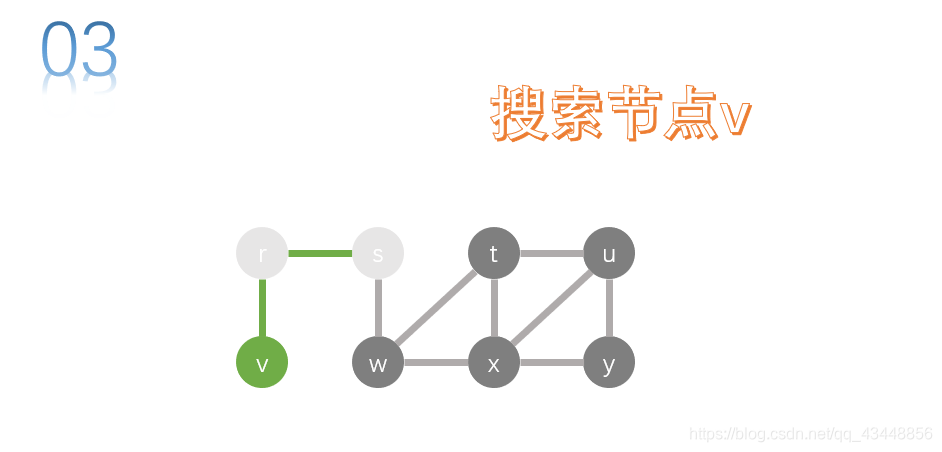
v没有邻接点，也就意味着到底了，应该返回上一级节点，也就是返回r，搜索r的其它邻接点。
r只要v一个邻接点，已经被访问了，所有r没有未访问的邻接点了，所以应该返回r的上一级，也就是返回s，搜索s的未访问的邻接点。
s的邻接点有r、w，w没有被访问，所以我们下一步搜索w。对w进行深度优先搜索。
w的邻接点有t、x，两个节点都没有被访问，我们先访问t。对t进行深度优先搜索。
t的邻接点有u、x、w，w已经被访问了，所以就剩下u和x，我们先对u进行搜索。
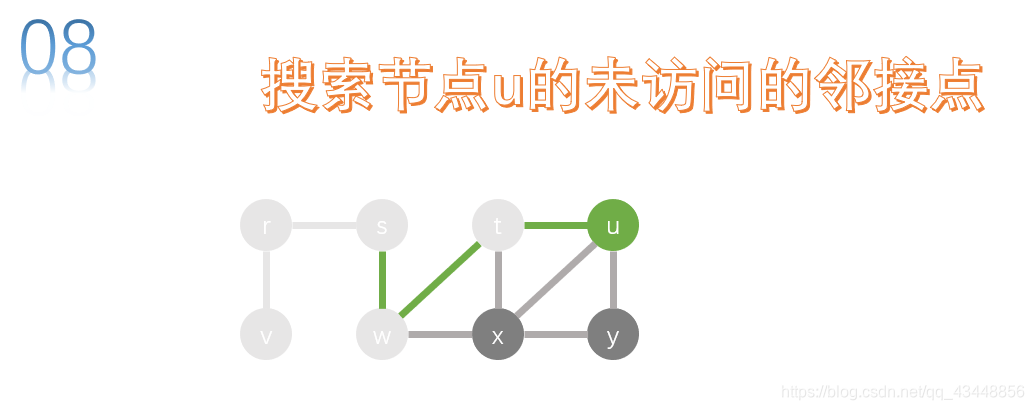
u的邻接点有y、x、t，t已经被访问了，所以就剩下x、y，我们先对y进行搜索。
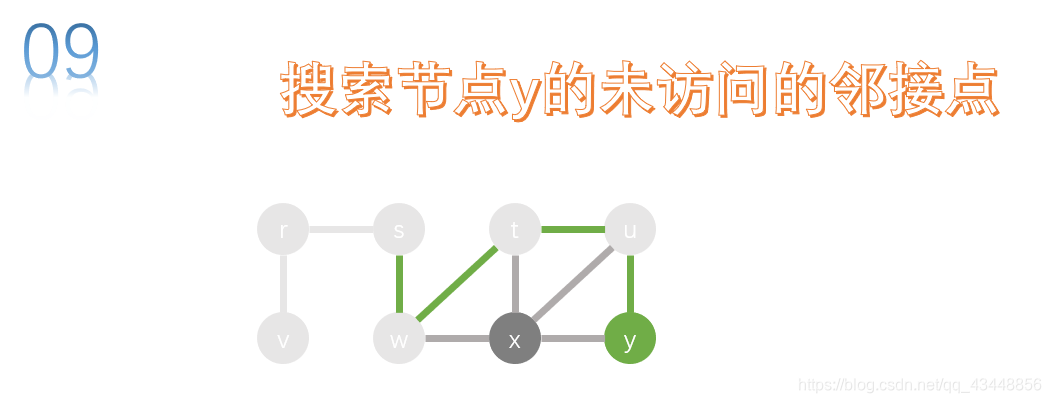
y的邻接点有x和u，u已经被访问了，所以我们对x进行搜索。
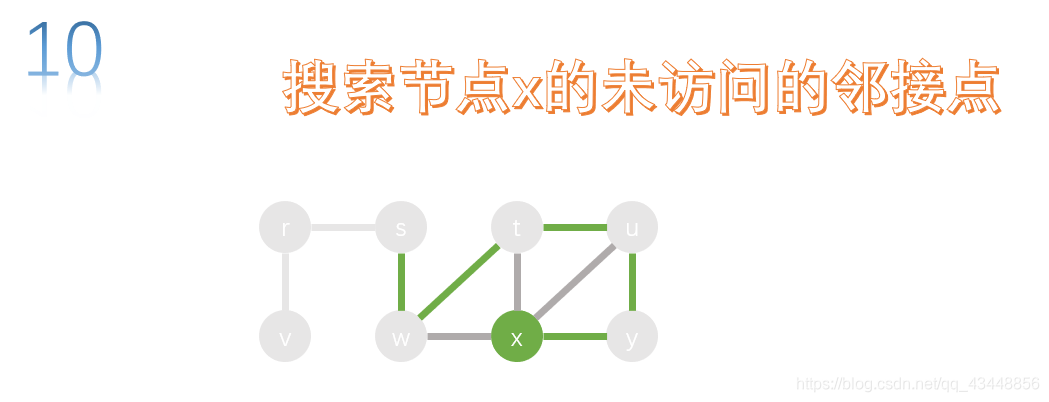
x的邻接点有w、t、u、y，都已经被访问了，所以x不能继续下去，我们九返回上一个节点，也就是返回y，对y的未访问的邻接点进行搜索。
y的所有邻接点都已经访问了，所以返回上一个节点u，对u的未访问的邻接点进行搜索。
u的所有邻接点都已经访问了，所以返回上一个节点t，对t的未访问的邻接点进行搜索。
t的所有邻接点都已经访问了，所以返回上一个节点w，对w的未访问的邻接点进行搜索。
w的所有邻接点都已经访问了，所以返回上一个节点s，对s的未访问的邻接点进行搜索。
w的所有邻接点都已经访问了，s没有上一级节点了，所以深度优先搜索也就结束了。
访问的顺序：s、r、v、w、t、u、y、x
访问的顺序与广度优先搜索会有所不同，但是它们的时间复杂度是相同的。
例题
第一题
简单模板题
#include<stdio.h>
int n,m;//数量
int num[100];//记录排列的数据序列
void recurrence(int f,int l){//DFS递归
int i,j;
if(f == m+1){//一个序列达到要求
for(i=1;i<=m;i++)//输出序列
printf("%d ",num[i]);
printf("\n");
return;//返回上一个数
}
for(i=l;i<=n;i++){//循环遍历所有没有用到的数
num[f] = i;//标记该数已经使用
recurrence(f+1,i+1);//遍历下一个数
num[f] = 0;//标记该数没有使用
}
}
int main()
{
scanf("%d %d",&n,&m);
recurrence(1,1);
return 0;
}
第二题
对是否进入下一个格子加一个条件即可。
class Solution {
public:
int n,m,k;
int cnt = 0;//记录有多少个格子
int flag[51][51];//记录x，j位置是否走过
int computer(int a){//计算数a的各位数上数字的和
int count = 0;
while (a){
count += a%10;
a /= 10;
}
return count;
}
void dfs(int x,int y){//深搜
if(computer(x)+computer(y)>k || x<0 || y<0 || x>=n || y>=m || flag[x][y]==1)//不符合条件的点跳过
return;
cnt++;//记录该点符合要求
flag[x][y] = 1;//标记点已经走过
//走上下左右四个点是否符合
dfs(x+1,y);
dfs(x,y+1);
dfs(x-1,y);
dfs(x,y-1);
}
void bfs(){
queue<pair<int,int>> q;//队列记录点的顺序
q.push({0,0});//将起始点入队列
while(!q.empty()){//循环直到点为空为止
auto a = q.front();//获取队列首
q.pop();//将队列首出队列
int x = a.first, y = a.second;
if(computer(x)+computer(y)>k || x<0 || y<0 || x>=n || y>=m || flag[x][y]==1)//不符合条件的点跳过
continue;
cnt++;//记录该点符合要求
flag[x][y] = 1;//标记点已经走过
//走上下左右四个点是否符合
q.push({x+1,y});
q.push({x,y+1});
q.push({x-1,y});
q.push({x,y-1});
}
}
int movingCount(int threshold, int rows, int cols)
{
k = threshold;
n = rows;
m = cols;
// dfs(0,0);
bfs();
return cnt;
}
};
第三题
使用dfs去模拟进站与出站，遍历所有可能并打印即可。
#include<stdio.h>
int n;//数量
int num[100],stop[100],f=0,m=0;//记录火车站栈的数据序列
int flag[100];
int cnt = 0;
void dfs(int x){//DFS递归,对进栈和出栈进行模拟
if(f>0){//出栈
num[m++] = stop[--f];
dfs(x);
stop[f++] = num[--m];
}
if(x <= n){//进栈
stop[f++] = x;
dfs(x+1);
f--;
}
if(x == n+1 && cnt < 20 && f == 0){//符合要求，打印结果
cnt++;
for(int i=0;i<n;i++)
printf("%d",num[i]);
printf("\n");
}
}
int main()
{
scanf("%d",&n);
dfs(1);
return 0;
}
第四题
数据较小，直接使用dfs暴力模拟所有情况，去最小的。但是直接使用dfs会超时，我们需要对dfs进行一些优化：
- 当缆车数已经大于等于已知的最小值时，可以直接结束该方案。
- 将猫的重量进行排序，我们从大到小进行dfs，这样可以减少组合坐车的情况。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int n,w;
int num[20], car[20];
int cnt = 20;
void dfs(int f,int k){
if(k >= cnt)//缆车数已经大于等于已知的最小缆车数
return;
if(f < 0){//猫已经全部上车
if(cnt > k)//当前方案的缆车数最小
cnt = k;
return;
}
for(int i=0;i<k;i++)//遍历所有缆车
if(car[i]+num[f] <= w){//判断是否可以合座一辆
car[i] += num[f];
dfs(f-1, k);
car[i] -= num[f];
}
car[k++] = num[f];//另外开一辆缆车
dfs(f-1, k);
k--;
}
int main()
{
scanf("%d %d",&n,&w);
for(int i=0;i<n;i++)
scanf("%d",&num[i]);
sort(num,num+n);//排序，从小到大
dfs(n-1, 0);//dfs
printf("%d",cnt);
return 0;
}
三、总结
深度优先搜索的特征为沿着一条路径不断往下，进行深度搜索。虽然广度优先搜索和深度优先搜索在搜索顺序上有很大的差异，但是在操作步骤上却只有一点不同，那就是选择哪一个候补顶点作为下一个顶点的基准不同。
广度优先搜索选择的是最早成为候补的顶点，因为顶点离起点越近就越早成为候补，所以会从离起点近的地方开始按顺序搜索；而深度优先搜索选择的则是最新成为候补的顶点，所以会一路往下，沿着新发现的路径不断深入搜索。
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
