图的术语及常用存储方式

 

 
 

  

图的术语

• 在图中的数据元素通常称做顶点，V是顶点的有穷非空集合；VR 是两个顶点之间的关系的集合。
• 若<v,ω> ∈ VR，则 <v,ω> 表示从 v 到 ω 的一条弧，且称 v 为弧头或终端点，此时的图称为有向图。如上图 G₁ 是有向图。
  G₁ = (V₁, {A₁})
  V₁ = {v₁, v₂, v₃, v₄}
  A₁ = {<v₁, v₂>, <v₁, v₃>, <v₃, v₄>, <v₄, v₁>}
• 若 <v,ω> ∈ VR 必有 <ω,v> ∈ VR，即 VR 是对称的，则以无序对 (v,ω) 代替这两个有序对，表示 v 和 ω 之间的一条边，此时的图称为无向图。如上图 G₂ 是无向图。
  G₂ = (V₂, {A₂})
  V₂ = {v₁, v₂, v₃, v₄, v₅}
  A₂ = {(v₁, v₂), (v₁, v₄), (v₂, v₃), (v₂, v₅), (v₃, v₄), (v₃, v₅)}
• 对于无向图，边的取值范围是 0 到 n(n-1)/2 。有 n(n-1)/2 条边的无向图称为完全图。
• 对于有向图，边的取值范围是 0 到 n(n-1) 。有 n(n-1) 条边的有向图称为有向完全图。
• 有很少边或者弧 (如边<nlogn) 的图称为稀疏图，反之称为稠密图。
• 有时图的边或弧具有与它相关的数，这种与图的边或弧相关的数叫做权。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网。
• 假设有两个图 G=(V, {E}) 和 G^’=(V^’, {E^’}) ，如果 V^’⊆V 且 E^’⊆E，则称 G^’ 为 G 的子图。
  
• 对于无向图 G=(V, { E })，如果边 (v, v^’)∈E，则称顶点 v 和 v^’ 互为邻接点，即 v 和 v^’ 相邻接。边 （v, v^’) 依附于顶点 v 和 v^’，或者说 (v, v^’) 和顶点 v 和 v^’ 相关联。
• 顶点 v 的度是和 v 相关联的边的数目，记为 TD(V)。例如，G₂ 中顶点 v₃ 的度是 3。对于有向图 G=(V, { A })，如果弧 <v, v^’>∈A，则称顶点 v 邻接到顶点 v^’，顶点 v^’ 邻接自顶点 v。弧 <v, v^’> 和顶点 v, v^’ 相关联。以顶点 v 为头的弧的数目称为 v 的入度，记为 ID(v)；以 v 为尾的弧的数目称为 v 的出度，记为 OD(v)；顶点 v 的度为 TD(v)=ID(v)+OD(v)。例如，图 G₁ 中顶点 v₁ 的入度 ID(v₁)=1，出度 OD(v₁)=2，度 TD(v₁)=ID(v₁)+OD(v₁)=3。一般地，如果顶点 v_i 的度记为 TD(v_i)，那么一个有 n 个顶点，e 条边或弧的图，满足以下关系
  
• 无向图 G=(V, { E }) 中从顶点 v 到顶点 v^’ 的路径是一个顶点序列 ( v=v_i,0, v_i,1, …, v_i,m=v^’ )，其中 (v_i,j-1, v_i,j)∈E，1≤j≤m。如果 G 是有向图，则路径也是有向的，顶点序列应满足 <v_i,j-1, v_i,j>∈E，1≤j≤m。路径的长度是路径上的边或弧的数目。
• 第一个顶点和最后一个顶点相同的路径称为回路或环。
• 序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。
• 在无向图 G 中，如果从顶点 v 到顶点 v^’ 有路径，则称为 v 和 v^’ 是连通的。如果对于图中任意两个顶点 v_i、v_j∈V，v_i 和 v_j 都是连通的，则称 G 是连通图。上图的 G₂ 就是一个连通图，而图中 G₁ 则是非连通图；下图 G₃ 有 3 个连通分量。所谓连通分量，指的是无向图中的极大连通子图。
  
• 在有向图 G 中，如果对于每一对 v_i,v_j∈V，v_i≠v_j，从 v_i 到 v_j 和从 v_j 到 v_i 都存在路径，则称 G 是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。例如上图中的 G₁ 不是强连通图，但它有两个强连通分量。
  
• 一个连通图的生成树是一个极小连通子图，它含有图中全部顶点，但只有足以构成一棵树的 n-1 条边。下图是 G₃ 中最大连通分量的一棵生成树。如果一颗生成树上添加一条边，必定构成一个环，因为这条边使得它依附的那两个顶点之间有了第二条路径。一棵有 n 个顶点的生成树有且仅有 n-1 条边。如果一个图有 n 个顶点和小于 n-1 条边，则是非连通图。如果它多于 n-1 条边，则一定有环。但是，有 n-1 条边的图不一定是生成树。
  
• 如果一个有向图恰有一个顶点的入度为 0，其余顶点的入度均为 1，则是一棵有向树。一个有向树的生成森林由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧。如下图
  
   
   

图的存储结构

数组表示法

  图的数组存储表示，也称为邻接矩阵。
图的邻接矩阵定义：

  上图中 G₁ 和 G₂ 的邻接矩阵如下图。

  无向图关于主对角线对称，则可采用压缩存储的方式只存入矩阵的下三角(或上三角)元素。
  借助于邻接表容易判定任意两个顶点之间是否有边(或弧)相连，并容易求得各个顶点的度。对于无向图，顶点 v_i 的度是邻接矩阵中第 i 行(或第 i 列)的元素之和，即

对于有向图，第 i 行的元素之和为顶点 v_i 的出度 OD(v_i)，第 j 列的元素之和为顶点 v_j 的入度 ID(v_i)。
 
网的邻接矩阵定义：

 
 

邻接表

  邻接表是图的一种链式存储结构。在邻接表中，对图中每个顶点建立一个单链表，第 i 个单链表中的结点表示依附于顶点 v_i 的边(对有向图是以顶点 v_i 为尾的弧)。
  每个结点由 3 个域组成，其中邻接点域(adjvex)指示与顶点 v_i 邻接的点在图中的位置，链域(nextarc)指示下一条边或弧的结点；数据域(info)存储和边或弧相关的信息，如权值等。
  每个链表上附设一个表头结点。在表头结点中，除了设有链域(firstarc)指向链表中第一个结点之外，还设有存储顶点 v_i 的名或其他有关信息的数据域(data)。

  若无向图中有 n 个顶点、e 条边，则它的邻接表需 n 个头结点和 2e 个表结点。显然，在边稀疏(e<<n(n-1)/2)的情况下，用邻接表表示图比邻接矩阵节省空间，当和边相关的信息较多时更是如此。

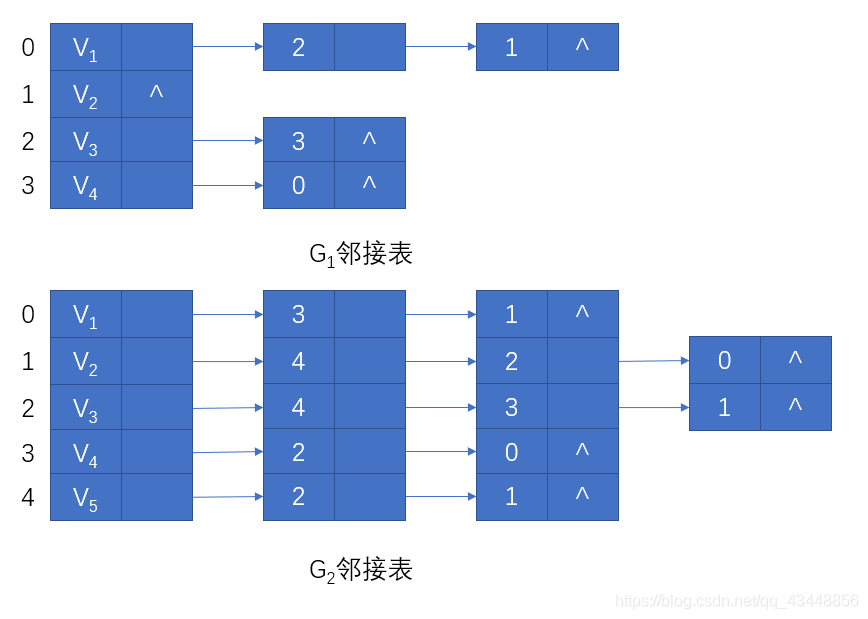
  在无向图的邻接表中，顶点 v_i 的度恰为第 i 个链表中的结点数；而在有向图中，第 i 个链表中的结点个数只是顶点 v_i 的出度，为求入度，必须遍历整个邻接表。在所有链表中其邻接点域的值为 i 的结点的个数是顶点 v_i 的入度。有时为了便于确定顶点的入度，可以建立一个有向图的逆邻接表。

  建立邻接表时间复杂度 O(n+e)，查找结点位置时间复杂度 O(n*e)。
  在邻接表上容易找到任一顶点的第一个邻接点，但要判定任意两个顶点(v_i 和 v_j)之间是否有边或弧相连，则需搜索第 i 个或第 j 个链表，因此，不及邻接矩阵方便。
 
 

十字链表

  十字链表是有向图的另一种链式存储结构。可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中，对应于有向图中每一条弧有一个结点，对应于每个顶点也有一个结点。

  弧结点：

• 尾域(tailvex)： 指示弧尾顶点位置
• 头域(headvex)： 指示弧头顶点位置
• 链域(hlink)： 指向弧头相同的下一条弧
• 链域(tlink)： 指向弧尾相同的下一条弧
• 域(info)： 指向该弧的相关信息
    弧头相同的弧在同一链表上，弧尾相同的弧也在同一链表上。

  顶点结点：

• 域(data)： 存储和顶点相关的信息，如顶点名称
• 链域(firstin)： 指向以该顶点为弧头的第一个弧结点
• 链域(firstout)： 指向以该顶点为弧尾的第一个弧结点
  
    若将有向图的邻接矩阵看成是稀疏矩阵的话，则十字链表也可以看成是邻接矩阵的链表存储结构，在图的十字链表中，弧结点所在的链表非循环链表，结点之间相对位置自然形成，不一定按顶点序号有序，表头结点即顶点结点，它们之间不是链接，而是顺序存储。
    在十字链表中既容易找到以 v_i 为尾的弧，也容易找到以 v_i 为头的弧，因而容易求得顶点的出度和入度。
    建立十字链表的时间复杂度和建立邻接表是相同的。

 
 

邻接多重表

  邻接多重表是无向图的另一种链式存储结构。
  邻接多重表的结构和十字链表类似。

  弧结点：

• mark： 标记域，可用以标记该条边是否被搜索过
• ivex和jvex： 该边依附的两个顶点在图中的位置
• ilink： 指向下一条依附于顶点 ivex 的边
• jlink： 指向下一条依附于顶点 jvex 的边
• info： 指向和边相关的各种信息的指针域

  顶点结点：

• data： 存储和该顶点相关信息
• firstedge： 指示第一条依附该顶点的边

  在邻接多重表中，所有依附于同一顶点的边串联在同一链表中，由于每条边依附于两个顶点，则每个边结点同时链接在两个链表中。
  对于无向图而言，其邻接多重表和邻接表的差别，仅仅在于同一条边在邻接表中用两个结点表示，而在邻接多重表中只有一个结点。因此，除了在边结点中增加一个标志域外，邻接多重表所需的存储量和邻接表相同。在邻接多重表上，各种基本操作的实现亦和邻接表相似。