POJ3233 Matrix Power Series（矩阵快速幂）（矩阵快速幂+等比数列二分求和取模）

首先给出题目：
Matrix Power Series
Description

Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak.

Input

The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 109) and m (m < 104). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output

Output the elements of S modulo m in the same way as A is given.

Sample Input

2 2 4
0 1
1 1
Sample Output

1 2
2 3

这个题目主要用（矩阵快速幂+等比数列二分求和取模），裸的套板子就行了
首先是矩阵快速幂
矩阵快速幂其实和我们平时的快速幂十分相似，现在只不过是换成了矩阵相乘而已，单独写一个函数封装矩阵相乘就可以了，矩阵快速幂常常应用在斐波拉契类型的题目当中。
首先给出矩阵快速幂的板子：

const int maxn=;
cosnt int mod=;
int n,k;
struct Matrix{
	int mat[maxn][maxn];
};
Matrix mul(Matrix a,Matrix b)
{
	Matrix ret;
	memset(ret.mat,0,sizeof(ret.mat));
	for(int i=1;i<=k;i++)
	{
		for(int j=1;j<=k;j++)
		{
			if(a.mat[i][j])
			{
				for(int l=1;l<=k;l++)
				{
					ret.mat[i][l]+=(a.mat[i][j]*b.mat[j][l])%mod;
				}
			}
		}
	}
	return ret;
}
Matrix M_poww(Matrix a,Matrix b)
{
	Matrix ret;
	Matrix temp=a;
	memset(ret.mat,0,sizeof(ret.mat));
	for(int i=1;i<=k;i++)
	ret.mat[i][i]=1;//注意构造的是单位矩阵
	while(b)
	{
		if(b&1)
		ret=mul(ret,temp);
		temp=mul(temp.temp);
		b>>=1;
	}
	return ret;
}

然后介绍等比数列二分求和取模:
这种方法主要是用来解决类似于等比数列的求和问题的，这样的例题在前面的博客我也写到过，但是只是一笔带过，所以现在再来写一次：
Sn= a+a^2+…+an
要求 Sn mod p（如果用公式算，可能溢出，因此用二分法求）

① 若 n是偶数
Sn= a+…+a^n/2 + a^n/2+1 + a^n/2+2 +…+ a^n/2+n/2
=(a+…+a^n/2) + a^n/2*(a+…+an/2)
=Sn/2+ a^n/2*Sn/2
=(1+a^n/2)Sn/2

②若n是奇数
Sn= a+…+a^(n-1)/2 + a^(n-1)/2+1 +…
+ a^(n-1)/2+(n-1)/2 + a^(n-1)/2+(n-1)/2 + 1
=S(n-1)/2 + a^{(n-1)/2*(a+…+a}(n-1)/2)+an
*=(1+a^(n-1)/2)S(n-1)/2+an

所以我们得到了公式：
①为偶数时：

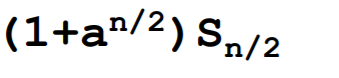
②为奇数时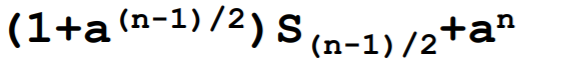
然后给出板子：
给出的是以下的：

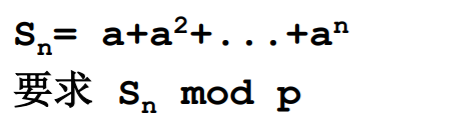
其实这样的矩阵也可以类比，最后一样代入推理即可
即照着这个写即可：
①k为偶数时 A^1+A2+…+A^k==(A1+…+A^(k/2))*A(k/2)+(A^1+…+A(k/2))
②k为奇数时 A^1+A2+…+A^k==(A1+…+A^(k/2))*A(k/2+1)+(A^1+…+A(k/2))+A^(k/2+1)

int ksm(int a,int b,int c)
{
	int res=1,base=a%c;
	while(b)
	{
		if(b&1)
		res=res*base%c;
		base=base*base%c;
		b>>=1;
	}
	return res;
}
int powsummod(int a,int n,int p)
{
	if(n==1)
	return a%p;
	if(n%2==0)
	return (1+ksm(a,n/2,p))*powsummod(a,n/2,p)%p;
	else 
	return ((1+ksm(a,(n-1)/2,p))*powsummod(a,(n-1)/2,p)+ksm(a,n,p))%p;
}

最后直接上AC代码：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdio>
using namespace std;
int n,k,mod;
const int maxn=40;
struct Matrix{
	int mat[maxn][maxn];
};
Matrix mul(Matrix a,Matrix b)
{
	Matrix ret;
	memset(ret.mat,0,sizeof(ret.mat));
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
				for(int l=1;l<=n;l++)
				{
					ret.mat[i][j]=(ret.mat[i][j]+a.mat[i][l]*b.mat[l][j])%mod;
				}
		}
	}
	return ret;
}
Matrix M_poww(Matrix a,int b)
{
	Matrix ret;
	Matrix temp=a;
	memset(ret.mat,0,sizeof(ret.mat));
	for(int i=1;i<=n;i++)
	ret.mat[i][i]=1;//注意构造的是单位矩阵
	while(b)
	{
		if(b&1)
		ret=mul(ret,temp);
		temp=mul(temp,temp);
		b>>=1;
	}
	return ret;
}
Matrix add(Matrix ta,Matrix tb)
{
	Matrix c;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			c.mat[i][j]=(ta.mat[i][j]+tb.mat[i][j])%mod;
		}
	}
	return c;
}
Matrix sum(Matrix a,int n)
{
	Matrix ta,tb;
	if(n==1)
	return a;
	ta=sum(a,n/2);
	if(n%2==0)
	{
		tb=M_poww(a,n/2);
		return add(mul(tb,ta),ta);
    }
	else
	{
		tb=M_poww(a,n/2+1);
		ta=add(mul(tb,ta),ta);
		return add(ta,tb);
	}
}
int main()
{
	int tt;
	while(~scanf("%d%d%d",&n,&k,&mod))
	{
		struct Matrix temp,ans;
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				scanf("%d",&tt);
				temp.mat[i][j]=tt%mod;
			}
		}
		ans=sum(temp,k);
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				printf("%d",ans.mat[i][j]);
				if(j!=n)
				printf(" ");
			}
			printf("\n");
		}
	}
	return 0;
}

完啦~~~