一、数学
1.基础
1.1有理数和无理数
常见的无理数
π、e(=2.718...)、√2、√3、√5、√10、√99、㏒2^3
建议记下
√2 = 1.414...
√3 = 1.732...
√5 = 2.236...
√10 = 3.162...
无理数即无线不循环小数。
有理数都能用分数表示。
无线循环小数可以用分数表示,因此是有理数:
x=0.2323...
100x=23.2323...
99x=23
x=23/99
两个有理数加减乘除,结果一定是有理数(除数是0除外:0可以作为被除数不能作为除数)。
无理数和有理数(除了0)加减乘除,还是无理数,除了√2*0、0/√2这种情况。
无理数之间的加减乘除,不确定,如√2-√2是有理数、√2+√2还是无理数。
化简:
3x-√5x-2y+4√5y-4-2√5 = 0
3x-2y-4-√5x+4√5y-2√5 = 0
(3x-2y-4) - (√5x-4√5y+2√5) = 0
(3x-2y-4) - √5(x-4y+2) = 0
x-4y+2 = 0 3x-2y-4 = 0
x-4y+2-3x+2y+4 = 0
-2x-2y+6 = 0
-2x-2y = -6
-2(x+y) = -6
x+y = 3
x=3-y
x-4y+2 = 0 3-y-4y+2 = 0 5-5y = 0 y = 1
x = 2
结果:x=2,y=1
1.2自然数
假设该自然数为x,则√x = a,x=a^2 ,相邻的两个自然数:a^2-1、a^2+1
相邻的两个自然数的算数平方根:√(a^2-1)、√(a^2+1)
1.3整除&公约数公倍数
如6和9。
互为质数:两个数除了1之外没有别的公约数,如3和5,则3和5互为质数。
质数:在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
2和6的最大公约数是2、最小公倍数是6。
快速找到两个自然数的最大公约数和最小公倍数,短除法:
16和24的最大公约数:2*2*2=8
最小公倍数:2*2*2*2*3=48
对于求3个自然数的最大公约数和最小公倍数,采用短除法的注意事项:
——(2 5 8的时候,2、8还可以再约、此时为了求得正确的最小公倍数,应继续对2、8约分,对5要照抄保留!)
12、30、48的最大公约数:2*3=6
最小公倍数:2*3*2*1*5*4=240
至少可以剪出几个就是要先求出90、42的最大公约数,为6;
90/6=15个/行
42/6=7个/列
所以是15*7=105个
能被2整除的数的特征:2的1次方等于2,所以末位能被2整除的数是能被2整除的数。
能被4整除的数的特征:2的2次方等于4,所以末2位能被4整除的数是能被4整除的数。
能被8整除的数的特征:2的3次方等于8,所以末3位能被8整除的数是能被8整除的数。
能被16整除的数的特征:2的4次方等于16,所以末4位能被16整除的数是能被16整除的数。
能被125整除的数:125、250、375、500、675、750、875、1000
能被9整除的数的特征:每个位上的数的和能被9整除,该数就是9的倍数。
能被11整除的数:奇数位之和与偶数位之和的差能被11整除。能被9整除的数的特征:每个位上的数的和能被9整除,该数就是9的倍数。推理:
对于某数wxyz,如果能被9整除。则有w*10000+x*1000+10*y+z = 9*n,继续推理,
(x+y+z) + (w*9999+x*999+9*y) = 9*n,因为(w*9999+x*999+9*y)可以被9整除,所以(x+y+z)也可以被9整除,所以每个位上的数的和能被9整除的数,该数是9的倍数。
45*x = 67□8□
5*9*x = 67□8□
67□8□是5的倍数 => 67□80、67□85
67□8□是9的倍数 => 67□80、67□85是9的倍数 =>
对于67□80,6+7+x+8+0=9*n,x=6 => 67680
对于67□85,6+7+x+8+5=9*n,x=1 => 67185
所以:67680、67185
1.4奇数和偶数

和差同性是指任意两个数的和如果是奇数,那么差也是奇数;如果和是偶数,那么差也是偶数。
根据和差同奇偶、以及偶-偶、奇-奇都是偶数,推出差不可能是5。
两个条件单独都充分,条件判断题选D。
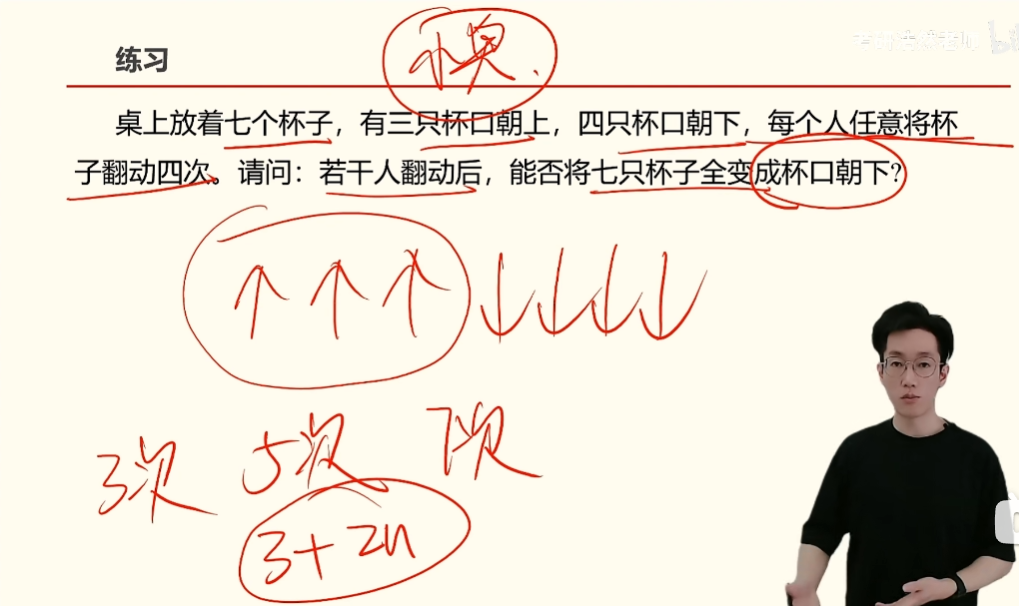
必须翻动3+2n=奇数次才能全部杯口朝下,4是偶数,所以答案是不能。
1.5质数和合数
质数和合数的范围:> 1的整数不是质数就是合数(1既不是质数也不是合数)

![]()

对539进行分解质因数:7*7*11
1.6比与比例


b:a = 3:4 c:b = 4:5
a:b=1/3:4/1 b:c=1/4:1/5
a:b:c = 1/3:4/1:1/5 = (1/3)*60:(4/1)*60:(1/5)*60 = 20:15:12
1m+1.5m+2.5m=1000
5m=1000
m=200
(1/2:1/3:1/9)*18 = 9:6:2
34/(9+6+2)=34/17=2万
2*9=18万
正比例(量变比值一定),简称正比,是指两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值(或者说商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。如2支笔8 元,7支多少钱?就有等式:2:7=8:X(这就是正比例),解这比例:X=7*8/2=28(元)
反比例(量变乘积一定),指的是两种相关联的变量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,那么他们就叫做成反比例的量,他们的关系叫做反比例关系。反比例的例子 简介 1、百米赛跑,路程100米不变,速度和时间是反比例;2、排队做操,总人数不变,排队的行数和每行的人数是反比例;
圆的面积和它的半径 A. 成正比例 B. 成反比例 C. 不成比例S/r=πr, 虽然π是定量,但r是变量,所以圆周率×半径的积就不一定, 所以圆的面积和它的半径量变比值(πr)不一定,不成正比例关系;Sr=πr^3,所以圆的面积和它的半径量变乘积(πr^3)不一定,也不成反比例关系。
故选:C. 圆的面积只是与半径的平方成正比例关系,和半径不成比例关系。
注意:(a+c) / (b+d)不能推出a/b = c/d,反之才可以。如:
(1+2) / (3+7)不能推出1/3 = 2/7,1/3 != 2/7
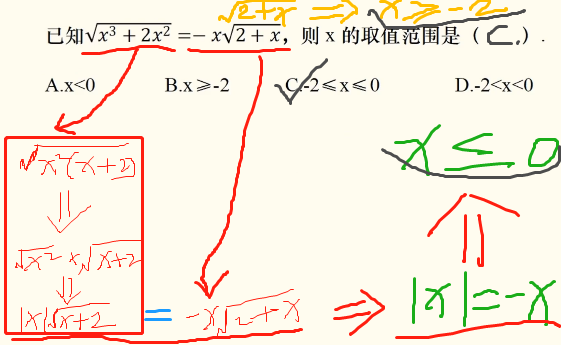
1.7绝对值
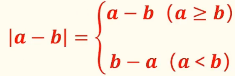
取并集。
x<1时】,y = 1-x+2-x = 3-2x,y = 【3-2x
1=<x<=2时】,y = x-1+2-x= 1,y = 【1
x>1时】,y = x-1+x-2 = 2x-3,y = 【2x-3
第一步:找到临界点、1和-2。即 __-4____-3____-2____-1____0____1____2____3__
即X<-2、-2<=X<=1、X>1。
第二步:
X<-2: (1-x) - |x - (-2)| < 2 => 1-x - (-2 - x) < 2 => 1-x+2+x < 2 3<2 不成立,所以!(x<-2)
-2<=X<=1: 1-x-(x+2) < 2 => 1-x-x-2) < 2 => -2x-1<2 => -2x<3 => x>-(3/2)
所以-2<=X<=1时需要x>-1.5题干中不等式才成立
X>1: x-1-x-2<2 => -3<2 成立,所以x>1可以使题干中不等式成立
综上所述:取x>-1.5、x>1的并集即可,所以x>-1.5
2022管综条件充分性判断真题:
由|x-2| - |x-3| = a,找到临界点2、3并解等式:
x<2 => a=-1
x>3 => a=1
2<=x<=3 => a=2x-5
关键一步,根据解析的等式/方程,画函数图像(a值相当于y轴刻度值):
当0<a<0.5(即y轴取0到0.5不包括0和0.5时),有唯一的x轴刻度值与a值对应。
当a=1时(即y轴取1时),没有唯一的x轴刻度值与a值对应,x可以取>=3的任意值,因此不能确定x是哪一个值。
故,第一个条件是充分的,第二个条件是不充分的。选A。
已知的3个公理:
;√ab = √a√b;根号下的值>=0;
乍一看很复杂,其实:
|a-3| >= 0
√3b+5 >= 0 4开方是±2,4的平方根表示法:±√4=±2,平方根又叫二次方根;4的算术平方根表示法:√4=2;
(5c-4)^2 >= 0
3个>=0的数相加 = 0,所以三个数一定都等于0。
a=3、b=-5/3、c=4/5
abc = -15/3*4/5 = -5*4/5 = -4
三种情况:x<-1时,最大值是-3;-1<=x<=2时,取值是[-3,3]最大值是3;x>2时,最大值是3
所以最大值是3
1.8浓度问题
方法1列方程,设需要x克:(300*95%+60%x) / (300+x) = 75%
方法2交叉法(仅适用于浓度类似题型):
95% |60-75|=15
75%
60% |90-75|=20
15/20 => 3/4 【3:4即为95%浓度酒精和60%浓度酒精混合为75%浓度酒精的混合比例】
左图描述的是A、B溶液混合成28%浓度溶液配置的比例。
80g
浓度问题的类比问题:
30人
方法1:最后的溶液质量不变还是100g,只需要获得最后的溶质多少g即可求出最后的盐水浓度。刚开始100g*80%=80g盐,然后倒出了80g*(40g/100g)= 80g*0.4 =32g盐,还剩48g盐,继续类推即可。
方法2:最后的溶液质量不变还是100g,溶液 = 溶质 / 溶度;因为溶质在每次倒出后都减少40%,也就是每次新溶质都是旧溶质*0.6;又因为溶液 = 溶质 / 溶度成正比例 且 每次倒出再倒满后溶液不变,所以溶质作为分子*0.6时,溶度作为分母也*0.6。所以反复三次后最终浓度是80%*0.6^3 = 0.8*0.6*0.6*0.6 = 0.48*0.36 = 17.28%
解方程消y即可得x:
5x+6y=7.7 5x+2y=5.6 => 15x+6y=16.8
15x+6y-5x-6y = 16.8-7.7 => 10x=9.1 => x=0.91=91%
方法1列方程:
设原来盐水xkg,每次加入ykg水,原来的溶质为zkg,则原来盐水浓度为z/x,且有:
3% = z / (x+y) => z = (x+y)*0.03 = 0.03x+0.03y
2% = z / (x+2y) => z = (x+2y)*0.02 = 0.02x+0.04y
即0.03x+0.03y = 0.02x+0.04y => 3x+3y = 2x+4y => x=y
因为x=y且 z = 0.03x+0.03y,所以z = 0.06x,则原来盐水浓度为z/x = 0.06 = 6%
方法2比例(盐的质量即溶质是不变的):
第一次加水后浓度3%:当盐3kg时,盐水100kg => 当盐6kg时,盐水200kg
第二次加水后浓度2%:当盐2kg时,盐水100kg => 当盐6kg时,盐水300kg
因为盐的质量即溶质是不变的,所以每次加水300-200=100kg,所以加水前的盐水为100kg,则溶质是6kg/100kg=6%
1.9其他相关应用题

2.整式与分式
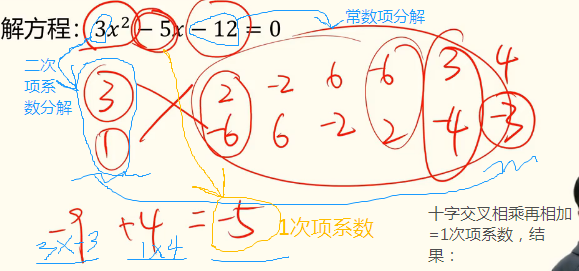
2.1十字相乘法
解得x=3或者x=-4/3
x = 2或3或-2或-3
2.2乘法公式

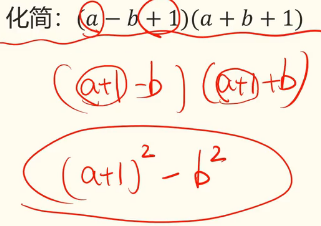
方法1
方法2
真题:
方法1:
(x+y)(x-y)-(x-y)+1
(x-y)(x+y-1)+1
方法2:
(1)x^2 - x^2-x+x+1 = 1
(2)(1-y)^2 - y^2 -1 + y + y + 1
1+y^2-2y -y^2-1+2y+1 = 1
2.3配方
结果:x = (-b±√(b^2-4ac)) / (2a)
ax^2 + bx + c = 0 a(x^2 + (b/a)x) + c = 0
a(x^2 + (b/a)x + b^2/(4a^2)) - b^2/(4a) + c = 0 a(x + b/(2a))^2 = (b^2 - 4ac)/(4a)
(x + b/(2a))^2 = (b^2 - 4ac)/(4a^2) 若要此方程有解,需要a != 0且b^2 - 4ac >= 0
x+b/(2a) = ±√(b^2 - 4ac) / (2a) x = (-b±√(b^2-4ac)) / (2a)
一次项系数一半的平方
x^2 - 5x -3 = 0 x^2 - 5x -3 + (5/2)^2 - (5/2)^2 = 0 (x-5/2)^2 - 3 - (5/2)^2 = 0
(x-5/2)^2 = 3 + 25/4 (x-5/2)^2 = 37/4 x-5/2 = ±√37/2 x = (5 ± √37)/2
x^2 - 2x + 1 + 1 = 0 (x-1)^2 = -1 无解、平方数不可能为负数
化简:
√((√2^2 + √3^2) + 2√6) √(√2^2 + √3^2 + 2√2√3) √(√2+√3)^2 √2+√3
√(7-2*2√3) √(7-2*√4*√3) √(7-2*√12) √(√3^2+√4^2 - 2*√12)
√(√3^2+√4^2 - 2*√(3*4)) √(√3^2+√4^2 - 2*√3*√4)) √(√3-√4)^2 或者 √(√4-√3)^2
即√3-√4 或者 √4-√3
因为√下的数字必须>=0,所以最终结果是√4-√3
结果5√2-7
且
即x^2 + 1/x^2 = (x +1/x)^2 - 2
x^3 + 1/x^3 = x^3 + (1/x)^3
= (x + 1/x)(x^2 + 1/x^2 - 1) = 3(x^2 + 1/x^2 - 1)
= 3((x +1/x)^2 - 2 - 1)= 3(3^2-3)
= 3*6 = 18
推出x+1/x=3,求x^3 + 1/x^3,和上题一样,结果是18
2.4分式
a^m * a^n = a^(m+n) a^m / a^n = a^(m-n)
(a^m)^n = a^(m*n)
以上为定理,请记住。
2.5工程问题

50个。
设工作量为1 甲班效率为1/12 乙班效率为1/15 甲乙共同效率1/12+1/15=3/20
已工作量为3/20 * 4天=3/5 剩余未完成工作量为1-3/5=2/5
工作时间=工作量/工作效率 (2/5) / (1/15) = 6天
方法1
设工作量为1,原工期为x
则原效率为1/x,之后效率为(1/x)*1.2即1.2/x,剩余工期为x-3-2即x-5天
原效率工作3天,之后效率工作x-5天
则(1/x)*3 + (1.2/x)*(x-5) = 1,解得x=15
方法2
设工作量为1,原效率为x
则已完成工作量3x,剩余工作量1-3x,提升后的效率为1.2x,原计划工期为1/x天
(1-3x) / 1.2x = 原计划工期-3-2 (1-3x) / 1.2x = 1/x-3-2 解得x=15
3.简单函数
3.1一次函数
一次函数是数学中经常使用的一种函数形式,可以被用来描述线性关系,如速度与时间之间的关系。一次函数可以表示为y = mx + b的形式,其中m和b是常数。
3.2二次函数
函数图像是抛物曲线形式,描述非线性关系。
对称轴是x = -b/(2a),可根据对称轴x值(顶点坐标的x值)求出y值(顶点坐标的y值)。
a>0时抛物线开口向上,a<0时抛物线开口向下
c值决定抛物线与y轴的交点值
零点的概念:函数值y=0时,x的值即为零点。二次函数的零点个数(2或者1或者0)
△ = b^2-4ac
△>0时,抛物线与x轴2个交点,ax^2 + bx + c = 0有两个不同的根/解
△=0时,抛物线与x轴1个交点,ax^2 + bx + c = 0有两个相同的根/解
△<0时,抛物线与x轴0个交点,ax^2 + bx + c = 0无解/根
a<0时,开口向下,y必然有<0的情况
a>0 且 △ = b^2-4ac < 0
韦达定理变换
x1^2 + x2^2 = (x1 + x2)^2 - 2x1x2 = (-b/a)^2 - 2c/a
|x1-x2| = √(x1 - x2)^2 = √((x1+x2)^2 - 4x1x2) = √((-b/a)^2 - 4c/a)
3.3不等式

均值不等式 推导基础 (a-b)^2 >= 0 a^2 + b^2 - 2ab >= 0 a^2 + b^2 >= 2ab
设a^2 = x,b^2 = y 则x >= 0,y >= 0 且a = √x,b = √y
因为a^2 + b^2 >= 2ab
所以x + y >= 2√(xy) 其中x >= 0,y >= 0 且x=y时,(a-b)^2 >= 0取最小值 即 x + y >= 2√(xy) 取最小值,若x != y则x + y >= 2√(xy)不能取等!
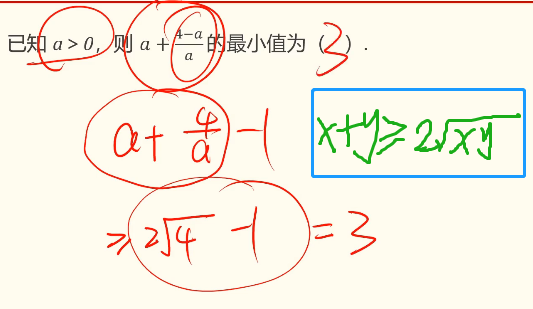
对勾函数值永远大于等于2。
选B。
3.4集合
区间法 和 图示法
3 <= x < 10
区间法: [3, 10)
图示法: 空心、实心、阴影、闭口的/左开口的/右开口的/左右开口的

如果集合A是集合B的子集,并且集合B不是集合A的子集,那么集合A叫做集合B的真子集。
空集是任意集合的子集。
并集:
交集:
全集:
一般的,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,通常记作U。
补集:
若给定全集U,有A⊆U,则A在U中的相对补集称为A的绝对补集(或简称补集),写作∁UA。
3.5应用题-容斥问题

34人。
4.排列组合
1.加法与乘法原理


2.排列与组合
...ing













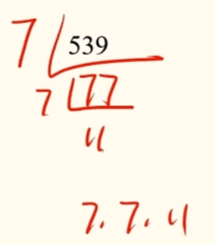














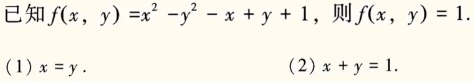









































































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








