蚁群算法（独辟蹊径的进化算法）

最新推荐文章于 2025-03-22 13:18:30 发布

山语山

最新推荐文章于 2025-03-22 13:18:30 发布

阅读量1.7k

点赞数 25

文章标签：算法开发语言 matlab 数据结构

本文链接：https://blog.csdn.net/qq_43556680/article/details/144394662

版权

蚁群算法也是一种生物仿生算法，它是通过模拟自然界中蚂蚁集体寻径行为而提出的一种基于种群的启发式随机搜索算法。自然界常理，蚂蚁可以通过群体行动在没有任何提示下从家找到食物源的最短路径，并能随着环境变化不断调整适应性地搜索出新的路径产生新的选择使得找到的路径最短。一般来说每个蚂蚁可以看成是独立的个体，相互交流的纽带是通过释放分泌信息素来实现的，所以这也是该算法模拟的核心地方，根据信息素的浓度进行下一个最优移动方向的选择，从而做到周游所有地点的最短路径，具体过程下面详述：
在这里插入图片描述

通俗认识

蚂蚁在寻找食物时会在走过的路径上释放分泌物信息素，随着时间的推移，信息素会挥发，毕竟本质是化学物质
后来的蚂蚁选择该路径的概率会与该路径上的信息素浓度成正比，群体行为而不是走不寻常的路
当在一条路径上的蚂蚁越来越多时，留下的信息素也越来越多，后来蚂蚁选择该路径的概率也就越来越大，从而又反向增加了该条路径上信息素的浓度，这就形成了正反馈机制，所以蚂蚁最终可以发现最短路径即浓度最高大家都走的那条路径，生物的行为本质是会向着少做无用功的路上奋斗的
信息素更新方式有两种，第一种是挥发，即路径上的信息素以一定的比率减少，二是增强即有蚂蚁走过释放了信息素
蚂蚁在向下一个目标的运动是通过一个随机规则实现的，这个随机规则和信息素浓度相关，需要用公式计算这个概率，并按此概率实现一次移动

一些约定

在这里插入图片描述

在这里插入图片描述
信息素更新方式

这里的信息素更新思想需要着重解释一下，并不是每只蚂蚁从城市i到城市j走过之后就立即更新，
而是要等所有的蚂蚁把所有的n个城市都遍历一遍(因为有禁忌表，不会存在重复遍历)后，才计
算所有道路的累积的信息素更新。

城市i到城市j的信息素为
在这里插入图片描述
其中，令

此时

为一次完整迭代时(一次迭代时间为城市数量n，即需要遍历完所有的城市后才计算信息素更新)在边ij所产生的信息素，这里就又涉及到一个问题，每只蚂蚁在城市i到j走过后信息素变化

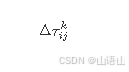
怎么计算，为此文献中有几种方法，即
在这里插入图片描述

算法步骤

1、初始化参数，时间t=0，循环次数Nc = 0，设置最大循环次数G(一般100~500)，m个蚂蚁置于n个城市，令每条边ij的初始化信息素量为

初始时刻的信息素

增量为0
2、做循环 Nc = Nc + 1
3、设置当前蚂蚁k的索引号k=1
4、将蚂蚁k此时的起点城市加入禁忌表

中，然后蚂蚁k依据城市切换概率公式选择城市j前进，然后将j加到蚂蚁k的禁忌表中
第四步不断循环且t=t+1，直到蚂蚁k完成周游即t>n，禁忌表为所有城市后结束，禁忌表此时的长度为n已满
选择下一个蚂蚁，设置当前蚂蚁k的索引号k=k+1 重复四步，直到周游(三、四步可以并行执行，即其他蚂蚁也可以同时前进)
所有蚂蚁都周游完后，即k>m后，记录本次最短的路线长度(即信息素最浓的周游遍历长度)
根据公式更新下一次迭代的每条路径的信息量
清空每只蚂蚁的禁忌表，更新迭代，直到当且迭代次数Nc大于最大循环次数G
此时最短的路线长度一定是信息素最浓的周游遍历长度

代码实现

下面是蚁群算法机器人最短路径规划问题的MATLAB代码

（1代表障碍物）

function main() 
G=[0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0; 
   0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
   0 1 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 0; 
   0 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0; 
   1 1 1 1 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0; 
   1 1 1 1 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0; 
   0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0; 
   0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0;];
MM=size(G,1);                  	   % G 地形图为01矩阵，如果为1表示障碍物 
Tau=ones(MM*MM,MM*MM);        % Tau 初始信息素矩阵
Tau=8.*Tau; 
K=100;                       	   %迭代次数（指蚂蚁出动多少波）
M=50;                        	   %蚂蚁个数
S=1 ;                         	   %最短路径的起始点
E=MM*MM;                        %最短路径的目的点
Alpha=1;                      	   % Alpha 表征信息素重要程度的参数
Beta=7;                       	   % Beta 表征启发式因子重要程度的参数
Rho=0.3 ;                      	   % Rho 信息素蒸发系数
Q=1;                               % Q 信息素增加强度系数 
minkl=inf; 
mink=0; 
minl=0; 
D=G2D(G); 
N=size(D,1);               %N表示问题的规模（象素个数）
 a=1;                     %小方格象素的边长
 Ex=a*(mod(E,MM)-0.5);    %终止点横坐标
 if Ex==-0.5 
Ex=MM-0.5; 
end 
Ey=a*(MM+0.5-ceil(E/MM)); %终止点纵坐标
 Eta=zeros(N);             %启发式信息，取为至目标点的直线距离的倒数
 %以下启发式信息矩阵
 for i=1:N 
 ix=a*(mod(i,MM)-0.5); 
   if ix==-0.5 
   ix=MM-0.5; 
   end 
iy=a*(MM+0.5-ceil(i/MM));  
   if i~=E 
   Eta(i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5; 
   else 
   Eta(i)=100; 
   end 
end 
ROUTES=cell(K,M);     %用细胞结构存储每一代的每一只蚂蚁的爬行路线
PL=zeros(K,M);         %用矩阵存储每一代的每一只蚂蚁的爬行路线长度
                      %启动K轮蚂蚁觅食活动，每轮派出M只蚂蚁
for k=1:K 
for m=1:M 
%状态初始化
W=S;                  %当前节点初始化为起始点
Path=S;                %爬行路线初始化
PLkm=0;               %爬行路线长度初始化
TABUkm=ones(N);       %禁忌表初始化
TABUkm(S)=0;          %已经在初始点了，因此要排除
DD=D;                 %邻接矩阵初始化
%下一步可以前往的节点
DW=DD(W,:); 
DW1=find(DW); 
for j=1:length(DW1) 
   if TABUkm(DW1(j))==0 
      DW(DW1(j))=0; 
  end 
end 
LJD=find(DW); 
Len_LJD=length(LJD);%可选节点的个数
%蚂蚁未遇到食物或者陷入死胡同或者觅食停止
while W~=E&&Len_LJD>=1 
%转轮赌法选择下一步怎么走
PP=zeros(Len_LJD); 
for i=1:Len_LJD 
    PP(i)=(Tau(W,LJD(i))^Alpha)*((Eta(LJD(i)))^Beta); 
end 
sumpp=sum(PP); 
PP=PP/sumpp;%建立概率分布
Pcum(1)=PP(1); 
  for i=2:Len_LJD 
  Pcum(i)=Pcum(i-1)+PP(i); 
  end 
Select=find(Pcum>=rand); 
to_visit=LJD(Select(1)); 
%状态更新和记录
Path=[Path,to_visit];       		 %路径增加
PLkm=PLkm+DD(W,to_visit);    %路径长度增加
W=to_visit;                   %蚂蚁移到下一个节点
   for kk=1:N 
      if TABUkm(kk)==0 
      DD(W,kk)=0; 
      DD(kk,W)=0; 
      end 
   end 
TABUkm(W)=0;				%已访问过的节点从禁忌表中删除
 DW=DD(W,:); 
DW1=find(DW); 
for j=1:length(DW1) 
    if TABUkm(DW1(j))==0 
       DW(j)=0; 
    end 
  end 
LJD=find(DW); 
Len_LJD=length(LJD);%可选节点的个数
 end 
%记下每一代每一只蚂蚁的觅食路线和路线长度
 ROUTES{k,m}=Path; 
   if Path(end)==E 
      PL(k,m)=PLkm; 
      if PLkm<minkl 
          mink=k;minl=m;minkl=PLkm; 
      end 
   else 
      PL(k,m)=0; 
   end 
end 
%更新信息素
Delta_Tau=zeros(N,N);%更新量初始化
   for m=1:M 
     if PL(k,m)  
        ROUT=ROUTES{k,m}; 
        TS=length(ROUT)-1;%跳数
         PL_km=PL(k,m); 
        for s=1:TS 
          x=ROUT(s); 
          y=ROUT(s+1); 
          Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km; 
          Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km; 
        end 
     end 
  end 
Tau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分，新增加一部分
 end 
%绘图
plotif=1;%是否绘图的控制参数
 if plotif==1 %绘收敛曲线
    minPL=zeros(K); 
   for i=1:K 
     PLK=PL(i,:); 
     Nonzero=find(PLK); 
     PLKPLK=PLK(Nonzero); 
     minPL(i)=min(PLKPLK); 
   end 
figure(1) 
plot(minPL); 
hold on 
grid on 
title('收敛曲线变化趋势'); 
xlabel('迭代次数'); 
ylabel('最小路径长度'); %绘爬行图
figure(2) 
axis([0,MM,0,MM]) 
for i=1:MM 
for j=1:MM 
if G(i,j)==1 
x1=j-1;y1=MM-i; 
x2=j;y2=MM-i; 
x3=j;y3=MM-i+1; 
x4=j-1;y4=MM-i+1; 
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); 
hold on 
else 
x1=j-1;y1=MM-i; 
x2=j;y2=MM-i; 
x3=j;y3=MM-i+1; 
x4=j-1;y4=MM-i+1; 
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]); 
hold on 
end 
end 
end 
hold on 
title('机器人运动轨迹'); 
xlabel('坐标x'); 
ylabel('坐标y');
ROUT=ROUTES{mink,minl}; 
LENROUT=length(ROUT); 
Rx=ROUT; 
Ry=ROUT; 
for ii=1:LENROUT 
Rx(ii)=a*(mod(ROUT(ii),MM)-0.5); 
if Rx(ii)==-0.5 
Rx(ii)=MM-0.5; 
end 
Ry(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM)); 
end 
plot(Rx,Ry) 
end 
plotif2=0;%绘各代蚂蚁爬行图
if plotif2==1 
figure(3) 
axis([0,MM,0,MM]) 
for i=1:MM 
for j=1:MM 
if G(i,j)==1 
x1=j-1;y1=MM-i; 
x2=j;y2=MM-i; 
x3=j;y3=MM-i+1; 
x4=j-1;y4=MM-i+1; 
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); 
hold on 
else 
x1=j-1;y1=MM-i; 
x2=j;y2=MM-i; 
x3=j;y3=MM-i+1; 
x4=j-1;y4=MM-i+1; 
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]); 
hold on 
end 
end 
end 
for k=1:K 
PLK=PL(k,:); 
minPLK=min(PLK); 
pos=find(PLK==minPLK); 
m=pos(1); 
ROUT=ROUTES{k,m}; 
LENROUT=length(ROUT); 
Rx=ROUT; 
Ry=ROUT; 
for ii=1:LENROUT 
Rx(ii)=a*(mod(ROUT(ii),MM)-0.5); 
if Rx(ii)==-0.5 
Rx(ii)=MM-0.5; 
end 
Ry(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM)); 
end 
plot(Rx,Ry) 
hold on 
end 
end 
function D=G2D(G) 
l=size(G,1); 
D=zeros(l*l,l*l); 
for i=1:l 
    for j=1:l 
        if G(i,j)==0 
            for m=1:l 
                for n=1:l 
                    if G(m,n)==0 
                        im=abs(i-m);jn=abs(j-n); 
                        if im+jn==1||(im==1&&jn==1) 
                        D((i-1)*l+j,(m-1)*l+n)=(im+jn)^0.5; 
                        end 
                    end 
                end 
            end 
        end 
    end 
end

效果：
在这里插入图片描述
最短路径长度稳定在38。

特点

本质上是并行算法，每个蚂蚁搜索过程中彼此独立，仅通过信息素通信，使得算法可靠性和全局搜索能力增强
自适应性，没有外界条件的预先设定和干扰，而是使得系统从无序到有序的变化过程
较强鲁棒性，求解对初始路线的要求不高，搜索过程不需要人工调整，控制参数较少，易于应用到组合优化问题的求解上
具有之前分析的正反馈性，在一定程度上使得结果更加精准。
蚁群算法用来解决最短路径问题，并真的在旅行商问题（TSP，一个寻找最短路径的问题）上取得了比较好的成效。目前，也已渐渐应用到其他领域中去，在图着色问题、车辆调度问题、集成电路设计、通讯网络、数据聚类分析等方面都有所应用。