行列式

行列式的一个几何意义是测度一个给定区域在经过特定的线性变换后面积放大或缩小的比例。使用如下矩阵对空间进行线性变换。那么对于二维空间基底
i
^
\hat{i}
i^和
j
^
\hat{j}
j^围成的正方形,在缩放前后面积变换的大小可以在图中直观的看出来。
[
3
0
0
2
]
\left[ \begin{array}{c} 3 & 0 \\ 0 & 2 \\ \end{array}\right]
[3002]
 |  |
|---|
这个缩放的比例,即线性变换改变面积的比例被称为这个变换的行列式,表示为:
det
(
[
3
2
0
2
]
)
=
6
\det \left ( \left[ \begin{array}{c} 3 & 2 \\ 0 & 2 \\ \end{array} \right ] \right) = 6
det([3022])=6
而如果一个线性变换的行列式为0,说明这个变换将平面压缩到了一条直线,甚至是一个点上。这也就是说,我们只需要检测一个线性变换的行列式是否为零就可以知道这个矩阵所代表的的变化是否将空间压缩到了更低的维度上。

另外,行列式的计算结果也可以是负数。初始状态, i ^ \hat{i} i^在 j ^ \hat{j} j^的左侧,如果变换后 j ^ \hat{j} j^出现在了 i ^ \hat{i} i^的右侧,那么这个线性空间就像是被翻转了,这事得到的行列式值为负。(可以类比于一张纸,我们定义了正面和反面,现在我们将纸翻了过去)

在三维空间中,行列式代表的是一个特定变换对体积的缩放比例。那么如下图所示,我们可以给出矩阵的列线性相关的几何解释。对于 3 × 3 3 \times 3 3×3矩阵而言,它的每一列代表变换后的基底的位置,如果三个变换后的基底共面了那么这个三维空间就被压缩成了更低维度的空间。也可以说,我们无法仅由这三个向量张成整个三维空间了。
解释:在变换之前,三个基底,有一个公共点(原点)和三个各自的终点,四个点不在同一平面内,那么通过任意的线性组合可以得到一个完整的三维空间,而变换后的三个基底落在了同一平面内,显然无法张成一个完整的三维空间。

三维空间下行列式值为负的定义。在描述三维空间的定向时,我们规定使用右手定则,即食指代表 i ^ \hat{i} i^,中指代表 j ^ \hat{j} j^,拇指代表 k ^ \hat{k} k^。如果在变换后仍然可以这样表示三个基底的方向,那么行列式的值就是正的,而如果在变换后需要使用左手进行表示,那么行列式的值为负。
 |  |
|---|
行列式计算面积的示意图。

逆矩阵、列空间和零空间

我们可以用下面矩阵乘法的方式表达左边的线性方程组。在几何解释上就是,寻找一个向量 x → \overrightarrow{x} x经过 A A A的变换后与 v → \overrightarrow{v} v重合。
A
x
→
=
v
→
A \overrightarrow{x} = \overrightarrow{v}
Ax=v
求解该问题时,结合上一部分容易想到有两种情况,(1)线性变换
A
A
A作用于空间后,空间仍保持现有维度,即
det
(
A
)
≠
0
\det(A) \neq 0
det(A)=0;(2)线性变换
A
A
A作用于空间后,空间被压缩到低维度,即
det
(
A
)
=
0
\det(A) = 0
det(A)=0。
 | 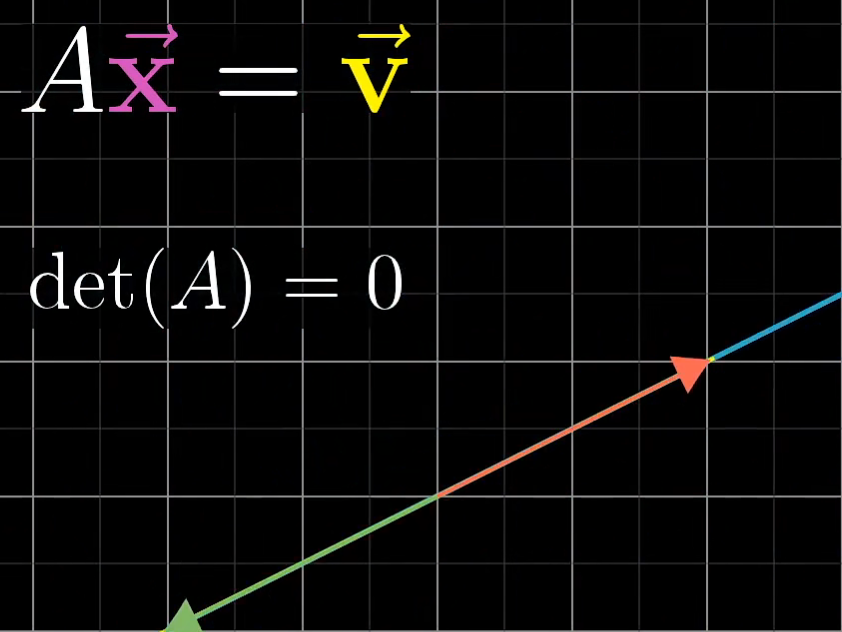 |
|---|
det ( A ) ≠ 0 \det(A) \neq 0 det(A)=0 / 逆矩阵
第一种情况的概率似乎要大一些。这种情况下,求解 x → \overrightarrow{x} x可以应用一下逆向思维。 A x → = v → A \overrightarrow{x} = \overrightarrow{v} Ax=v从左向右看是对 x → \overrightarrow{x} x进行让变换后的 x → \overrightarrow{x} x与 v → \overrightarrow{v} v重合,那么能不能从 v → \overrightarrow{v} v下手,变换 v → \overrightarrow{v} v进而得到 x → \overrightarrow{x} x呢,回答是可以的。这里就用到了矩阵的逆,对 x → \overrightarrow{x} x的变换是正向变换,那么这个变换反向加到 v → \overrightarrow{v} v上就是逆向的变换,也就是逆矩阵 A − 1 A^{-1} A−1

我们定义一个逆向旋转
90
°
90 \degree
90°的变换,和它的逆向变换。
M
=
[
0
1
−
1
0
]
,
M
−
1
=
[
0
−
1
1
0
]
,
M = \left [ \begin{array}{c} 0 & 1\\ -1 & 0 \end{array} \right], M^{-1} = \left [ \begin{array}{c} 0 & -1\\ 1 & 0 \end{array} \right],
M=[0−110],M−1=[01−10],
M
M
M和
M
−
1
M^{-1}
M−1的乘积如下,结果显示变换
M
−
1
M
M^{-1}M
M−1M是一个什么都不做的变换。
M
−
1
M
=
[
1
0
0
1
]
M^{-1}M = \left [ \begin{array}{c} 1 & 0\\ 0 & 1 \end{array} \right]
M−1M=[1001]
利用这个特性,我们可以完成第一种情况下的求解。
A
−
1
A
x
→
=
A
−
1
v
→
x
→
=
A
−
1
v
→
A^{-1}A \overrightarrow{x} =A^{-1} \overrightarrow{v} \\ \overrightarrow{x} = A^{-1} \overrightarrow{v}
A−1Ax=A−1vx=A−1v
矩阵
A
A
A只要不将空间压缩为低维度的空间(
det
(
A
)
≠
0
\det(A) \neq 0
det(A)=0),就可以通过求
A
−
1
A^{-1}
A−1来求解方程。
det ( A ) = 0 \det(A) = 0 det(A)=0 / 列空间 / 零空间
当矩阵的行列式为0时,也就以为着矩阵将高维空间压缩到了低维空间,而这时我们是没有办法求解, A A A的逆操作的。以 A A A将二维空间压缩为一条线为例,它的逆操作就是将一条线“解压缩”为一个平面,这意味着将一个确定的线映射到无穷多个不确定的线,至少对于一个变换来讲是不可能的。
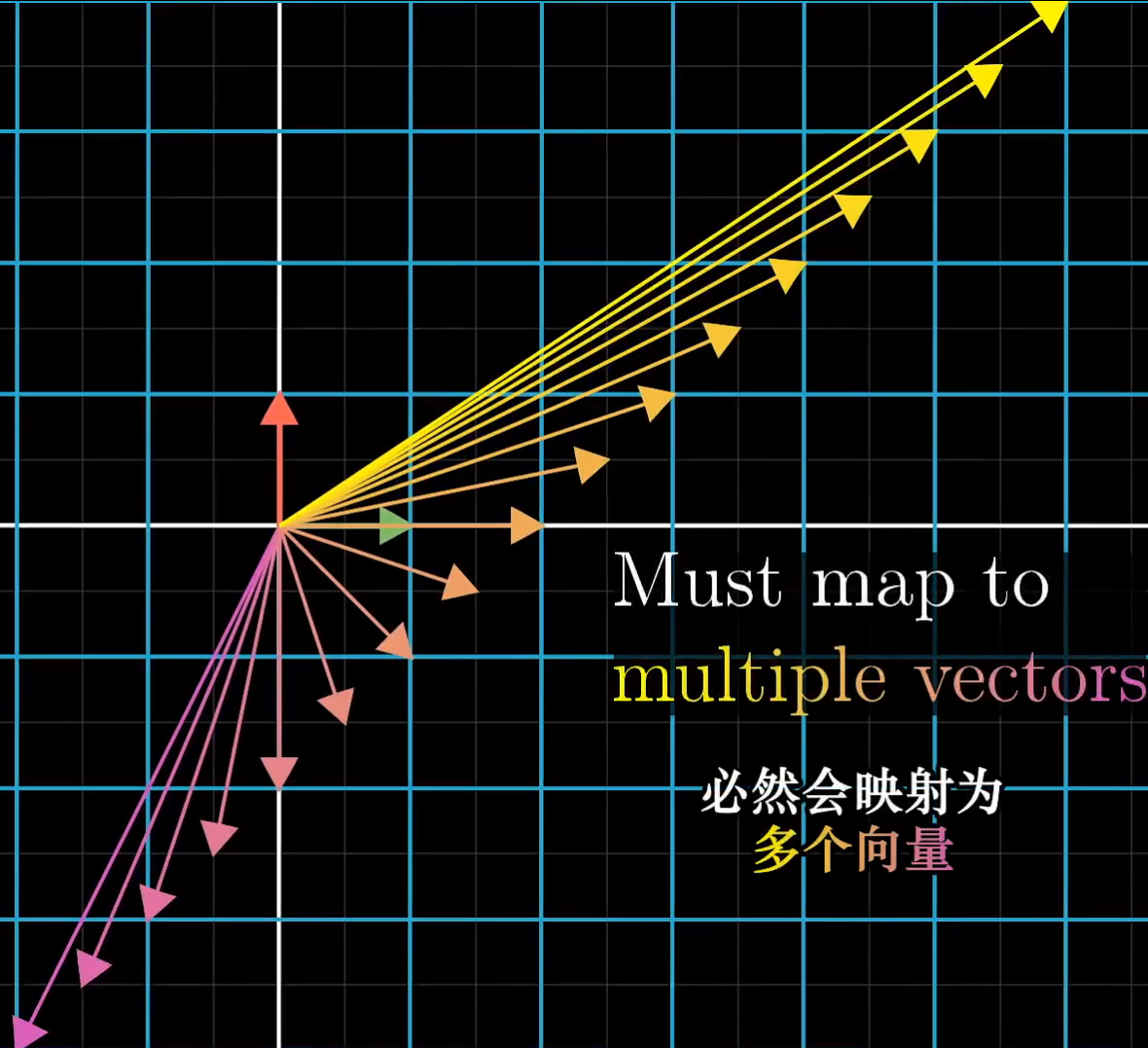
尽管这种情况下,逆操作是不可求的,但是仍然可能存在解。
秩
如果一个变换将高维空间压缩到了一维,那么我们说这个变换的秩是1,压缩到了平面,那么我们说这个变换的秩是2,以此类推。矩阵的秩,代表了矩阵对应的线性变换将空间变换后空间的维数。
 |  |
|---|
列空间
列空间就是矩阵的列所张成的空间。秩更精确的定义是列向量的维数。秩达到最大时,意味着秩与列数相等。
 |  |
|---|
零空间
变换后落在原点的向量的集合,被称为矩阵的零空间或者“核”。如下图,我们可以看到黄色线上的点被压缩到的原点。
 |  |  |  |
|---|
方程的解
回到求解方程中,零空间就是这个向量方程所有可能的解。
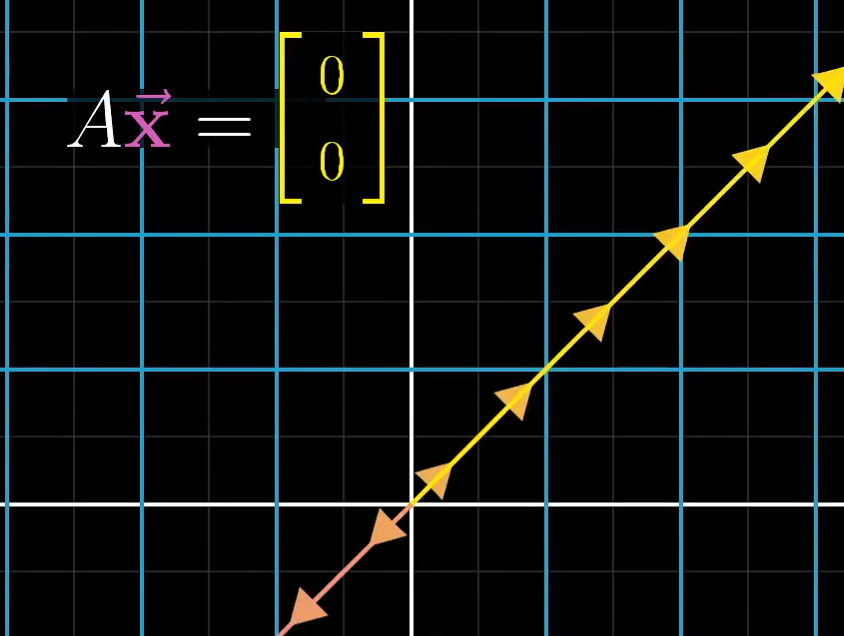
然后,我们可以看如下三个方程。他们分别等价于下面的二元一次方程。
[
1
1
1
1
]
[
x
y
]
=
[
0
0
]
,
[
1
1
1
1
]
[
x
y
]
=
[
1
1
]
,
[
1
1
1
1
]
[
x
y
]
=
[
1
2
]
\left[ \begin{array}{c} 1 & 1 \\ 1 & 1\\ \end{array}\right]\left[ \begin{array}{c} x \\ y \\ \end{array}\right] = \left[ \begin{array}{c} 0 \\ 0\\ \end{array}\right], \left[ \begin{array}{c} 1 & 1 \\ 1 & 1\\ \end{array}\right]\left[ \begin{array}{c} x \\ y \\ \end{array}\right] = \left[ \begin{array}{c} 1 \\ 1 \\ \end{array}\right], \left[ \begin{array}{c} 1 & 1 \\ 1 & 1\\ \end{array}\right]\left[ \begin{array}{c} x \\ y \\ \end{array}\right] = \left[ \begin{array}{c} 1 \\ 2 \\ \end{array}\right]
[1111][xy]=[00],[1111][xy]=[11],[1111][xy]=[12]
{ x + y = 0 x + y = 0 , { x + y = 1 x + y = 1 , { x + y = 1 x + y = 2 \begin{cases} x+y=0\\ x+y=0\\ \end{cases}, \begin{cases} x+y=1\\ x+y=1\\ \end{cases}, \begin{cases} x+y=1\\ x+y=2\\ \end{cases} {x+y=0x+y=0,{x+y=1x+y=1,{x+y=1x+y=2
显然,前两个方程有无穷多个解,分别是直线 x + y = 0 x+y=0 x+y=0和 x + y = 1 x+y=1 x+y=1。第三个方程中两个式子是矛盾的, x + y x+y x+y不可能即等于1,又等于2。
现在,以线性变换的角度观察这个矩阵
M
M
M。
M
=
[
1
1
1
1
]
M = \left [ \begin{array}{c} 1 & 1 \\ 1 & 1\\ \end{array} \right ]
M=[1111]
M
M
M所代表的线性变换将二维空间压缩到了
y
=
x
y=x
y=x这条直线上。那么求解第一个方程时,就是找到哪些点被变换到了原点,在二维空间中还是能很容易联想出来这个答案的,那必然是垂直于
y
=
x
y=x
y=x这条直线的的一条直线。
[
1
1
1
1
]
[
x
y
]
=
[
0
0
]
\left[ \begin{array}{c} 1 & 1 \\ 1 & 1\\ \end{array}\right]\left[ \begin{array}{c} x \\ y \\ \end{array}\right] = \left[ \begin{array}{c} 0 \\ 0\\ \end{array}\right]
[1111][xy]=[00]
结合下面的图可以更为直观看出
M
M
M这个变换将二维空间沿着与
x
x
x轴
135
°
135 \degree
135°方向压缩成一条直线。
那么对于如下方程,我们也可以在向量空间中进行求解,即
M
M
M变换作用于空间后,被压缩到
[
1
1
]
T
[1 \,\, 1]^T
[11]T位置的向量集合就是这个方程的解。
[
1
1
1
1
]
[
x
y
]
=
[
1
1
]
\left[ \begin{array}{c} 1 & 1 \\ 1 & 1\\ \end{array}\right]\left[ \begin{array}{c} x \\ y \\ \end{array}\right] = \left[ \begin{array}{c} 1 \\ 1 \\ \end{array}\right]
[1111][xy]=[11]
最后对于最后一个方程组而言,二维空间被压缩到
x
=
y
x=y
x=y这条直线上,这个一维空间中不可能有向量是
[
1
2
]
T
[1 \,\, 2]^T
[12]T
[
1
1
1
1
]
[
x
y
]
=
[
1
2
]
\left[ \begin{array}{c} 1 & 1 \\ 1 & 1\\ \end{array}\right]\left[ \begin{array}{c} x \\ y \\ \end{array}\right] = \left[ \begin{array}{c} 1 \\ 2 \\ \end{array}\right]
[1111][xy]=[12]
参考内容
强烈推荐观看3Blue1Brown,我的评价是醍醐灌顶。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








