2021-05-05

基于MATLAB仿真的杨氏双缝干涉

1.双缝干涉的原理

• 首先上杨氏双缝干涉的原理图`，在关注几个必要的参数。（d：两缝间距；D：缝到屏的距离；θ：倾角很小旁轴近似（D>>d，tanθ≈sinθ）；设光程差为δ）

• P点的光强I§为两光相干叠加的结果，相干叠加公式如下：

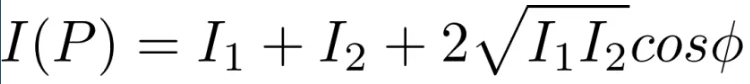
​ 设位相为φ，则φ=2πδ/λ。先假设光源是单色光源，且S、S1、S2都很小可视为点孔，且S1、S2分居在以S为中轴线两侧，则由相干叠加知观察屏上的光强分布为其中，φ为相位=2πδ/λ，I1为经过S1后的光强，I2为经过S2后的光强（设I1=I2），则可以将I§化为

• 计算相位差，对于光程差δ，δ=L1-L2,设观察屏上P点坐标为x，在傍轴区（D>>d)，可将L1+L2≈2D，即可得δ=L1-L2=xd/D，则由几何关系得：

---

2.MATLAB代码

close all;
clear;
%第一部分输入必要的参数
lambda=input('输入光的波长（单位nm）：');
lambda=lambda*1e-9;%将nm换算到m
d=input('输入两个缝的间距（单位mm）：');
d=d*0.001;%将mm换算到m
D=input('输入缝到屏的距离（单位m）：');


%第二部分输入必要的参数
xMax=5*lambda*D/d;%xMax为观察屏上的最大视野,取其为5倍△x
N=1001;%N表示步数
x=linspace(-xMax,xMax,N);%x表示观察屏上P点坐标，



%第三部用相干叠加求相干光强
for i=1:N

    L1=sqrt((x(i)-d/2).^2+D^2);%L1为S1点孔发出的光至观察屏的光程

    L2=sqrt((x(i)+d/2).^2+D^2);%L2为S2点孔发出的光至观察屏的光程

    Phi=2*pi*(L2-L1)/lambda;%phi即φ，φ=2π·δ/λ为相位差，δ=L2-L1为光程差

    I(i,:)=4*cos(Phi/2).^2;%I表示光强分布，I(i,:)表示矩阵I第i行所有元素

end


%第四部将光强分布转化为灰度图

graylevel=255;%灰度等级为255

Ir=(I/4.0)*graylevel;%将光强I先归一化，再“归255化”

subplot(1,2,1),image(xMax,x,Ir);

colormap(gray(graylevel)),title('条纹图')%colormap(map) 用map矩阵映射当前图形的色图

subplot(1,2,2),plot(I(:),x),title('光强分布')

---

3.结果展示

输入的各个参数：

输出的结果：

结论：

1.干涉明条纹的位置可由干涉极大条件d=kλ得：x=(L/d)kλ,干涉暗条纹位置可由干涉极小条件d=(k+1/2)λ得：x=(D/d)(k+1/2)λ。

2.明条纹之间、暗条纹之间距都是Δx =λ(D/d)，干涉条纹是等距离分布的。

3.而且注意上面的公式都有波长参数在里面，波长越长，相差越大。

4.条纹形状：为一组与狭缝平行、等间隔的直线（干涉条纹特点）菲涅尔双棱镜，菲涅尔双面镜、埃洛镜的干涉情况都与此类似。

---

---

后记、、、若改为复色光干涉结果如下

clear;

lambda=input('输入光的中心波长（单位nm）：');

lambda=lambda*1e-9;%将nm换算到m

d=input('输入两个缝的间距（单位mm）：');

d=d*0.001;%将mm换算到m

D=input('输入缝到屏的距离（单位m）：');

xMax=5*lambda*D/d;%xMax为观察屏上的最大视野,取其为5倍△x

N=1000;%N表示个数

x=linspace(-xMax,xMax,N);%x表示观察屏上P点坐标，

%用相干叠加求相干光强

for i=1:N

    L1=sqrt((x(i)-d/2).^2+D^2);%L1为S1点孔发出的光至观察屏的光程

    L2=sqrt((x(i)+d/2).^2+D^2);%L2为S2点孔发出的光至观察屏的光程

    %Phi=2*pi*(L2-L1)/lambda;%phi即φ，φ=2π·δ/λ为相位差，δ=L2-L1为光程差

    %I(i,:)=4*cos(Phi/2).^2;%I表示光强分布，I(i,:)表示矩阵I第i行所有元素

    n=10;dlamda=linspace(-0.1,0.1,n);%dlamda为波长宽度范围

    Lambda=lambda*(1+dlamda');%得到一系列波长

    Phi=2*pi*(L2-L1)./Lambda;%得到一系列相位

    I(i,:)=sum(4*cos(Phi/2).^2)/n;%sum表示不同频率光强非相干叠加，并归一化

end

%将光强分布转化为灰度图

graylevel=255;%灰度等级为255

Ir=(I/4.0)*graylevel;%将光强I先归一化，再“归255化”

subplot(1,2,1),image(xMax,x,Ir);

colormap(gray(graylevel)),title('条纹图')

%colormap(map) 用map矩阵映射当前图形的色图

subplot(1,2,2),plot(I(:),x),title('光强分布')

输入的参数：

得到的结果：

---

白光产生彩色的干涉条纹

结论：随条纹极次绝对值升高，不同频率的单色波在观察屏上趋向于你来我往的相互填平，而不再像零级条纹那样步调一致地相长相消，导致干涉效应逐渐减弱，条纹衬比度显著下降。仿真结果与实验结果一致。
（引用b站光电面壁人，https://www.bilibili.com/read/cv9217066，本人小白学习中）