第二章 数据结构 堆

1、算法思路

如何手写一个堆？

需求：

1. 建堆
2. 可以插入一个数
3. 可以求堆中的最小（最大）值
4. 可以删除最小值
5. 删除任意一个元素
6. 修改任意一个元素

下面以小根堆为例

1.堆的基本性质

1. 堆是一个完全二叉树
2. 分为大根堆和小根堆。大根堆是指每个节点都大于其左右子节点，小根堆是指每个节点都小于其左右子节点。
3. 小根堆的根节点是最小值，大根堆的根节点存储最大值

2. 堆的存储

对于所有的完全二叉树，都可以使用一个一维数组进行存储。

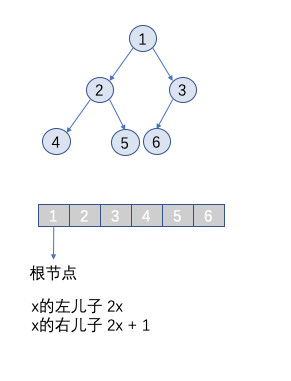
根据上图的关系，就可以把一个完全二叉树用一维数组进行存储。注意这里根节点从1开始计算,从0开始也可以实现，但是不太方便。

3. 两个基本操作 down\up

down和up一个是向下调整，一个是向上调整。使用这两个操作就可以实现上述需求。
下面是down操作的示意图。

同理up操作的示意图如下：

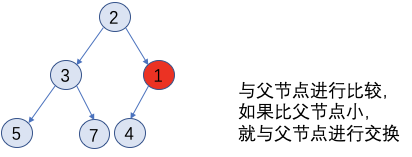
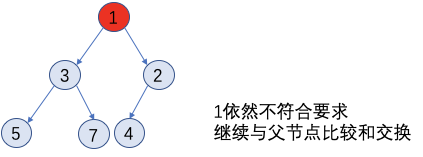
4. 利用上述操作完成需求

我们定义一维数组heap，其长度为size

1. 建堆(将一个普通数组变成堆）

//假设元素一开始散乱的存在heap数组里
for(int i = size / 2; i; i --)
{
	down(i);
}

第size / 2个元素，是完全二叉树中，第一个非叶子节点。
如下图所示

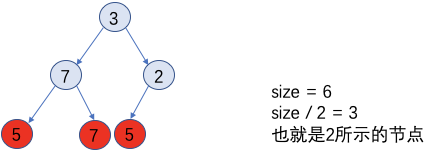
首先我们假设最后一排红颜色的叶节点已经是堆了，那么从第一个非叶子节点开始向下调整，先调整2所在的子树，再调整7所在的子树，调整后如下图所示

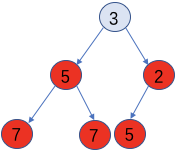
此时红颜色的两个子树已经是堆了，再从根节点（也就是i=1的时候）进行down操作。

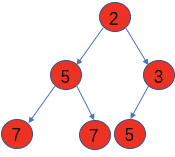
一个小根堆就建好了，干净又卫生。

2. 插入一个数x

//在尾部插入一个数，并执行up操作
heap[++ size] = x;
up(size)

3. 求堆中的最小（最大）值

heap[1]

4. 删除最小(最大)值

//也就是删除第一个元素
//我们将堆中最后一个元素放到第一个位置上，并将最后一个元素删除,并执行down操作
//因为删除最后一个数字比较简单，只需要size --即可
heap[1] = heap[size]; size --; down(1);

5. 删除第k个（任意一个）元素

//与删除第一个元素是类似的
//只是最后我们既执行了down操作，又执行了up操作，
//因为我们不知道k和最后一个size位置上的数字哪一个大，都写上但只有一个会执行。
heap[k] = heap[size]; size --; down(k);up(k);

6. 修改（第k个）任意一个元素

heap[k] = x; down(k);up(k);

2、模板代码

这里主要写一下down和up两个操作的代码

1. down操作

假设存储堆的一维数组为h,长度为size

void down(int u)
{
	int t = u; 
	if(u * 2 <= size && h[u * 2] < h[t]) t  = u * 2;
	if(u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
	if (u != t)
    {
        swap(h[u], h[t]);
        down(t);
    }
}

2. up操作

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        swap(h[u], h[u / 2]);
        u >>= 1;
    }
}

3、时间复杂度分析

1. 建堆操作时间复杂度分析

推广到一般情况，就是
第一层 $n/2$个元素不需要调整
第二层 $n/4$个元素需要调整一次
…
所以时间复杂度
$$S=n/2\ast 0+n/4\ast 1+n/8\ast 2+...=n(1/2^2+2/2^3+...)$$$$2S=n(1/2+2/2^2+....)$$$$2S-S=n(1/2+1/2^2+1/2^3+...)$$
后面这个级数是小于1的，所以建堆的时间复杂度是$O(n)$的

2、up和down操作

up和down操作跟堆的高度有关，时间复杂度为$O(logn)$

参考资料

Acwing