图的最短路径(迪杰斯特拉和弗洛伊德）算法

最短路径问题

文章目录：

• 最短路径的概念
• 迪杰斯特拉算法
• 弗洛伊德算法

1.最短路径

    首先我们要清楚什么是最短路径，怎么样称为最短。
    概念：从图中的某个顶点出发到达另外一个顶点的所经过的边的权重（权值）之和最小的一条路径，称为最短路径。

知道了什么是最短路径之后，怎么样实现这个最短路径问题，找到给出某个图中的最短路径呢，下面介绍两种实现最短路径的算法（迪杰斯特拉和弗洛伊德）这里注意一点：
通常采用迪杰斯特拉算法求图中某一顶点到其余各顶点的最短路径
通常采用弗洛伊德算法求图中任意一对顶点间的最短路径
下面首先来讲解迪杰斯特拉算法

2.迪杰斯特拉算法

1.算法思想：

设有两个顶点集合S和T，集合S中存放图中已找到最短路径的顶点，集合T存放图中剩余顶点，初始状态时，集合S中只包含顶点V0，然后不断从集合T中选取到顶点v0路径长度最短的顶点Vu并入到集合S中。这里需要注意的是，集合S每并入一个新的顶点Vu，都要修改顶点V0到集合T中顶点的最短路径长度值。之后不断重复此过程，直到集合T的顶点全部并入到S中为止。
这里详细说一下为什么要每并入新的顶点都要修改顶点V0到集合T中顶点的最短路径长度值
在Vu被选入S中后，Vu被确定为最短路径上的顶点，此时Vu就像V0到达T中顶点的中转站，多了一个中转站，就会多一些到达T中顶点的新的路径，而这些新的路径有可能比之前V0到T中顶点的路径要短，因此如果比之前路径短的话需要修改原有V0到T中其他顶点的路径长度。

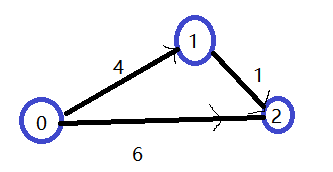
如图所示，首先刚开始1并入S中，并入后多了1—2的路径，原来0—2的路径长度为6，而现在通过1这个“中转站”，使得0—2的路径变为4+1=5小于原来0–2的路径长度6，所以就要修改之前0—2路径的长度。

相信你已经了解了很多，下面给出算法的执行过程：
2.图解执行过程

引进三个辅助数组：dist[],path[]和set[]。

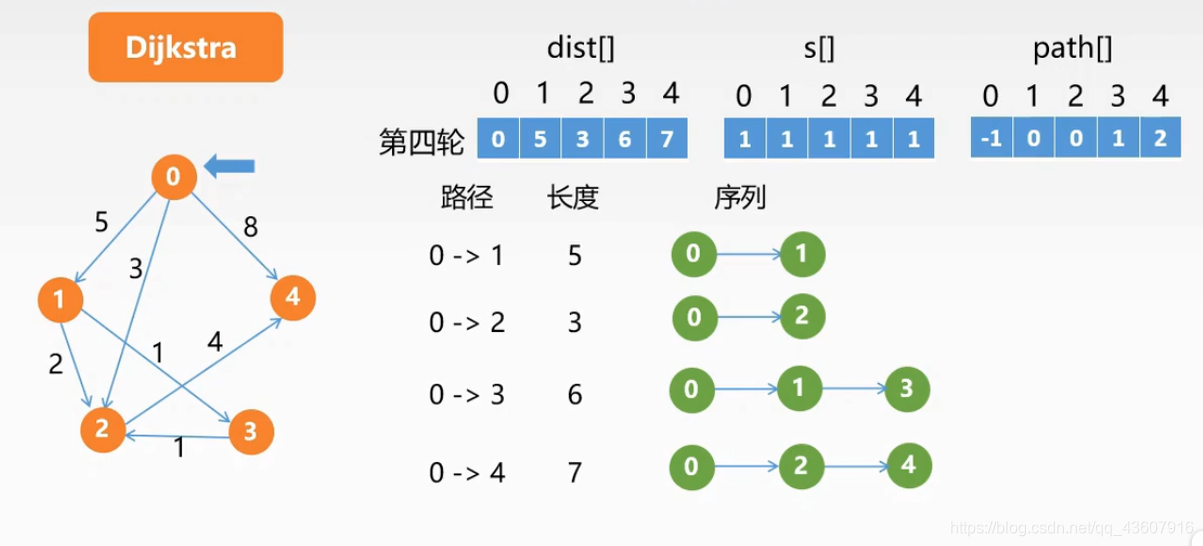
• dist[Vi]表示当前已找到的从V0到每个终点Vi的最短路径长度，它的初态为：若从V0到Vi有边，则dist[Vi]为边上的权值，否则置dist[Vi]为∞。
• path[Vi]中保存从V0到Vi最短路径上Vi的前一个顶点假设最短路径上的顶点序列为V0，V1，V2…Vi-1,Vi,则path[Vi]=Vi-1;path[]的初态为：如果V0到Vi有边，则path[Vi]=V0,否则path[Vi]=-1。
• set[]为标记数组，set[Vi]=0表示Vi在T中，即没