支持向量机(SVM)最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出,目前的版本(soft margin)是由 Corinna Cortes 和 Vapnik 在1993年提出。在深度学习(2012)出现之前,SVM 被认为机器学习中近十几年来最成功,表现最好的算法。
SVM 基本概念
将实例的特征向量(以二维为例)映射为空间中的一些点,它们属于不同的两类。给定训练样本集
D
=
(
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
m
,
y
m
)
)
,
y
i
∈
{
−
1
,
1
}
D=((x_1,y_1),(x_2,y_2),...,(x_m,y_m)),yi∈\{−1,1\}
D=((x1,y1),(x2,y2),...,(xm,ym)),yi∈{−1,1}, (假设样本线性可分),线性分类器基于训练样本D在二维空间中找到一个超平面来分开二类样本。

但是符合条件的线是有无数条可以画的,区别就在于效果好不好。SVM 的目的就是想要画出一条线,以“最好地”区分这两类点,以至如果以后有了新的点,这条线也能做出很好的分类。

挑选的标准:
SVM 将会寻找可以区分两个类别并且能使边际(margin)最大的超平面,这个超平面离直线两边的数据的间隔最大,对训练集的数据的局限性或噪声有最大的“容忍”能力。
边际(margin)就是某一条线距离它两侧最近的点的距离之和,下图中两条虚线构成的带状区域就是 margin,虚线是由距离中央实线最近的两个点所确定出来的。第一种划分方式 margin 比较小,如果用第二种方式画,margin 明显变大也更接近我们的目标。

构造超平面
超平面可以用函数
f
(
X
)
=
W
T
X
+
b
f(X)=W^TX+b
f(X)=WTX+b 表示。 当
f
(
X
)
f(X)
f(X)等于0的时候,
X
X
X便是位于超平面上的点,而
f
(
X
)
f(X)
f(X)大于0的点对应
y
=
1
y=1
y=1的数据点,
f
(
X
)
f(X)
f(X)小于0的点对应
y
=
−
1
y=-1
y=−1的点。
y
y
y只是一个label ,标注为
{
−
1
,
+
1
}
\{-1,+1\}
{−1,+1}不过为了描述方便,使得分类正确的情况下
y
i
(
W
T
x
i
+
b
)
>
=
1
y_i(W^Tx_i+b)>=1
yi(WTxi+b)>=1 。
- W:权重向量, w = { w 1 , w 2 , . . . , w n } , n w=\{w_1,w_2,...,w_n\},n w={w1,w2,...,wn},n是特征值的个数
- X:训练实例
- b:bias 偏向
假定我们找到了这个超平面,以二维特征向量举例,即
X
=
(
x
1
,
x
2
)
X=(x_1,x_2)
X=(x1,x2),然后定义一下离这个线最近的点到这个分界面(线)的距离分别为d1,d2。
我们认为最佳分界面不偏向与任何一方,分界面到两边的举例相等,即d1=d2。
再假设我们有这两个平行于分界面的虚线,分别过离分界面最近的样本点。
假设分界面离上下虚线是k个距离,即虚线方程为
∣
W
T
X
+
b
∣
=
k
|W^TX+b|=k
∣WTX+b∣=k,两边同除k并不会改变这条线,因此可以通过调整权值使上下虚线的方程变为
∣
W
T
X
+
b
∣
=
1
|W^TX+b|=1
∣WTX+b∣=1。

我们的目的是使虚线之间的距离D最大,首先计算上虚线与分界面的距离:
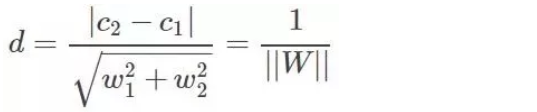
下虚线与分界面的距离也为d,因此:
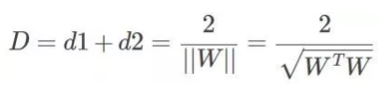
要想寻找距离D的最大值,则等价于求
∣
∣
W
∣
∣
||W||
∣∣W∣∣的最小值,也等同于求
∣
∣
W
∣
∣
2
||W||^2
∣∣W∣∣2即
W
T
W
W^TW
WTW的最小值,为了后续计算方便,我们再加一个系数1/2。因此可以构建一个目标函数:

但这个结论是有前提的,即所有的样本点在虚线上或虚线外,即
y
i
(
W
T
x
i
+
b
)
>
=
1
y_i(W^Tx_i+b)>=1
yi(WTxi+b)>=1 。
因此,完整的目标函数为:
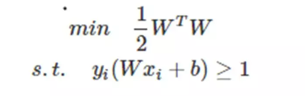
s
.
t
.
s.t.
s.t.表示受约束于,此时每个样本点都受此约束,假设有N个样本,代表该目标函数的约束条件有N个。
接下来只要找到在约束条件下使目标函数最小的 W W W,带入方程求出 b b b,便找到了最佳分界面。
拉格朗日乘子法
我们已经构造出了目标函数,但在众多约束条件下求解有些困难,这里我们需要引入拉格朗日乘子法。
等式约束
解决一个组合优化问题,一般需要拉格朗日乘子法,这里举个例子:
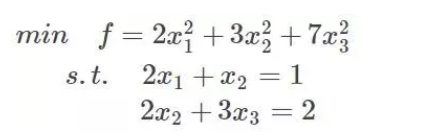
如果没有约束条件,我们可以对
f
f
f求导,最值一定位于极值点处。但有约束条件的情况下,极值点可能不满足约束条件。
既然有了约束不能直接求导,那么可以思考如何把约束去掉。既然是等式约束,那么我们把这个约束乘一个系数加到目标函数中去,这样就相当于既考虑了原目标函数,也考虑了约束条件,比如上面那个函数,加进去就变为:
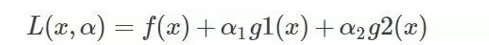
这里
g
1
(
x
)
,
g
2
(
x
)
g1(x),g2(x)
g1(x),g2(x)为约束函数,
α
1
,
α
2
\alpha_1,\alpha_2
α1,α2为系数。
分别求
L
L
L对
x
,
α
x,\alpha
x,α的偏导,令其为0,求
L
L
L的极值,因为
α
\alpha
α的偏导就是约束函数,令其为零就代表此时的
L
L
L等于
f
f
f,且满足约束条件。
上例中:

两个变量(
α
1
,
α
2
\alpha_1,\alpha_2
α1,α2)两个等式(约束条件),可以求解,最终可以得到系数
α
1
,
α
2
\alpha_1,\alpha_2
α1,α2,再带回去求x就可以了。
不等式约束——KKT条件
带有不等式的约束问题怎么办?那么就需要用更一般化的拉格朗日乘子法,即KKT条件,来解决这种问题了。
任何原始问题约束条件无非最多3种,等式约束,大于号约束,小于号约束,而这三种最终通过将约束方程化简化为两类:约束方程等于0和约束方程小于0。再举个简单的方程为例,假设原始约束条件为下列所示:
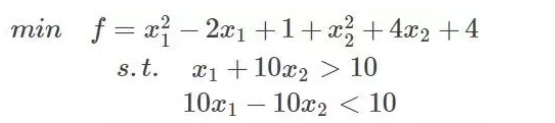
那么把约束条件变个样子:

把约束条件变成小于是为了后续计算方便。
将约束拿到目标函数中去就变成:
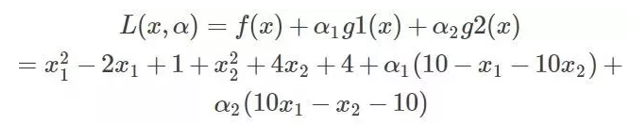
KKT条件的定理:
如果一个优化问题在转变完后变成

其中g是不等式约束,h是等式约束。那么KKT条件就是函数的最优值,它必定满足下面条件
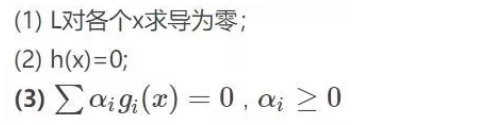
此时分别对x1、x2求导数:

(1)α1=α2=0,那么看上面的关系可以得到x1=1,x2=−1,再把两个x带到不等式约束,发现第一个就是需要满足(10-1+20=29<0)显然不行,29>0的,舍弃。
(2)g1(x)=g2(x)=0,带进去解得,x1=110/101;x2=90/101,再带回去求解α1,α2α1,α2,发现α1=58/101,α2=4/101,它们满足大于0的条件,那么显然这组解是可以的。
SVM目标函数求解
我们刚才构造了SVM的目标函数:
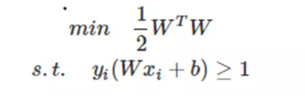
把约束条件换成小于号的形式:
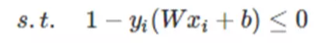
引入拉格朗日乘子法了,优化的目标变为:

注意,
W
T
W
W^TW
WTW为凸函数,因此才能使用KKT。由于
α
i
>
=
0
\alpha_i>=0
αi>=0,
h
i
(
x
)
<
=
0
h_i(x)<=0
hi(x)<=0,所以
L
(
w
,
b
,
α
)
L(w,b,\alpha)
L(w,b,α)一定小于等于原目标函数,则求原目标函数最小值的问题便成了求在KKT条件下
L
(
w
,
b
,
α
)
L(w,b,\alpha)
L(w,b,α)的最大值。
求导:
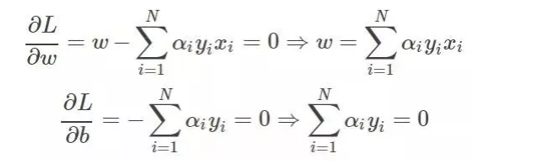
带入原式:

最终的问题为:
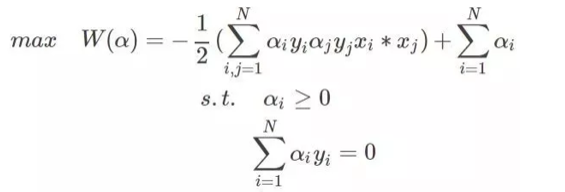
至此,可以用SMO法解出最优解
α
i
∗
\alpha_i^*
αi∗,进而求出
W
∗
W^*
W∗与
b
∗
b^*
b∗。
SMO法下文详细介绍,接下来先讨论线性不可分的情况。
线性不可分的情况
上述所有的构造都是在数据完全线性可分的情况下,且分界面完全将两类分开,若正负两类的最远点没有明显的分解面,甚至存在一些离群点或者噪声点而线性不可分,导致整个系统用不了。

SVM考虑到这种情况,所以在上下分界面上加入松弛变量
ξ
i
\xi_i
ξi,认为如果正类中有点到上界面的距离小于
ξ
i
\xi_i
ξi,那么认为他是正常的点,哪怕它在上界面稍微偏下一点的位置,同理下界面。

这样,约束条件就变成了:
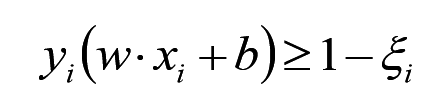
目标函数:

拉格朗日函数:
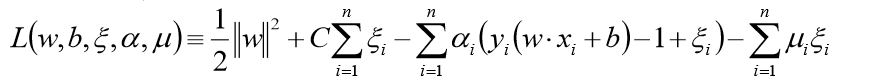
最终的问题为:

接下来和线性可分的情况一样,用SMO法解出最优解
α
i
∗
\alpha_i^*
αi∗,进而求出
W
∗
W^*
W∗与
b
∗
b^*
b∗。
SMO算法
SVM问题最终演化为求下列带约束条件的问题:

问题的解就是找到一组
α
i
∗
\alpha_i^*
αi∗使得
W
W
W最小。
每次只选择其中两个乘子做优化,其他因子认为是常数。将N个解问题,转换成两个变量的求解问题:并且目标函数是凸的。
考察目标函数,假设
α
1
\alpha_1
α1和
α
2
\alpha_2
α2是变量,其余均为定值:

SMO迭代公式:

退出条件:

核函数
可以使用核函数,将原始输入空间映射到新"的特征空间,从而使得原本线性不可分的羊本可能在核空间可分。
常用的核函数:
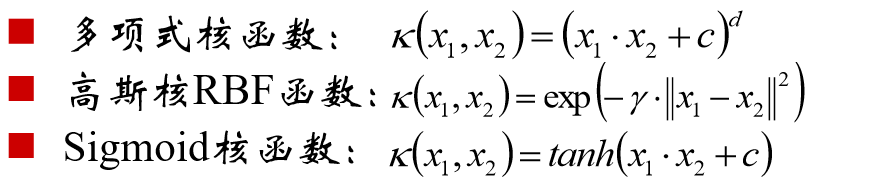
使用核函数的意义在于:
- 将向量的维度从低维映射到高维
- 降低运算复杂度降低运算复杂度






















 2265
2265











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








