坐标系相关
uv可能会影响局部坐标系,如果light图和brdf图做卷积的时候,局部坐标系保持一致很重要
如下图:tangent是从外部模型文件进行加载的

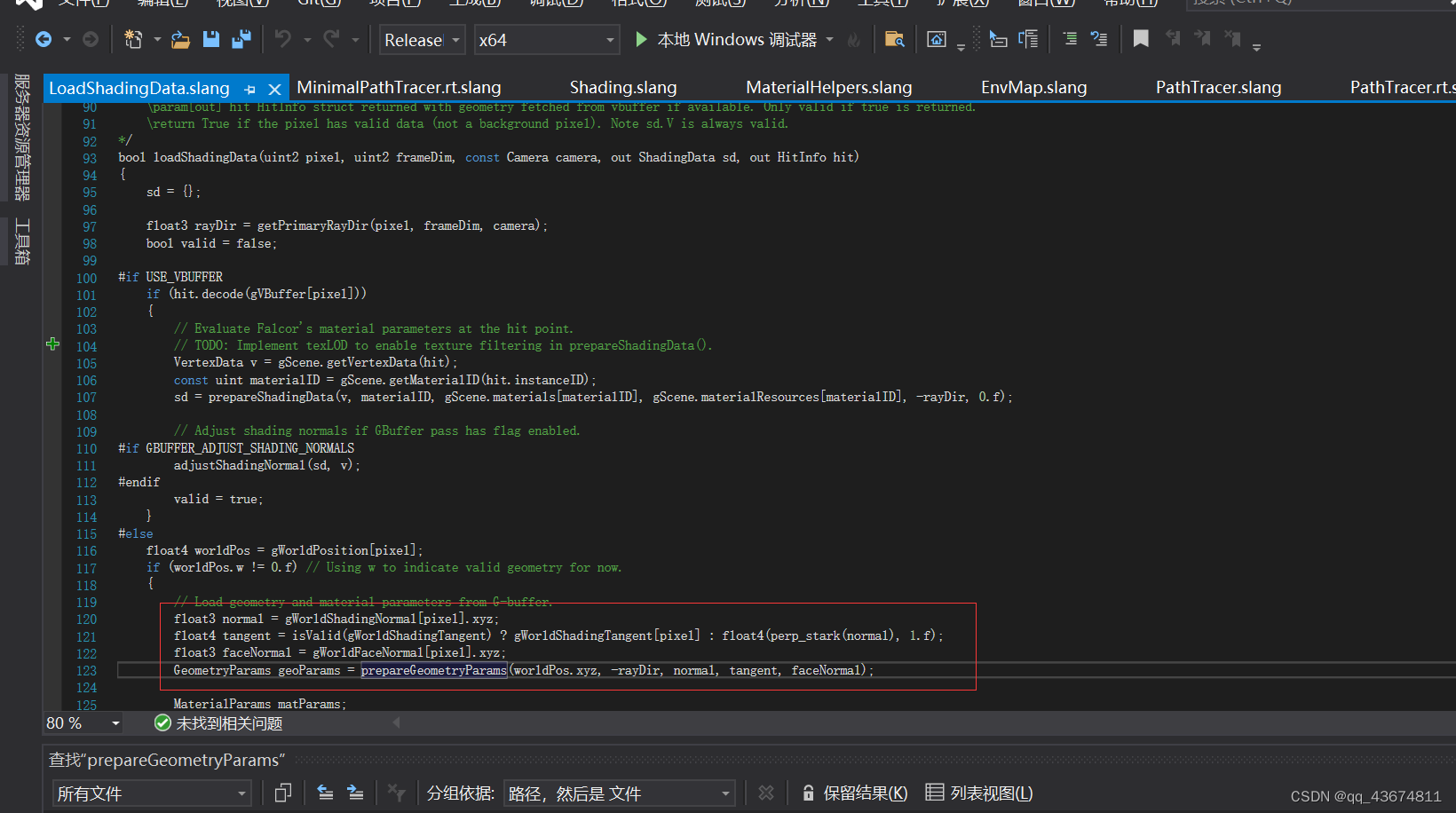
切线空间采样并转世界坐标系
// spherical to cartesian (in tangent space)
vec3 tangentSample = vec3(sin(theta) * cos(phi), sin(theta) * sin(phi), cos(theta));
// tangent space to world
vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N;
其中theta、phi是切线空间极坐标系,是随机采样出来的;然后转为直角坐标系,这里不需要考虑直角坐标系x,y,z的顺序,但在从切线空间转世界空间时,cos(theta)要和 N 对应上。
对于up right可以这样生成,它们怎么样生成都可以,只要和N向量构成两两垂直即可,但如果up向量和N向量相同的话,做cross可能会有一定风险(cross出来是0向量):
vec3 up = vec3(0.0, 1.0, 0.0);
vec3 right = normalize(cross(up, N));
up = normalize(cross(N, right));
Games101作业转换坐标系是这么做的:
里面的B,C向量相当于up,right,主要学习里面C向量的设计,这样设计可以使得C向量不会为0向量且一定垂直于N。
//切线直接坐标的a向量转换到世界空间
Vector3f toWorld(const Vector3f &a, const Vector3f &N){
Vector3f B, C;
//这里的条件判断,应该是为了避免出现C向量为0向量的情况
if (std::fabs(N.x) > std::fabs(N.y)){//至少在x轴上有分量
float invLen = 1.0f / std::sqrt(N.x * N.x + N.z * N.z);
//C和N点乘为0,相互垂直;C向量不为0
C = Vector3f(N.z * invLen, 0.0f, -N.x *invLen);
}
else {//至少在y或z方向上有分量
float invLen = 1.0f / std::sqrt(N.y * N.y + N.z * N.z);
C = Vector3f(0.0f, N.z * invLen, -N.y *invLen);
}
B = crossProduct(C, N);
return a.x * B + a.y * C + a.z * N;
}
...
在ssao中有对up和right做扰动来增加采样的随机性,其中生成了扰动向量randomVec,然后做施密特正交化过程,使得randomVec垂直于N。
vec3 randomVec = texture(texNoise, TexCoords * noiseScale).xyz;
vec3 tangent = normalize(randomVec - normal * dot(randomVec, normal));//施密特正交化过程,使得tangent必与normal垂直
vec3 bitangent = cross(normal, tangent);
mat3 TBN = mat3(tangent, bitangent, normal);
assimp中的tangent与bitangent
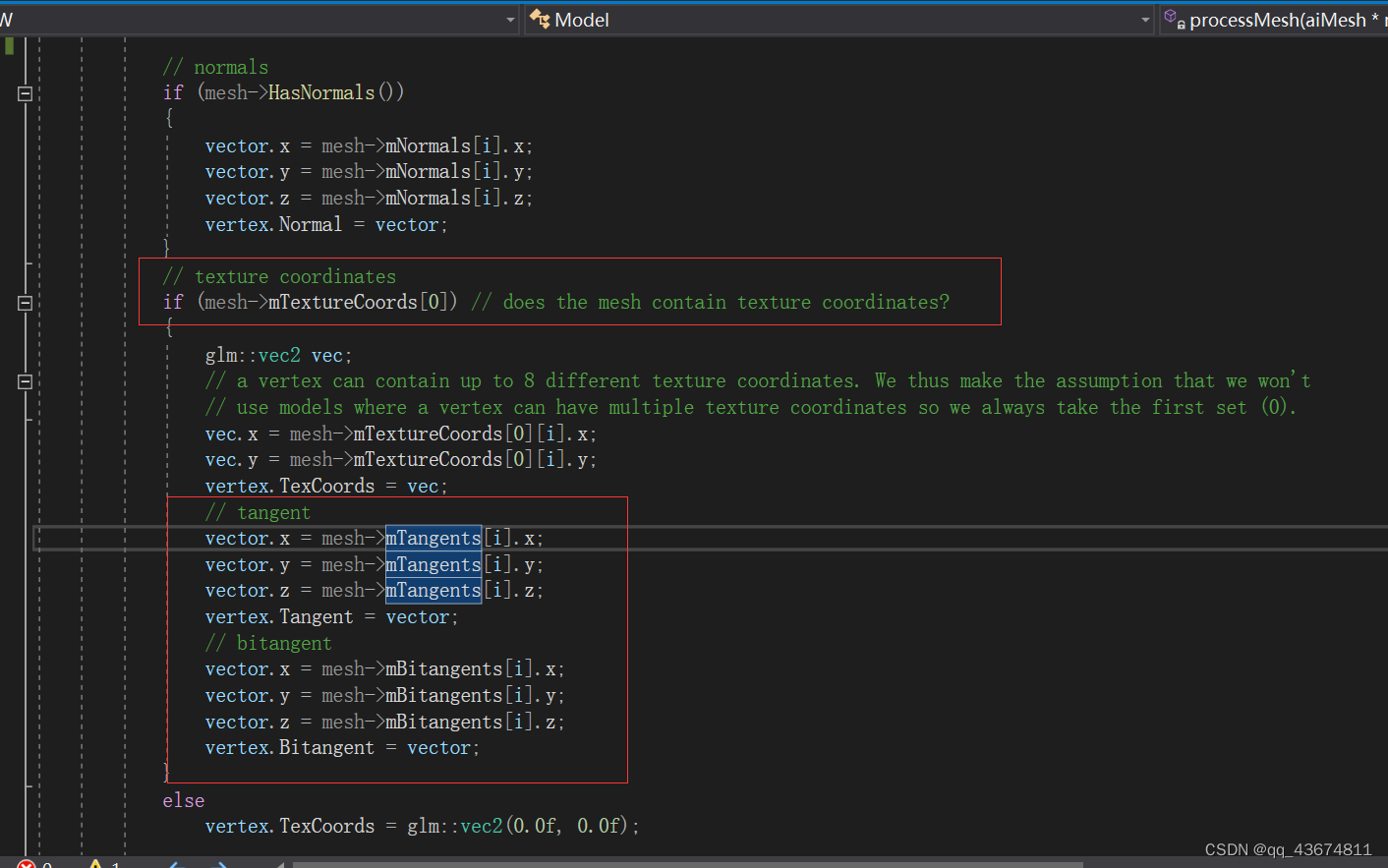
有texcoord一般也默认带上了tangent和bitangent
Falcor中获取垂直向量
// Utility function to get a vector perpendicular to an input vector
// (from "Efficient Construction of Perpendicular Vectors Without Branching")
float3 getPerpendicularVector(float3 u)
{
float3 a = abs(u);
uint xm = ((a.x - a.y)<0 && (a.x - a.z)<0) ? 1 : 0;
uint ym = (a.y - a.z)<0 ? (1 ^ xm) : 0;
uint zm = 1 ^ (xm | ym);
return cross(u, float3(xm, ym, zm));
}
后续 Falcor半球cosine采样以及均匀采样 有用到
随机数
CPU
inline float get_random_float()
{
std::random_device dev;
std::mt19937 rng(dev());
std::uniform_real_distribution<float> dist(0.f, 1.f);
return dist(rng);
}
GPU
1.低差异序列

设总样本数为 N,样本索引为 i
// ----------------------------------------------------------------------------
// http://holger.dammertz.org/stuff/notes_HammersleyOnHemisphere.html
// efficient VanDerCorpus calculation.
float RadicalInverse_VdC(uint bits)
{
bits = (bits << 16u) | (bits >> 16u);
bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}
用法:
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
Falcor中使用的random(GPU)
- 在raygen中根据FrameCount和pixelId去initRand
// Generates a seed for a random number generator from 2 inputs plus a backoff
uint initRand(uint val0, uint val1, uint backoff = 16)
{
uint v0 = val0, v1 = val1, s0 = 0;
[unroll]
for (uint n = 0; n < backoff; n++)
{
s0 += 0x9e3779b9;
v0 += ((v1 << 4) + 0xa341316c) ^ (v1 + s0) ^ ((v1 >> 5) + 0xc8013ea4);
v1 += ((v0 << 4) + 0xad90777d) ^ (v0 + s0) ^ ((v0 >> 5) + 0x7e95761e);
}
return v0;
}
使用如下:
// Initialize a random seed, per-pixel, based on a screen position and temporally varying count
uint randSeed = initRand(launchIndex.x + launchIndex.y * launchDim.x, gFrameCount, 16);
- 假设需要在cosHemiSphere上进行采样
for (int i = 0; i < gNumRays; i++)
{
// Sample cosine-weighted hemisphere around surface normal to pick a random ray direction
float3 worldDir = getCosHemisphereSample(randSeed, worldNorm.xyz);
// Shoot our ambient occlusion ray and update the value we'll output with the result
// 因为不是 蒙特卡洛,因此这里的cos采样 不需要考虑 概率
ambientOcclusion += shootAmbientOcclusionRay(worldPos.xyz, worldDir, gMinT, gAORadius);
}
getCosHemisphereSample函数定义,注其返回的是世界坐标系下的vector:
// Get a cosine-weighted random vector centered around a specified normal direction.
float3 getCosHemisphereSample(inout uint randSeed, float3 hitNorm)
{
// Get 2 random numbers to select our sample with
float2 randVal = float2(nextRand(randSeed), nextRand(randSeed));
// Cosine weighted hemisphere sample from RNG
float3 bitangent = getPerpendicularVector(hitNorm);
float3 tangent = cross(bitangent, hitNorm);
float r = sqrt(randVal.x);
float phi = 2.0f * 3.14159265f * randVal.y;
// Get our cosine-weighted hemisphere lobe sample direction
return tangent * (r * cos(phi).x) + bitangent * (r * sin(phi)) + hitNorm.xyz * sqrt(1 - randVal.x);
}
其中nextRand定义如下:其返回的是一个[0…1]的随机数,同时也更新随机数种子
// Takes our seed, updates it, and returns a pseudorandom float in [0..1]
float nextRand(inout uint s)
{
s = (1664525u * s + 1013904223u);
return float(s & 0x00FFFFFF) / float(0x01000000);
}
采样
半球内均匀采样(CPU)
Vector3f Material::sample(const Vector3f &wi, const Vector3f &N){
switch(m_type){
case DIFFUSE:
{
// uniform sample on the hemisphere
float x_1 = get_random_float(), x_2 = get_random_float();
float z = std::fabs(1.0f - 2.0f * x_1);
float r = std::sqrt(1.0f - z * z), phi = 2 * M_PI * x_2;
Vector3f localRay(r*std::cos(phi), r*std::sin(phi), z);
return toWorld(localRay, N);
break;
}
}
}
GGX重要性采样(GPU)
参考:https://blog.csdn.net/weixin_43803133/article/details/110385305


vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)//输入Xi随机数以及法线N,在tangent space的半球上随机获取一个向量,并返回到世界坐标系
{
float a = roughness*roughness;
float phi = 2.0 * PI * Xi.x;
float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
float sinTheta = sqrt(1.0 - cosTheta*cosTheta);
// from spherical coordinates to cartesian coordinates - halfway vector
vec3 H;
H.x = cos(phi) * sinTheta;
H.y = sin(phi) * sinTheta;
H.z = cosTheta;
// from tangent-space H vector to world-space sample vector
vec3 up = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
vec3 tangent = normalize(cross(up, N));
vec3 bitangent = cross(N, tangent);
vec3 sampleVec = bitangent * H.x + tangent * H.y + N * H.z;
return normalize(sampleVec);
}
使用如下:用于生成镜面朝向。
for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
// generates a sample vector that's biased towards the preferred alignment direction (importance sampling).
vec2 Xi = Hammersley(i, SAMPLE_COUNT);
vec3 H = ImportanceSampleGGX(Xi, N, roughness);
...
Falcor半球cosine采样以及均匀采样
注意这些都返回的是世界坐标系下的vector:
cosine 采样:
// Get a cosine-weighted random vector centered around a specified normal direction.
float3 getCosHemisphereSample(inout uint randSeed, float3 hitNorm)
{
// Get 2 random numbers to select our sample with
float2 randVal = float2(nextRand(randSeed), nextRand(randSeed));
// Cosine weighted hemisphere sample from RNG
float3 bitangent = getPerpendicularVector(hitNorm);
float3 tangent = cross(bitangent, hitNorm);
float r = sqrt(randVal.x);
float phi = 2.0f * 3.14159265f * randVal.y;
// Get our cosine-weighted hemisphere lobe sample direction
return tangent * (r * cos(phi).x) + bitangent * (r * sin(phi)) + hitNorm.xyz * sqrt(1 - randVal.x);
}
对应的概率:NdotL / M_PI
均匀采样:
// Get a uniform weighted random vector centered around a specified normal direction.
float3 getUniformHemisphereSample(inout uint randSeed, float3 hitNorm)
{
// Get 2 random numbers to select our sample with
float2 randVal = float2(nextRand(randSeed), nextRand(randSeed));
// Cosine weighted hemisphere sample from RNG
float3 bitangent = getPerpendicularVector(hitNorm);
float3 tangent = cross(bitangent, hitNorm);
float r = sqrt(max(0.0f,1.0f - randVal.x*randVal.x));
float phi = 2.0f * 3.14159265f * randVal.y;
// Get our cosine-weighted hemisphere lobe sample direction
return tangent * (r * cos(phi).x) + bitangent * (r * sin(phi)) + hitNorm.xyz * randVal.x;
}
对应的概率:1.0f / (2.0f * M_PI)
使用如下:
if (gCosSampling)
bounceDir = getCosHemisphereSample(randSeed, worldNorm.xyz); // Use cosine sampling
else
bounceDir = getUniformHemisphereSample(randSeed, worldNorm.xyz); // Use uniform random samples

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








