python实现线性回归

最新推荐文章于 2024-05-04 13:29:01 发布

我超爱Debug

最新推荐文章于 2024-05-04 13:29:01 发布

阅读量3.8k

点赞数 2

分类专栏： python-信息分析与预测文章标签： python 可视化

本文链接：https://blog.csdn.net/qq_43741419/article/details/117075742

版权

python-信息分析与预测专栏收录该内容

5 篇文章 0 订阅

订阅专栏

文章目录

一、实验目的：
二、实验平台：
三、实验内容与结果：

一、实验目的：

实现一元(或多元)线性回归:

根据对客观现象的定性认识初步判断现象之间的相关性(略)
绘制散点图
进行回归分析，拟合出回归模型
对回归模型进行检验一计算相关系数、异方差检验(μ2- x图)
进行回归预测

实现离差形式的一元线性回归(可选)

二、实验平台：

Python 3.7

三、实验内容与结果：

3.1 题目分析

在这里插入图片描述
附上一些公式:
一元线性回归的最小二乘法的a和b求法:

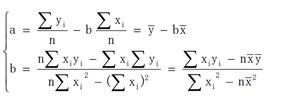
总方差，剩余方差，估计值方差公式:

相关系数的公式:

离差形式的最小二乘法的a和b的公式:

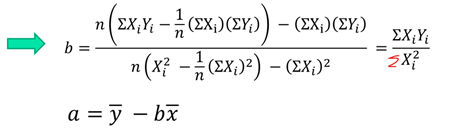
3.2 代码

# -*- codeing =utf-8 -*-
# @Time : 2021/5/8 21:36
# @Author : ArLin
# @File : demo1.py
# @Software: PyCharm
import csv
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']#正常显示汉字
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
#读取csv文件
def ReadCsvFile(path):
    File = open(path, 'r')
    f = csv.reader(File)
    i = 0
    data = []
    year=[]
    for row in f:
        if i > 0:#去头处理
            #data.append(row[1])
            #year.append(row[0])
           data.append(float(row[1]))
           year.append(float(row[0]))
        i = i + 1
    #print(year)
    #print(data)
    #安全性
    safe=1
    if len(year)==0:
        safe=0
    if len(data)==0:
        safe=0
    if len(year)!=len(data):
        safe=0
    if safe==0:
        print("读取的文件非有效数据，请检查文件")
        sys.exit(1)
    return year,data

#绘制散点图
def draw1(year,data):
    ryear=[]
    rdata=[]
    for index in range(len(year)):
        ryear.append(year[index])
        #rdata.append(data[index])
        rdata.append(data[index]/10000)
    plt.figure(1)
    #plt.title("1949-2019中国年末总人口(万人)")
    plt.title("1949-2019中国年末总人口(亿人)")
    plt.plot(ryear, rdata, '.')
    plt.xlabel('时间(年)')
    #plt.ylabel('年末总人口(万人)')
    plt.ylabel('年末总人口(亿人)')
    plt.show()
    return ryear,rdata


#拟合回归模型，进行回归预测
#离差方式的最小二乘法
def UnivariateLinearity(ryear,rdata):
    XiYi=0
    Ax=0
    Ay=0
    X2i=0
    for index in range(len(ryear)):
        XiYi=XiYi+ryear[index]*rdata[index]
        Ax=Ax+ryear[index]
        Ay=Ay+rdata[index]
        X2i=X2i+ryear[index]**2
    Ax=Ax/len(ryear)
    Ay=Ay/len(rdata)

    b=np.round((XiYi-len(ryear)*Ax*Ay)/(X2i-len(ryear)*Ax*Ax),3)
    t1=XiYi-len(ryear)*Ax*Ay
    t2=X2i-len(ryear)*Ax*Ax
    a=np.round(Ay-b*Ax, 3)

    print("回归模型为:y=",a,'+',b,"*x")
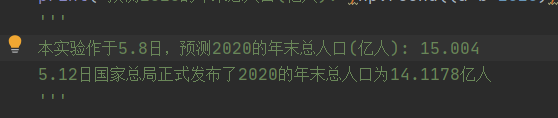
    print('预测2020的年末总人口(亿人):',np.round((a+b*2020),4))
    '''
    预测2020的年末总人口(亿人): 15.004
    本实验作于5.8号，5.12国家总局正式发布了2020的年末总人口为14.1178亿人
    '''
    #离差形式最小二乘法
    bb=np.round((XiYi/X2i),3)
    aa=np.round((Ay-bb*Ax),3)
    print("------离差形式最小二乘法分界线------")
    print("离差形式最小二乘法回归模型为:y=", aa, '+', bb, "*x")
    print('离差形式最小二乘法预测2020的年末总人口(亿人):', np.round((aa + bb * 2020), 4))
    print("------离差形式最小二乘法分界线------")





    #画出该回归模型的曲线(进行回归预测)
    newY=[]
    newYY=[]
    Ayy=[]
    for index in range(len(ryear)):
        newY.append( np.round(a+b*ryear[index],3))
        newYY.append(np.round(aa+bb*ryear[index],3))#离差形式
        Ayy.append(Ay)
    plt.figure(2)
    plt.title("1949-2019中国年末总人口(亿人)")
    plt.plot(ryear, rdata, '.',label="真实数据")
    plt.plot(ryear, newY, 'r',label="回归模型曲线")
    plt.plot(ryear, newYY,':', label="离差形式回归模型曲线")
    plt.plot(ryear, Ayy, '--g', label="总人口平均值")
    plt.legend(["真实数据", "回归模型曲线","离差形式回归模型曲线","总人口平均值"])
    plt.xlabel('时间(年)')
    plt.ylabel('年末总人口(亿人)')
    plt.show()
    return newY,Ay,
'''
#对回归模型进行检验—计算相关系数、异方差检验
def examine(ryear,rdata,newdata,Ay):
    T_variance=0#总方差
    R_variance=0#剩余方差
    VE_value=0#估计值方差

    for index in range(len(ryear)):
        T_variance=T_variance+(rdata[index]-Ay)*(rdata[index]-Ay)
        R_variance=R_variance+(rdata[index]-newdata[index])**2
        VE_value=VE_value+(newdata[index]-Ay)**2
    T_variance= np.round(T_variance/len(ryear), 3)
    R_variance=np.round(R_variance/len(ryear), 3)
    VE_value=np.round(VE_value/len(ryear), 3)
    co_coefficient=(1-R_variance)**0.5
    print('总方差为:', T_variance, '剩余方差为:', R_variance, '估计值方差为', VE_value,'相关系数为:',co_coefficient)

'''
#对回归模型进行检验—计算相关系数、异方差检验(升级版可视化写法)
def examine(ryear,rdata,newdata,Ay):
    T_variancei=[]#总方差i
    R_variancei=[]#剩余方差i
    VE_valuei=[]#估计值方差i
    for index in range(len(ryear)):
        T_variancei.append((rdata[index]-Ay)**2)
        R_variancei.append((rdata[index]-newdata[index])**2)
        VE_valuei.append((newdata[index]-Ay)**2)
    T_variance= np.round(sum(T_variancei)/len(ryear), 3)
    R_variance=np.round(sum(R_variancei)/len(ryear), 3)
    VE_value=np.round(sum(VE_valuei)/len(ryear), 3)
    print('总方差为:', T_variance, '剩余方差为:', R_variance, '估计值方差为', VE_value)
    #安全性处理2
    if R_variance<=1:
        co_coefficient = np.round(((1 - R_variance) ** 0.5), 3)
        print('相关系数为',co_coefficient)
    '''
     #画图
    year2=[]
    year3=[]
    for i in ryear:
        year2.append(i + 0.1)
        year3.append(i + 0.2)

    plt.figure(3)
    plt.title("拟合优度检验")
    plt.bar(ryear, T_variancei, width=0.1, color='r', label="总方差")
    plt.bar(year2, R_variancei, width=0.1, color='g', label="剩余方差")
    plt.bar(year3, VE_valuei, width=0.1, color='b', label="估计值方差")
    plt.legend(["总方差", "剩余方差","估计值方差"])
    plt.xlabel('时间(年)')
    plt.ylabel('误差值(亿人)')
    plt.show()
    
    '''
    # 画图
    plt.figure(3)
    plt.title("拟合优度检验")
    plt.plot(ryear, T_variancei, '--g', label="总方差")
    plt.plot(ryear, R_variancei,':b', label="剩余方差")
    plt.plot(ryear, VE_valuei,'r', label="估计值方差")
    plt.legend(["总方差", "剩余方差", "估计值方差"])
    plt.xlabel('时间(年)')
    plt.ylabel('误差值(亿人)')
    plt.show()
    # 画图
    plt.figure(4)
    plt.title('μ^2- x散点图')
    plt.plot(ryear, R_variancei, '.r', label="方差")
    plt.xlabel('时间(年)')
    plt.ylabel('误差值(亿人)')
    plt.show()

if __name__ =='__main__':
    path = 'data.csv'
    #path='test1data.csv'
    data=ReadCsvFile(path)
    rdata=draw1(data[0],data[1])
    newdata=UnivariateLinearity(rdata[0], rdata[1])
    examine(rdata[0],rdata[1], newdata[0],newdata[1])

3.3结果与分析：

结果截图与实验结果分析:
1.绘制散点图:
在这里插入图片描述
利用所绘的散点图我们可以看出中国的年末总人口数和时间的分布呈现出一定的线性关系，我们可以进行回归分析

拟合回归模型，进行回归预测(包含离差形式的一元线性回归)

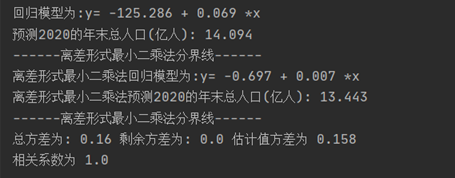
这个预测的结果和现实有亿点点的差距，我查看了国家统计局的报告以及结合图形我们可以看出我国人口年平均增长率为0.53%，与2000-2010年0.57%的人口年平均增长率相比，增速有所放缓。
但是线性回归方程默认的增长率为13.4%,离差形式的平均增长率为0.5%,
说明我国的人口增长虽然整体上从1949-2020年是一元线性趋势且增长率为13.4%，但是如果单单从2000-2020的数据量来说也是呈现一元线性趋势，但是增长率由13.4%下降到了6.9%,这个增长率的不同乘上了亿人这个单位后，就会显得误差非常大

在这里插入图片描述
3.对回归模型进行检验—计算相关系数、异方差检验

在这里插入图片描述

在总方差一定的前提下，剩余方差越大，则估计值方差越小。
剩余方差反映了原始数据点对回归直线的密切程度，剩余方差
越小，回归直线的代表性越高;剩余方差越大，原始数据点越
偏离回归直线，回归直线的拟合度越差。
从图中我们可以得知剩余方差为0.123较小，回归直线额代表性较高
相关系数R为0.936，说明中国的年末总人口数和年份为高度相关
在这里插入图片描述
由图中的散点分布形状我么可以得知，该回归模型中的随机误差项是复杂型

3.4实验总结

出现的问题与解决方法:

问题1:
在人口以万人作为基本单位时，计算的方差都过于大
在这里插入图片描述

解决方法:
大胆的猜测可能是因为数据单位的选择导致的，所以我令总人口的最小单位作为亿，

这时候数据就变得正常了
问题2:
拟合优度检验可视化图表的选择，刚开始我是选择使用柱状图的形式来表示，但是因为数据量很大，而且有三个方差数据，这就导致了可视化并不美观
在这里插入图片描述
解决方法:
这时候其实我们可以选择从这70个数据中隔间距抽取数据来表示或者是直接改成连线图的形式表示，我选择了使用连线图来明了的表示

问题3:
Pythonmatlab图表中显示汉字和负号异常
解决方法:
经过网上资料的查询，我发现添加如下两句代码即可正常显示

3.5 个人总结:

本次的实验难度不大，选择了合理的数据后进行数据的处理，可视化显示，方法和前几次的实验基本都是一致的。故知识点总结不再扩展。
而让我觉得可以改进的地方其实就在于，我预测的2020年的人口量和真实的数据相差其实是0-1以内，问题在于这个基本单位是亿，那我应该选择精度更适合的回归模型，那我应该选择什么模型呢。但是由于目前时间的有限，我也只能带着这份疑问继续前进

3.6 答辩后的一些感悟

跟老师一对一的进行了本次实验的交流后有了一些启发，
首先是检验安全性，我做的是直接进行提示和退出程序，老师说在实际的程序设计中，最好不要直接粗暴退出程序，可以如果是空缺点的话，取前后两个值的平均值，或者直接取平均值补上去。但是如果表里确实是空数据的话，确实好像退出程序是较为明智的选择。
(当然这和个人的代码风格也比较相关
最小二乘法对噪声点比较敏感，我一开始是把几个点设为0，结果影响不大，我就以为这个结论是错的，后来询问了老师后，老师说是，我的噪声点设置太小，应该是把它们设成几千这种夸张的数据，更能直观
这里想说一下为什么最小二乘法是对噪声点比较敏感，因为最小二乘法是吸收所有的点，没有对数据做一个基本的判断。
第三就是我的离差形式的最小二乘法的可视化显示是有问题的，我取的X值是减去平均值后的值。(由于我中午没午睡，有点点脑壳儿疼，不想深究了
人口的拟合模型其实以一元线性回归的结果虽然也是较为准确了，但是如果想精确的话，可以采用生长曲线和对数曲线的形式可能预测结果会更为准确

我超爱Debug

关注

2
点赞
踩
19

收藏

觉得还不错? 一键收藏
0
评论
python实现线性回归

文章目录一、实验目的：二、实验平台：三、实验内容与结果：3.1 题目分析3.2 代码3.3结果与分析：3.4实验总结3.5 个人总结:3.6 答辩后的一些感悟一、实验目的：实现一元(或多元)线性回归:根据对客观现象的定性认识初步判断现象之间的相关性(略)绘制散点图进行回归分析，拟合出回归模型对回归模型进行检验一计算相关系数、异方差检验(μ2- x图)进行回归预测实现离差形式的一元线性回归(可选)二、实验平台：Python 3.7三、实验内容与结果：3.1 题目分析附上
复制链接

扫一扫