面向P、NPC、NP-Hard问题的调研报告

NP-完全问题的求解复杂性决定NP=P是否成立。1970年，COOK证明了SAT∈NPC。此后，人们证明了3000个以上的问题的NP完全性。关于NP完全问题的求解复杂性有许多猜测和分析，很多人倾向于NP完全问题不是多项式时间可解的，即NP≠P。1987年，图论六大难题之一的子图同胚问题终获解决，更多的人开始倾向于NP=P。

1 引言

上世纪60年代中期，Hartmanis等人提出了按照对资源(时间、空间)需求的不同来划分问题的方法，开创了计算复杂性理论。此后几年，随着研究的深入，越来越多的问题涌现出来，而经典的P =?NP问题则是计算复杂性中的核心问题。2000年，美国克雷实验室将其收录为“千禧年大奖”七个问题之首。

Р和NP问题及其相关概念比较抽象而复杂。对Р和NP问题的研究，关键有两个方面，第一是对相关概念的正确理解和把握，第二是正确的研究方向与正确的研究方式方法。对于第一点，由于相关概念相当复杂抽象，存在着许多理解上的谬误，甚至一些翻译过来的教科书都存在这些谬误，从而影响了该专业的学生正确理解掌握相关概念。对于第二点，关键是倾向于以NP等于Р为出发点还是相反。不同的出发点，对研究的成功与否，起着至关重要的作用。

而在所有NP相关问题中，NP完全即NPC无疑是最重要的概念。事实上，对NP完全及其相关概念的透彻理解，是深入研究NP问题，尤其是研究NP与P的关系问题的关键。谈到NP完全，又不能不涉及到多项式归约。

本次调研目的是，通过分析与NP问题相关的核心概念，并通过对抽象定义的解析，揭示其实质。本此调研的关键点是，深入剖析P问题和NP完全问题时间复杂度的逻辑内涵，同时通过对多个实际问题的分析比对，给出解决NP完全问题的启发式思路。

2 调研基础

2.1 基础知识

1.多项式时间

多项式时间(Polynomial time)在计算复杂度理论中，指的是一个问题的计算时间{\displaystyle m(n)}不大于问题大小{\displaystyle n}的多项式倍数。任何抽象机器都拥有一复杂度类，此类包括可于此机器以多项式时间求解的问题。

2.时间复杂度

时间复杂度表示的是在解决一个问题时，随着问题规模的扩大，解决问题所需要的时间的增长情况。在计算机科学中，用时间复杂度来衡量算法的效率。如果不管数据规模有多大，程序处理花的时间始终是固定的，那么就说这个程序具有o(1)的时间复杂度，也称常数复杂度。如果数据规模变得有多大，程序处理花的时间也跟着变得有多长，那么这个程序的时间复杂度就是O(n)，也称线性复杂度。数据规模与花费的时间成对数关系，那么这个程序的时间复杂度就是o(logn)，也称对数复杂度。常见的还有O(n2)、o(n3)、o(nlogn)、o(an)(a为常数)、O(n!)。

时间复杂度排序O(1)<O(n)<O(nlogn)<O(n^2)<O(n^a)<O(e^n) <o(n!)；

多项式级别：O(1)<O(n)<O(nlogn)<O(n^2)<O(n^a)；

非多项式级别：O(e^n)<O(n!)，计算机难以承受。

3.确定性算法与非确定性算法

设A是求解问题B的一个解决算法，在算法的整个执行过程中，每一步都能得到一个确定的解，这样的算法就是确定性算法。

而非确定性算法设A是求解问题B的一个解决算法，它将问题分解成两部分，分别为猜测阶段和验证阶段，其中。

猜测阶段：在这个阶段，对问题的一个特定的输入实例x产生一个任意字符串y，在算法的每一次运行时，y的值可能不同，因此，猜测以一种非确定的形式工作。

验证阶段：在这个阶段，用一个确定性算法〈有限时间内）验证。①检查在猜测阶段产生的y是否是合适的形式，如果不是，则算法停下来并得到no；②如果y是合适的形式，则验证它是否是问题的解，如果是，则算法停下来并得到yes，否则算法停下来并得到no，它是验证所猜测的解的正确性。

4.规约/约化

问题A可以约化为问题B，称为“问题A可规约为问题B”，可以理解为问题B的解一定就是问题A的解，因此解决A不会难于解决B。由此可知问题B的时间复杂度一定大于等于问题A。一个问题规约为另一个问题，时间复杂度增加了，问题的应用范围也增大了。通过对某些问题的不断规约，我们能够不断寻找复杂度更高，但应用范围更广的算法来代替复杂度虽然低，但只能用于很小的一类问题的算法。存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。这种问题的存在难以置信，并且更加不可思议的是，这种问题不只一个，它有很多个，它是一类问题。这一类问题就是传说中的NPC问题，也就是NP-完全问题[2]。

2.2 相关概念

1.P问题

所有能用多项式时间算法计算得到结果的问题，称为多项式问题，也就是P问题。

2.NP问题

多项式复杂程度的非确定性问题，这些问题无法根据公式直接地计算出来，这是在多项式时间内“可验证”的问题。也就是说，不能判定这个问题到底有没有解，而是猜出一个解来在多项式时间内证明这个解是否正确。即该问题的猜测过程是不确定的，而对其某一个解的验证则能够在多项式时间内完成。P类问题属于NP问题，但NP类问题不一定属于P类问题。需要注意的是，NP问题不是非P类问题，强调：P和NP不是对立的概念，而是包含的概念。NP问题是指可以在多项式的时间里验证一个解的问题。NP问题的另一个定义是，可以在多项式的时间里猜出一个解的问题。

3.NPC问题

NPC问题(Non-deterministic Polynomial complete)：NP完全问题，可以这么认为，这种问题只有把解域里面的所有可能都穷举了之后才能得出答案，这样的问题是NP里面最难，但是这样算法的复杂程度，是指数关系。一般说来，如果要证明一个问题是NPC问题的话，可以拿已经是NPC问题的一个问题经过多项式时间的变化变成所需要证明的问题，那么所要证明的问题就是一个NPC问题了。NPC问题是一个问题族，如果里面任意一个问题有了多项式的解，即找到一个算法，那么所有的问题都可以有多项式的解。

4.NP-hard问题

NP-Hard问题：NP-hard满足所有的NP问题都可以用多项式时间约化到它，但并不要求其是一个NP的问题。或者说，NP-hard是所有问题的上届。也就是说，所有问题都不比NP-hard难。NP-hard问题的范围比NPC的范围更大。如果某个问题S是NP-hard，那么对于任意一个NP问题，我们都可以把这个NP问题在多项式时间之内转化为S，并且原问题的答案和转化后S的答案是相同的。也就是说只要我们解决了S，那么就解决了所有的NP问题。

5.四者关系图

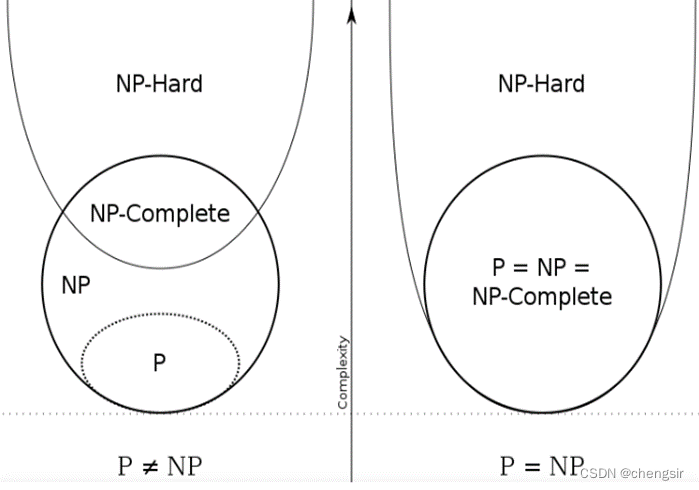
图1 P、NP、NPC、NPhard关系图

3 调研基本情况

3.1 P问题

在排序这个大问题里，是可以找到一种时间复杂度为多项式O(n2)，O(nlogn)的算法(如冒泡排序法，快速排序)来求解排序问题的，所以我们说排序问题是一个有多项式时间算法的问题。所以我们称，P类问题就是存在多项式时间算法的问题。

在计算机当中，排序问题是比较基础的，将输入按照大小或其他规则排好序，有利于后期运用数据进行其他运算。冒泡排序就是其中的一种排序算法。假设手上现在有n个无序的数，利用冒泡排序对其进行排序，

①首先比较第1个数和第2个数，如果后者>前者，就对调他们的位置，否则不变

②接着比较第2个数和第3个数，如果后者>前者，就对调他们的位置，否则不变

③一直向下比较直到第n-1和第n个数比较完，第一轮结束。（这时候最大的数移动到了第n个数的位置）

④重复前三步，但是只比较到第n-1个数（将第二大的数移动到第n-1个数位置）

⑤持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

举个实例：5,4,3,2,1，对其进行排序，先是比较5跟4变成4,5,3,2,1，第一轮结束后变成4,3,2,1,5，可以计算，当对其排序完正好要经过4+3+2+1=10次比较，当然这是最复杂的情况，即完全反序。可以知道对于n个数，至多要经过1+2+...+n-1即(n^2-n)/2次比较才能排好序。这个式子里n的最高次阶是2，可知道当n→∞时，一次性对其比较次数影响很小，所以我们把这个算法的时间复杂度比作：o(n^2)。取其最高次，可以看出，这是一个时间复杂度为多项式的表示方式。因为P类问题就是存在多项式时间算法的问题，所以冒泡排序就属于P问题[4]。

矩阵乘法是一个P类问题。对两个n阶方阵的乘积，即使采用求内积分别求积矩阵中各个元素的方法，其时间界也只有O(n3)，如果采用矩阵乘法的Stressen算法或凝聚算法,，则可以使时间界进一步降低[5]。

多项式求值问题是一个P类问题。若采用Horner算法对n次多项式求值，其时间界是n的线性函数。线性函数是一次多项式函数。

查找问题是一个P类问题。在n个有序的数集合{a1,a2,…,an}中查找一个数b，若采用二分查找算法，其时间复杂度仅为0(log2n)，这是比线性时间界还要低得多的一个复杂度，当然也是多项式时间界的。

属于P问题的问题，还有很多，算法时间复杂度如果满足多项式级别：O(1)<O(n)<O(nlogn)<O(n^2)<O(n^a)；那么此类问题属于P问题。

3.2 NPC问题

NPC类问题（Nondeterminism Polynomial complete）：存在这样一个NP问题，所有的‘NP’问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。其定义要满足2个条件：1）它得是一个NP问题；2）所有的NP问题都可以约化到它。即如果所有NP问题可在多项式时间内归约成某个NP问题，则该NP问题称为NP完全问题。也就是说NP完全问题既是NP-hard问题又是NP问题。

3.2 NP-Hard问题

指问题S，满足任何NP问题都可以在多项式级时间复杂度内被归约为S（归约：即被归约的NP问题与S的答案相同，当解决了S时，就同时解决了所有的NP问题）。可以理解为，这是一个比所有NP问题都难的问题。NP-hard问题： 假设存在这样一个问题，
1）任意np问题都可以在多项式时间内约化为该问题；
2）解决了该问题就解决了NP问题；这个问题就是NP-hard问题；
即 为了解决问题A，先将问题A约化为另一个问题B ， 解决问题B同时也间接解决了问题A。问题B就是一个NP-hard问题。

参考：

[1]杜立智,陈和平,符海东.NP完全问题研究及前景剖析[J].武汉工程大学学报,2015,37(10):73-78.

[2]网页https://blog.csdn.net/qq_29176963/article/details/8277654

[3]网页https://blog.csdn.net/databatman/article/details/4930429

[4]网页百度百科——全球领先的中文百科全书

[5]https://blog.csdn.net/u011046038/article/details/124727015