背包问题题解概述-CSDN博客

本文链接：https://blog.csdn.net/qq_43814415/article/details/140001240

来源于 https://kamacoder.com/problempage.php?pid=1046
也有一个很好的题解：
https://leetcode.cn/problems/last-stone-weight-ii/solutions/805162/yi-pian-wen-zhang-chi-tou-bei-bao-wen-ti-5lfv/

使用动态规划，五步走

1.定义状态数组和具体状态含义：

dp是个二维数组，第一维代表物品索引，第二维代表背包空间状态。
dp[i][j]是指物品i 在背包空间j 的情况下所能放的最大价值。

2.明确状态转移公式

根据题意，要么我放物品i ，要么不放。由易到难：

先考虑不放，那一定是我背包空间不够这个物品的体积才不放。所以此时dp[i][j] 的状态转移就是继承在背包空间j 的时候，物品i-1 （也就是上一个物品）时刻的状态： dp[i][j] = dp[i-1][j]

再考虑放，放的话首先要加上物品i 的价值，然后继承上一个能和物品i 的体积适配（也就是背包空间j去掉物品i 的体积后所剩的背包空间，在这个背包空间j-weigths[i-1]下的前一个物品i-1所得到的最大价值）的状态： dp[i][j] = dp[i-1][j-weigths[i-1]] + values[i-1]
这里为什么不是继承前一个物品在空间j下的状态，因为这样很可能两个物品加起来背包塞不下，为了尝试在物品i 时能成功塞到空间j 里，必须继承背包空间j-weigths[i-1]时的状态。

综合下，能够放的情况下，我也可以不放，这样就省了空间，有可能在后面有更有价值的。
所以考虑放的情况下也是放与不放取最大值。

问：为什么明明是物品i，空间j，但是每次都是weigths[i-1]、values[i-1]？
答：这与dp初始化有关，我在初始化时考虑了物品0和空间0，都代表不存在。但是weigths是列表，访问物品1的时候索引是0，物品0是不存在的。

问：什么是背包空间不够这个物品的体积？
答：如果空间j < weights[i-1]，说明物品i 的体积超过了当前空间。

3.初始化边界条件

根据定义，物品i为0时，代表没有物品，所以dp[0][j]=0
空间j为0时，代表没有空间，放不进去，所以dp[i][j]=0

4.遍历方式确定

按照先遍历一维，再遍历二维的方式。先遍历每个物品，再遍历每个背包空间。

5.举例推导dp

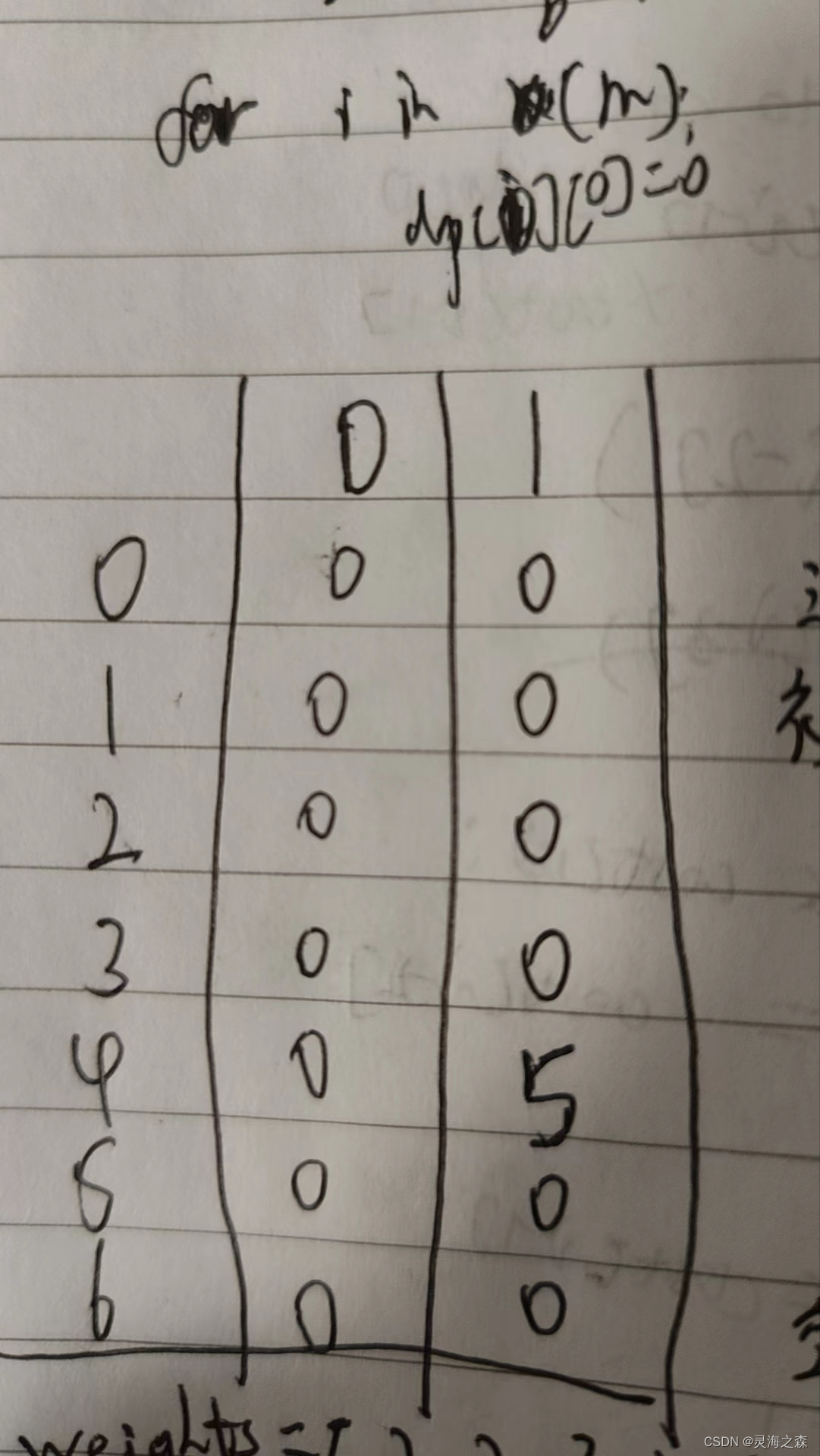
在这里插入图片描述

代码

ACM模式


import sys

# 从标准输入读取数据
input = sys.stdin.read
data = input().split()

# 解析第一个整数m（研究材料的种类）和第二个整数n（小明的行李空间）
m, n = int(data[0]), int(data[1])

# 解析研究材料所占空间的列表weights和研究材料价值的列表values
weights = list(map(int, data[2:2 + m]))
values = list(map(int, data[2 + m:2 + 2 * m]))

# 动态规划
# 状态数组dp，dp[i][j]表示前i个物品放入容量为j的背包中可以获得的最大价值
dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]

# 填充状态数组dp
for i in range(1, m + 1):  # 遍历每一个物品
    for j in range(1, n + 1):  # 遍历背包容量从1到n
        if weights[i - 1] > j:  # 如果当前物品的重量大于当前背包容量
            dp[i][j] = dp[i - 1][j]  # 当前物品不能放入背包，继承上一个状态
        else:
            # 当前物品可以放入背包，选择放入或不放入，取最大值
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1])

# 输出dp数组中dp[m][n]的值，即前m个物品放入容量为n的背包中可以获得的最大价值
print(dp[m][n])