写在前面:卡特兰数这东西感觉挺常用的,并且公式很简单,那就花一下午总结一下,学点皮毛吧(反正遇到我还是不会 )
文章目录
卡特兰数定义

卡特兰数的性质

记住前几项:
C
0
C_0
C0 =1,
C
1
C_1
C1 = 1,
C
2
C_2
C2 = 2,
C
3
C_3
C3 = 5,
C
4
C_4
C4 = 14
卡特兰数问题一般都存在匹配关系
(1)求组合数形式
C
n
=
(
2
n
n
)
n
+
1
=
(
2
n
n
)
−
(
2
n
n
−
1
)
C_n = \frac{\binom{2n}{n}}{n + 1} =\binom{2n}{n} - \binom{2n}{n-1}
Cn=n+1(n2n)=(n2n)−(n−12n)
求组合数有四种方法,详见:常用算法代码模版4—数学知识
(2)递推形式(这个递推公式用上面组合数形式推导一下就出来了!)
C
n
=
4
n
−
2
n
+
1
C
n
−
1
,
其中
C
0
=
C
1
=
1
C_n = \frac{4n-2}{n + 1}C_{n-1},\text{其中}C_0 = C_1 = 1
Cn=n+14n−2Cn−1,其中C0=C1=1
可以用递归来求,也可以用记忆化数组来求(空间换时间)
数据较大要取模 p 时,注意除数取模要先取逆元
(3)基本公式
C
n
+
1
=
∑
i
=
0
n
C
i
C
n
−
i
,
其中
C
0
=
C
1
=
1
C_{n+1} = \sum _ {i = 0} ^ n C_i C _ {n - i},\text{其中}C_0 = C_1 = 1
Cn+1=i=0∑nCiCn−i,其中C0=C1=1
或者
f
n
=
f
0
∗
f
n
−
1
+
f
1
∗
f
n
−
2
+
⋯
+
f
n
−
1
∗
f
0
,
其
中
n
>
=
2
f_n = f_0 * f_{n-1} + f_1 * f_{n - 2} + \cdots + f_{n-1}*f_0,其中n >= 2
fn=f0∗fn−1+f1∗fn−2+⋯+fn−1∗f0,其中n>=2
例如:1到n构成的二叉树搜索树的总数为 C n C_n Cn,则当以1为根节点时,左子树有0个节点,右子树有n-1个节点,所以有 C 0 ∗ C n − 1 C_0 * C_{n-1} C0∗Cn−1种,以2为根节点有 C 1 ∗ C n − 2 C_1 * C_{n-2} C1∗Cn−2种,所以 C n C_n Cn是卡特兰数,所以 C n = 4 n − 2 n + 1 C n − 1 , 其中 C 0 = C 1 = 1 C_n = \frac{4n-2}{n + 1}C_{n-1},\text{其中}C_0 = C_1 = 1 Cn=n+14n−2Cn−1,其中C0=C1=1
可以用二重循环求
说明:通常满足上面任意公式的都是卡特兰数
注意:由于卡特兰数增长速度较快,当 n 等于 17 时,卡特兰数将会超过 int 最大值,造成溢出(Python 除外),建议用long long来存。对于 Java 语言来说,可以使用 BigInteger 来计算大整数。

—— 摘自Wikipedia
卡特兰数证明(折线法)(n和m相同)
卡特兰数
C
n
=
(
2
n
n
)
n
+
1
=
C
(
2
n
,
n
)
n
+
1
=
(
2
n
n
)
−
(
2
n
n
−
1
)
C_n = \frac{\binom{2n}{n}}{n + 1} = \frac{C(2n,n)}{n + 1} =\binom{2n}{n} - \binom{2n}{n-1}
Cn=n+1(n2n)=n+1C(2n,n)=(n2n)−(n−12n)

LeetCode 96. 不同的二叉搜索树
LeetCode 题解 | 96. 不同的二叉搜索树(卡特兰数 C++)
n + 1 个叶子节点能够构成多少种形状不同的“xxx”二叉树
“xxx”二叉树的每个非叶子结点一定都有左右子树(匹配关系)
使用深度优先搜索这个二叉树,向左扩展时标记为 +1,向右扩展时标记为 -1
一个卡特兰序列(n + 1个点)对应一棵二叉树

例:买票
绘画展览门票每张5元,如果有2n个人排队购票,每人一张,并且其中一半人恰有5元钱,另一半人恰有10元钱,而票房无零钱可找,那么如何将这2n个人排成一列,顺次购票,使得不至于因票房无零钱可找而耽误时间,应该采用什么算法解决呢?
例:图书馆借还书
在图书馆一共6个人在排队,3个还《面试宝典》一书,3个在借《面试宝典》一书,图书馆此时没有了面试宝典了,求他们排队的总数?
解:队伍是排成一列的,联想Catalan证明的图
h ( 3 ) = 6 ! / ( 3 ! ∗ 4 ! ) = 5 h(3)=6!/(3!*4!)=5 h(3)=6!/(3!∗4!)=5,所以 总数 = h ( 3 ) ∗ 3 ! ∗ 3 ! = 180 \text{总数}=h(3)*3!*3!=180 总数=h(3)∗3!∗3!=180
注意:算种类时,最后要乘以3!和3!
例:出栈顺序
一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
思路
将问题转化为:入栈的数的个数总是要大于或者等于出栈数的个数。进栈相当于+1,出栈相当于-1
如:序列1 2 3的出栈序列可以表示为+1,-1,+1,+1,-1,-1

计算出栈序列数目,就是卡特兰数C(2n,n)/(n+1) (n=1,2,3,…)
例:括号匹配
n 对括号,则有多少种 “括号匹配” 的括号序列?
思路
左括号看成 +1,右括号看成 -1,类似进出栈
例:2*n矩阵(每行递增,每列递增)

思路
把第一排看作进栈+1,第二排看作出栈-1,同时要一直保证第一排填充的数大于等于第二排填充的数(递增要求)
按照 1 到 2n 的顺序填入矩阵,
1
1
1 放第一排,对应卡特兰序列中
x
1
=
+
1
x_1=+1
x1=+1,…
显然:长度为2n的卡特兰序列与2 X n矩阵的填法一一对应

不相交弦问题
在一个圆周上分布着 2n 个点,两两配对,并在这两个点之间连一条弦,要求所得的 2n 条弦彼此不相交的配对方案数
思路
满足
f
n
=
f
0
∗
f
n
−
1
+
f
1
∗
f
n
−
2
+
⋯
+
f
n
−
1
∗
f
0
,
其
中
n
>
=
2
f_n = f_0 * f_{n-1} + f_1 * f_{n - 2} + \cdots + f_{n-1}*f_0,其中n >= 2
fn=f0∗fn−1+f1∗fn−2+⋯+fn−1∗f0,其中n>=2 的一定是卡特兰数

Leetcode 1259:不相交的握手
这题一看样例就知道是卡特兰数
例:典型例题

提升题:电影购票(n和m不同)
当进栈 +1 有 m 个, 出栈 -1 有 n 个时,序列共有 C m + n m − C m + n m + 1 C_{m+n} ^ m - C _ {m + n} ^ {m + 1} Cm+nm−Cm+nm+1种可能性
电影票一张 50 coin,且售票厅没有 coin。m 个人各自持有 50 coin,n 个人各自持有 100 coin。则有多少种排队方式,可以让每个人都买到电影票?
思路
持有 50 coin 的人看作 +1,持有 100 coin 的人看作 -1,类似进出栈问题
与卡特兰数不同的是,这里有 m 个 +1,有 n 个 -1
我们还是可以用折线法来解决这个问题:
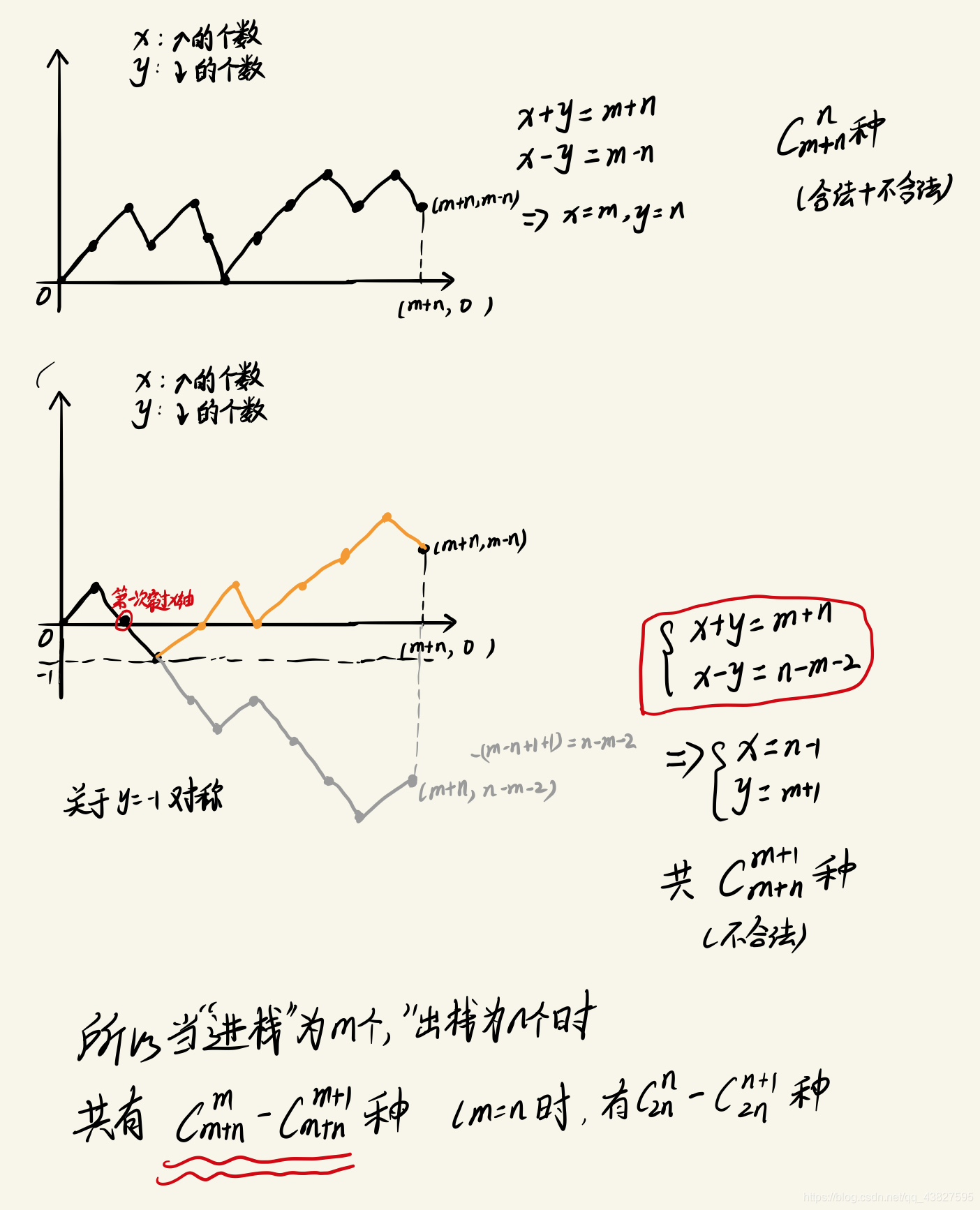
由于排队有先后顺序,所以总共有
(
C
m
+
n
m
−
C
m
+
n
m
+
1
)
∗
m
!
∗
n
!
(C_{m+n} ^ m - C _ {m + n} ^ {m + 1}) * m! * n !
(Cm+nm−Cm+nm+1)∗m!∗n!种可能
注: C m + n m − C m + n m + 1 C_{m+n} ^ m - C _ {m + n} ^ {m + 1} Cm+nm−Cm+nm+1这部分直接推导即可
参考资料
[1] 卡特兰数 — 计数的映射方法的伟大胜利
[2] 【证明】卡特兰数(折线法)
[3] 一道面试题到卡特兰数及其应用
[4] 卡特兰数(catalan数)总结 (卡特兰大数、卡特兰大数取模、卡特兰数应用)
[5] 卡特兰(Catalan)数入门详解 —— 例题的证明讲得不错
[6] LeetCode -「算法入门笔记」卡特兰数

























 6424
6424

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










