12.28---Convergence analysis of some algorithms for solving nonsmooth equations（LiQun Qi）

一、摘要

这篇文章主要讲了一些求解非线性方程( 其中方程具有局部李普希兹的性质)系统的算法收敛性

• 基于方向导数和雅可比的牛顿法，迭代和函数值都是局部超线性收敛
• 在一些假设条件下，由阻尼、基于方向导数的牛顿法产生的点列的极限点是全局收敛的
• 本文提出了一个更一般的定理用于证明收敛性
• 最后提出了一个混合方法，满足全局收敛和局部二次收

二、背景及基础知识介绍

我们考虑一个优化问题

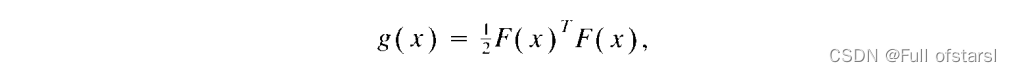
其实就等价于找的解 。

对于求解这样的问题，如果函数F是可微的，就可以直接采用牛顿法 ，有时为了达到全局收敛性，我们还会使用过阻尼牛顿法（利用线搜索技巧确定步长而不是取单位步长）；如果F是不可谓的，通常采用两种策略：采用F的广义雅可比代替F的雅可比、通过求解通过求解

 获得迭代方向.

这篇文章结论的得出需要一些引理的应用，以及一些正则性条件(正则性条件类似于光滑条件下对其导数非奇异的条件)

B-可微：

一个函数F在x点处是B-可微的，如果在这一点处它的方向到处存在并且满足下面这个式子：

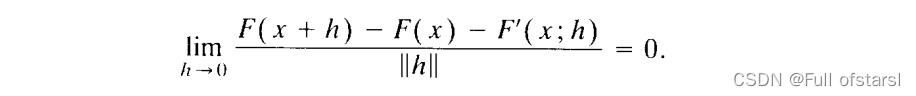
 在一个有限维的欧氏空间中，一个局部李普希兹函数在x点处是B可微函数当且仅当它在x点处方向可微。【REF：On concepts on directional differentiability ;Shapiro】

半光滑： 

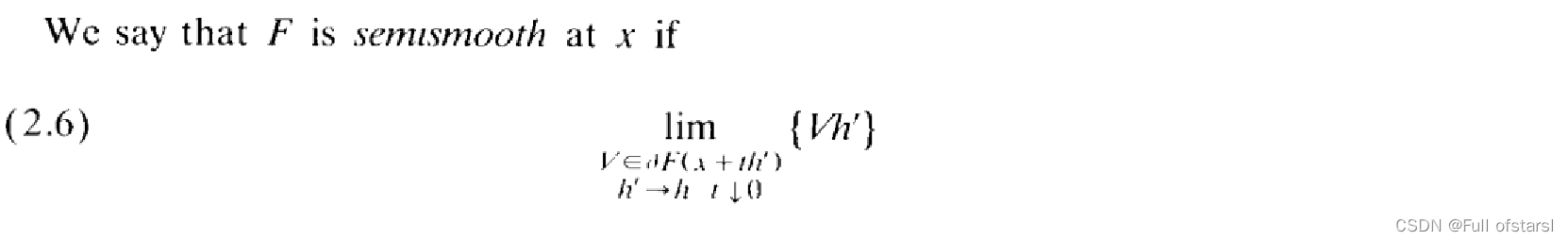
 如果F在x点处是半光滑的，则F在这一点出方向可微并且它的方向导数等于(2.6)式。

在实际应用中很多函数都是半光滑函数，例如常见的非线性互补问题。

BD-正则

 

三、定理介绍

  

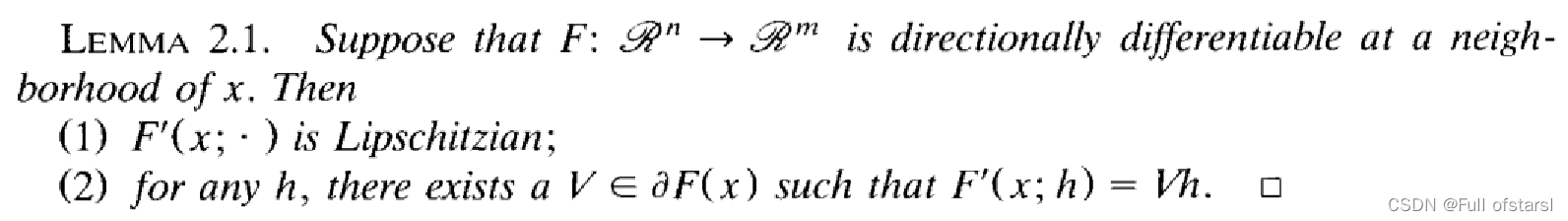
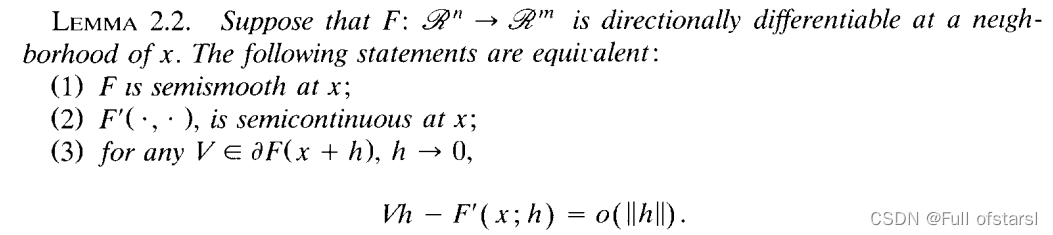
这个引理的证明用到了另外一篇文献的结论，这里给出具体内容

 

  

 

 

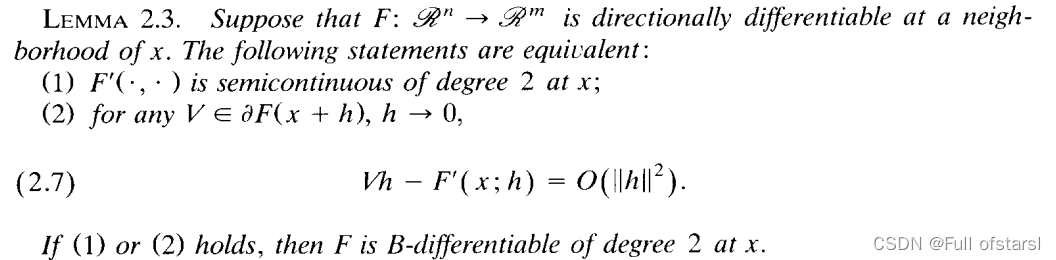
证明思路：利用二阶半连续以及二阶B-可微的定义，结合上面已经证明的引理内容得到结论。其中涉及到放缩部分同样利用了等量代换和凑项的技巧 。

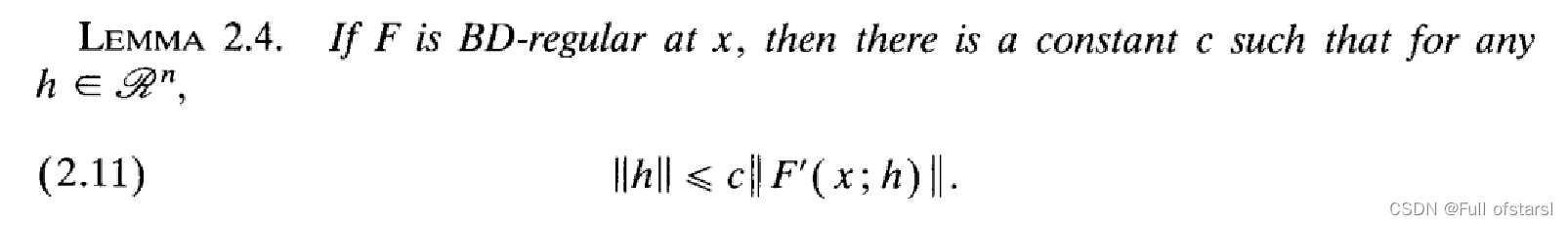
 这一定理是想说明方向导数不为0

证明思路：反证法，假设结论不成立，最后于F满足BD-正则的条件导出矛盾，从而结论得证.

下面是一个关于BD-正则函数的结论