概率论与数理统计——第七周周三-边缘分布律及边缘密度

边缘分布律及边缘密度

引例

1.边缘分布律

以二维表的形式给出：

例1：

设甲、乙两人各进行两次射击，他们每次的命中率分别为0.8和0.6。甲先射击，且甲全部命中时乙的命中率下降
10%，甲全部未命中时乙的命中率上升20%，甲命中1次时 乙不受影响。令X，Y分别表示甲、乙的命中次数， 分别求(X,Y )关于X，Y的边缘分布律

2 . 边缘密度函数

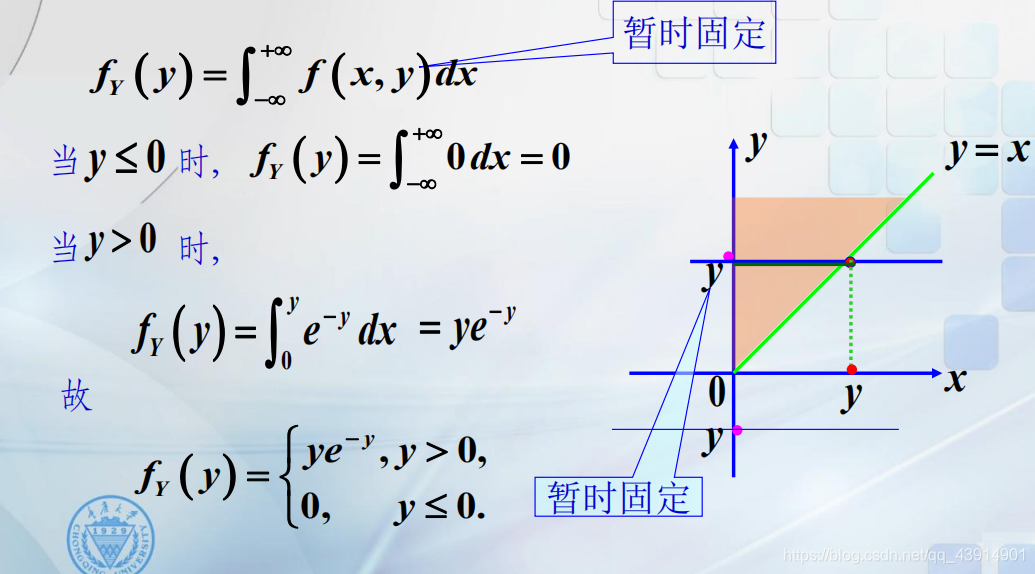
例 2 ：

求解过程 （它的联合密度应该为e 的 -y 次方。）

小练习题：

例1：

例2：

例3：

图解：

二维随机变量的联合密度函数含有丰富的信息，主要有三个方面：
（1）单变量的密度函数，即边缘密度函数；
（2）利用边缘密度函数的信息去判别两个变量之间的相依关系，且利用相关系数去判断它们的相依程度；
（3）当一个变量固定不变时，另一个变量如何变化，具有什么样的密度，这就是条件密度。

因此，确定边缘密度尤为重要。利用二维随机变量的联合密度函数求取边缘密度，在视频和习题中我们已经进行了大量的推演和练习。下面我们将利用图形可视化加深对边缘密度的理解。

clear;clc;
rou=0.3;
[x,y]=meshgrid(-3:0.05:3);
z=(1/(2*pi*sqrt(1-rou^2)))*exp((x.^2+y.^2-2*rou*x.*y)/(-2*(1-rou^2)));
ii=find(x<-1);
z(ii)=zeros(size(ii));
surf(x,y,z)  %画曲面（带切面）
hold on 
iii=find(x==-1);
plot3(x(iii),y(iii),z(iii),'--w','LineWidth',2)  %画截痕
hold on
iiii=find(x==-1.2);
plot3(x(iiii),y(iiii),z(iiii),'--w','LineWidth',2)  %显示截痕所围截面
hold on
text('Interpreter','latex',...
 'String','$$f_X(c)=\int_{-\infty}^{+\infty}{f(c,y)dy}$$',...
 'Position',[-3 1.5 0.17],...
 'FontSize',24)
xlabel('X轴');
ylabel('Y轴');
zlabel('Z轴');
view(3)
%%% 图2的matlab 代码