数学建模——回归分析（上）

回归分析是数学建模的有力工具

由于客观事物内部规律的复杂及人们认识程度的限制,无法分析实际对象内在的因果关系;人们关心的变量(因变量)受另外几个变量(自变量)的关联性(非因果性)的影响，并且存在众多随机因素，难以用机理分析方法找出它们之间的关系；需要建立这些变量的数学模型，使得能够根据自变量的数值预测因变量的大小，或者解释因变量的变化。

例如：

薪金与资历、教育程度、工作岗位 ; 血压与年龄 、血压与年龄

回归分析的主要步骤：

1. 收集一组包含因变量和自变量的数据 选定因变量与自变量之间的模型，利用数据按照最小二乘准则计算模型中的系数；
2. 利用统计分析方法对不同的模型进行比较，找出与数据拟合得最好的模型；
3. 判断得到的模型是否适合于这组数据, 诊断有无不适合回归模型的异常数据；
4. 利用模型对因变量作出预测或解释。

本节主要内容：

从应用角度介绍回归分析的基本原理、方法和软件实现

1. 简化的实际问题及其数学模型
2. 一元线性回归
3. 多元线性回归
4. 非线性回归

实例及其数学模型：

例1 血压与年龄：

为了解血压随年龄增长而升高的关系，调查了30个成年人的血压（收缩压，mmHg）与年龄:

用这组数据确定血压与年龄的关系；
从年龄预测血压可能的变化范围；
回答 “平均说来60岁比50岁的人血压高多少”。

模型建立及求解：

例2 血压与年龄、体重指数、吸烟习惯 ：

又调查了例1中30个成年人的体重指数、吸烟习惯:

模型建立及求解：

例3 软件开发人员的薪金：

建立模型研究薪金与资历、管理责任、教育程度的关系，分析人事策略的合理性，作为新聘用人员薪金的参考.

模型建立及求解：

例4 酶促反应：

酶~高效生物催化剂; 酶促反应~经过酶催化的化学反应； 酶促反应的反应速度主要取决于反应物（底物）的浓度:

底物浓度较小时，反应速度大致与浓度成正比；底物浓度很大、渐进饱和时，反应速度趋于固定值.

为研究酶促反应中嘌呤霉素对反应速度与底物浓度之间关系的影响, 设计了两个实验 :
使用的酶经过嘌呤霉素处理; 使用的酶未经嘌呤霉素处理。

模型建立及求解过程：

一元线性回归的统计分析 ：

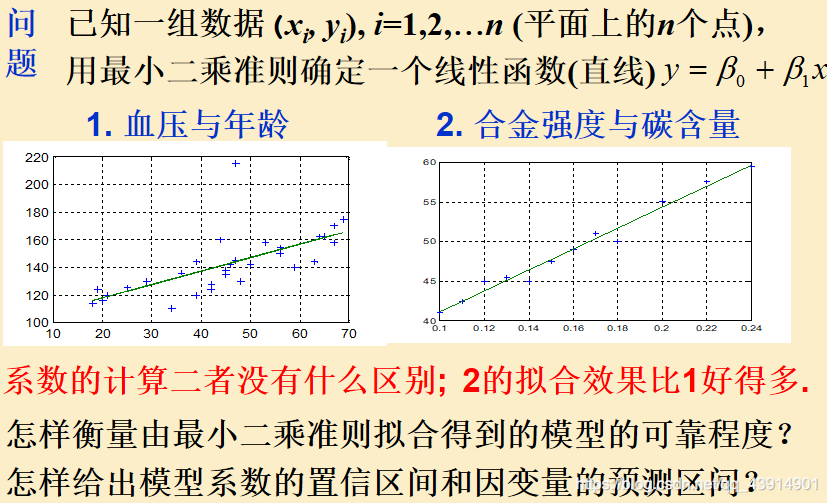
1.一元线性回归模型:

2.回归系数的最小二乘估计:

3.一元线性回归的统计分析:

1.误差方差的估计

2. 回顾系数的区间估计和假设检验

3.模型的有效性检验

4. 利用一元线性回归模型进行预测 :

5. 一元线性回归的MATLAB实现:

实例1——血压与年龄：

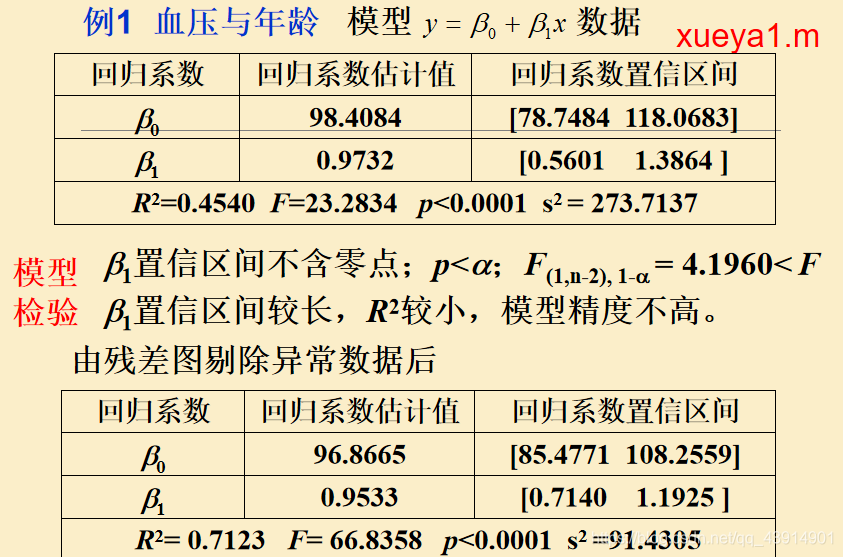
求解结果及其分析：

多元线性回归分析 ：

1 . 多元线性回归模型：

2 . 多元线性回归的统计分析：

1.误差方差的估计

2. 回归系数的区间估计和假设检验

3.模型的有效性检验

4 . 利用多元线性回归模型进行预测:

3 . 多元线性回归的MATLAB实现:

4. 线性最小二乘拟合与多元线性回归的一般形式

5 . 多元线性回归中的交互作用:

例3 软件开发人员的薪金:

- 用残差分析发现交互作用:

matlab代码：

y=[144	215	138	145	162	142	170	124	158	154 162	150	140	110	128	130	135	114	116	124 136	142	120	120	160	158	144	130	125	175];
x=[39	47	45	47	65	46	67	42	67	56 64	56	59	34	42	48	45	18	20	19 36	50	39	21	44	53	63	29	25	69];
n=length(y);
X=[ones(n,1)  x'];
[b,bint,r,rint,s]=regress(y',X);  
b,bint,s,s2=sum(r.^2)/(n-2)   %误差的方差的
rcoplot(r,rint)     %残差的置信区间 
pause
y=[y(1) y(3:30)];
x=[x(1) x(3:30)];
n=length(y);
X=[ones(n,1)  x'];
[b,bint,r,rint,s]=regress(y',X);
b,bint,s,s2=sum(r.^2)/(n-2)
rcoplot(r,rint)
pause
y0=b(1)+b(2)*50;              % 预测y(x=50)
xb=mean(x);
sxx=sum((x-xb).^2);
a=sqrt((50-xb)^2/sxx+1/n+1);
t=tinv(0.975,n-2);
d=t*a*sqrt(s2);
y1=y0-d;y2=y0+d;             % 预测y(x=50)区间（t分布）
[y0 y1 y2]
d1=norminv(0.975)*sqrt(s2);
y3=y0-d1;y4=y0+d1;
[y0 y3 y4]  

代码结果：

>> xueya1
b =
   98.4084
    0.9732
bint =
   78.7484  118.0683
    0.5601    1.3864
s =
    0.4540   23.2834    0.0000  273.7137
s2 =
  273.7137
b =
   96.8665
    0.9533
bint =
   85.4771  108.2559
    0.7140    1.1925
s =
    0.7123   66.8358    0.0000   91.4305
s2 =
   91.4305
ans =
  144.5298  124.5406  164.5190
ans =
  144.5298  125.7887  163.2708