欧拉回路/路径

1.什么是欧拉回路/路径

欧拉路径：在一个图中，由i点出发，将每个边遍历一次最终到达j点的一条路径。
欧拉回路：i=j时的欧拉路径。

2.怎么判断欧拉回路/路径

• 存在欧拉回路/路径前提

• 图是连通的

• 无向图中

在无向图中（连通图），只要每个点的度数（连接的边数）均为偶数，就会存在欧拉回路

因为每个点的度数为偶数，所以可以将整个图看做由数个环嵌套而成，因为环一定能找到一条欧拉回路，所以整个图也能找到欧拉回路。

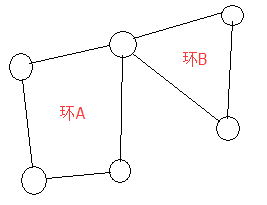
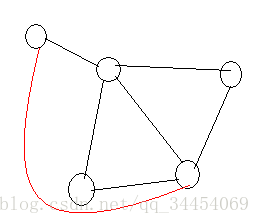
在无向图中（连通图），如果有且仅有两个点的度数为奇数，就会存在一条从这两个中的一个到达另一个的欧拉路径。

假如在这两个点间连一条边，就能够从任意一个点出发找到一条欧拉回路，当出发点为这两个点中的一个时，切断这条边，就成为一条欧拉路径了。

• 有向图中

在有向图中（连通图），只要所有点的入度等于出度，就存在一条欧拉回路。

对于每一个点，每次进入这个节点，就一定有一条路可以出去，因此必定存在一条欧拉回路。

在有向图中（连通图），最多有一点入度等于出度+1，最多有一点入度等于出度-1，就会有一条从出度大于入度（没有则等于）的点出发，到达出度小于入度（没有则等于）的点的一条欧拉路径。

证明方法和无向图的欧拉路径类似。

3.求解欧拉回路/路径

• DFS
  基本思路：在判断出一个图存在欧拉回路/路径后，选择一个正确的起始顶点，用DFS算法遍历所有的边（每一条边只遍历一次），遇到走不通就回退。在搜索前进方向上将遍历过的边按顺序记录下来。这组边的排列就组成了一条欧拉回路/路径。

无向图c++代码

#include <bits/stdc++.h>
#define MAX 2010
using namespace std;
int maps[MAX][MAX];  //邻接矩阵存图
int in[MAX];  //记录每个点度数
int t[MAX];  //存储路径上的点
int flag;
int k;
int Max,Min;
int DFS(int x)
{
    int i;
    for(i=Min;i<=Max;i++)
    {
        if(maps[x][i])///从任意一个与它相连的点出发
        {
            maps[x][i]--;///删去遍历完的边
            maps[i][x]--;
            DFS(i);
        }
    }
    t[++k]=x;///记录路径，因为是递归所有倒着记
}
int main()
{
    int n,i,x,y;
    Max=-9999;
    Min=9999;
    flag=0;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
    {
        scanf("%d%d",&x,&y);
        maps[x][y]++;
        maps[y][x]++;
        Max=max(x,max(y,Max));
        Min=min(x,min(y,Min));
        in[x]++;
        in[y]++;
    }
    for(i=Min;i<=Max;i++)
    {
        if(in[i]%2)///存在奇度点，说明是欧拉路径，并且从该点开始找
        {
            flag=1;
            DFS(i);
            break;
        }
    }
    if(!flag)///全为偶度点，从标号最小的开始找
    {
        DFS(Min);
    }
    for(i=k;i>=1;i--)
    {
        printf("%d\n",t[i]);
    }
    return 0;
}

注意点：由于dfs是在回溯的时候存点，所以输出的时候要倒着遍历，或者把点存在一个栈里（先进后出）

• Fleury(佛罗莱)算法

设G 为一无向欧拉图，求G 中一条欧拉回路的算法为：

1. 任取G 中一顶点v0，令P0 = v0；
2. 假设沿Pi = v0e1v1e2v2 …eivi 走到顶点vi，按下面方法从E(G) - { e1, e2, …, ei }中选ei+1：
   a) ei+1 与vi 相关联；
   b) 除非无别的边可供选择，否则ei+1 不应该是Gi = G - { e1, e2, …, ei }中的桥。
3. 当2)不能再进行时算法停止。

可以证明的是，当算法停止时，所得到的简单回路Pm = v0e1v1e2v2 …emvm, (vm = v0)为G 中一条 欧拉回路。

桥：设无向图G(V, E)为连通图，若边集E1⊆E，在图G 中删除E1 中所有的边后得到的子图是不连
通的，而删除了E1 的任一真子集后得到的子图是连通图，则称E1 是G 的一个割边集。若一条边
构成一个割边集，则称该边为割边，或桥。

基本思路：按顺序依次dfs找点连边，找到一条边后就删除此边，在找点连边的时候，除非无路可走，才去走桥。
无向图c++代码

#include <bits/stdc++.h>
using namespace std;
int ans[200];
int top;
int N,M;
int mp[200][200];
void dfs(int x)
{
    int i;
    top++;
    ans[top]=x;
    for (i=1; i<=N; i++)
    {
        if(mp[x][i]>0)
        {
            mp[x][i]=mp[i][x]=0;///删除此边
            dfs(i);
            break;
        }
    }
}

void fleury(int x)
{
    int brige,i;
    top=1;
    ans[top]=x;///将起点放入Euler路径中
    while(top>=0)
    {
        brige=0;
        for (i=1; i<=N; i++) /// 试图搜索一条边不是割边（桥）
        {
            if(mp[ans[top]][i]>0)///存在一条可以扩展的边
            {
                brige=1;
                break;
            }
        }
        if (!brige)/// 如果没有点可以扩展，输出并出栈
        {
            printf("%d ", ans[top]);
            top--;
        }
        else     /// 否则继续搜索欧拉路径
        {
            top--;///为了回溯
            dfs(ans[top+1]);
        }
    }
}

int main()
{
    int x,y,deg,num,start,i,j;
    scanf("%d%d",&N,&M);
    memset(mp,0,sizeof (mp));
    for(i=1;i<=M; i++)
    {
        scanf("%d%d",&x,&y);
        mp[x][y]=1;
        mp[y][x]=1;
    }
    num=0;
    start=1;///这里初始化为1
    for(i=1; i<=N; i++)
    {
        deg=0;
        for(j=1; j<=N; j++)
        {
            deg+=mp[i][j];
        }
        if(deg%2==1)///奇度顶点
        {
            start=i;
            num++;
        }
    }
    if(num==0||num==2)
    {
        fleury(start);
    }
    else
    {
        puts("No Euler path");
    }
    return 0;
}

注意点：此代码是一边找边一边输出路径上的点，也可以把点保存后再输出。

4.欧拉回路/路径的应用

• 一笔画问题
• 洛谷P1341
  基本思路：求字典序最小的一条欧拉回路/路径，dfs过程其实就是不停地找字典序较小的边。另外要判断图是否是连通的（可以用并查集解决）。其他一些细节自己看代码斟酌，偷懒不想打注释了（挨打）
  参考AC代码

#include <bits/stdc++.h>
using namespace std;
int n,dep[125],e[125][125],fa[125];
char ans[1330];

void dfs(int x){
	for(int i=65;i<=122;i++){
		if(e[x][i]){
			e[x][i]=e[i][x]=0;
			dfs(i);
		}
	}
	ans[n--]=x; 
}

int find(int x){
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}

void unite(int x,int y){
	fa[find(x)]=find(y);
}

int main(){
	cin>>n;
	for(int i=65;i<=122;i++) fa[i]=i;
	for(int i=0;i<n;i++){
		string s;
		cin>>s;
		e[s[0]][s[1]]=e[s[1]][s[0]]=1;
		unite(s[0],s[1]);
		dep[s[0]]++;dep[s[1]]++;
	}
	int cnt=0;
	for(int i=65;i<=122;i++) if(fa[i]==i&&dep[i]) cnt++;
	if(cnt!=1) {
		cout<<"No Solution";
		return 0;
	}
	cnt=0;
	int head=0;
	for(int i=65;i<=122;i++){
		if(dep[i]&1){
			cnt++;
			if(!head) head=i;
		}
	}
	if(cnt&&cnt!=2){
		cout<<"No Solution";
		return 0;
	}
	if(!head){
		for(int i=65;i<=122;i++)
		if(dep[i]){
			head=i;
			break;
		}
	}
	dfs(head);
	cout<<ans;
	return 0;
}

另：并查集是个好东西（滑稽），不懂的可以去参考我上上篇博客，传送门。

至此，欧拉回路/路径已经总结完了（大呼一口气）花了半上午

如果想要得到更多知识，请关注我博客：wlis.blog.csdn.net

此博客不定期更新内容！！！感谢大家！！！