abaqus黑盒猜测和理论学习： S4R 单元的实现方式 板壳、梁理论

对称的壳单元（位于theory介绍壳体的较前部分）

对称的壳单元的6个假设

abaqus关于AXISYMMETRIC shell element的theory6个假设，可以看到实际上对称的壳单元满足Kir直法线假设
但以实验为准，见博主这篇博文，S4R单元（并不属于thin ,按abaqus属于general的范畴）的3轴应力应变都是0。
事实上，应力为0是因为S4R单元是结合了平面应力假设+Kir直法线假设的壳元.

abaqus 有限应变壳单元理论学习 重点学习S4R

S4R理论

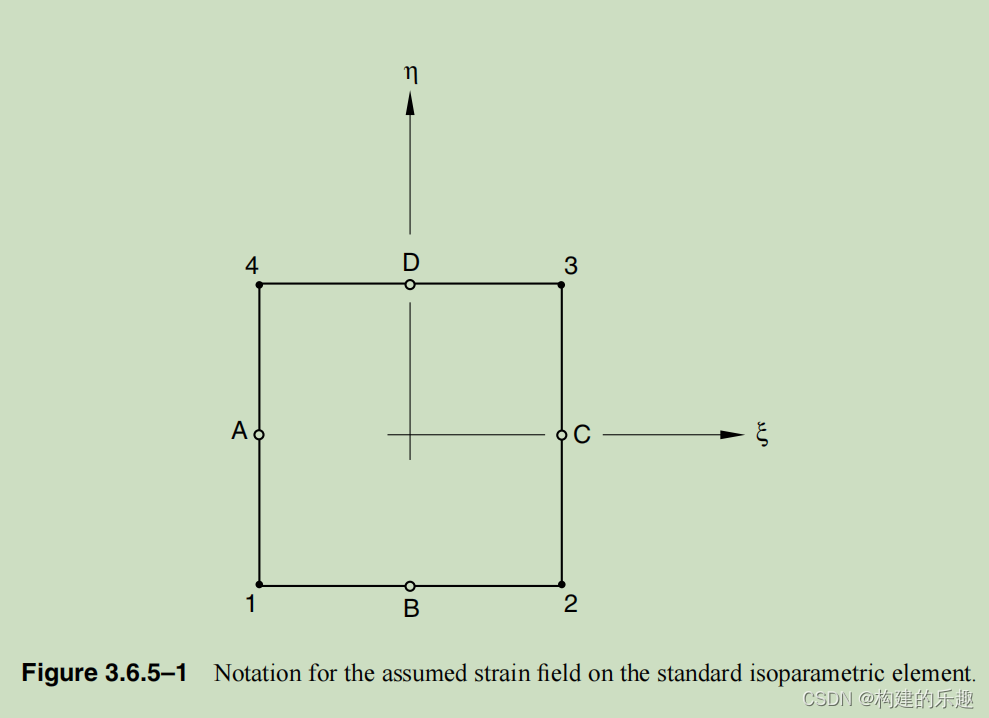
看了一下abaqus 《theory》 3.6.5。
里面实际是连续介质力学的内容，讲了各个量——如法向量、曲率随时间的更新公式等。
此外还有上图开始讲了能预防剪切自锁的strain field formulation，并推导出了S4R这一类finite strain单元的
stiffness matrix，这是我真正需要的。但是Ks并不是刚度，它的单位是应力。Cs is the transverse shear stiffness

finite strain单元 3.6最后：

Element S4 is a fully integrated finite-membrane-strain shell element. Since the element’s stiffness is fully integrated, no spurious membrane or bending zero energy modes exist and no membrane or bending mode hourglass stabilization is used. Drill rotation control, however, is required. Element S4 uses the same drill stiffness formulation as used for element S4R. Similarly, element S4 assumes that the transverse shear strain (and force, since the transverse shear treatment is elastic based on the initial elastic modulus of the material) is constant over the element. Therefore, all four stiffness integration locations will have the same transverse shear strain, transverse shear section force, and transverse shear stress distribution. The transverse shear treatment for S4 is identical to that for S4R.

It is well known that a standard displacement formulation will exhibit shear locking for applications dominated by in-plane bending deformation. However, a standard displacement formulation for the out-of-plane bending stiffness is not subject to similar locking response.Hence, S4 uses a standard displacement formulation for the element’s bending stiffness, and the theory presented above for the rotation kinematics and bending strain measures applies to S4. The primary difference between the element formulations for S4 and S4R is the treatment of the membrane strain field. This formulation is the topic of the following discussion.

The membrane formulation used for S4 does not rely on the fact that S4 is a shell element. Hence, the discussion below details the formulation from the point of view that the membrane response is governed by the equilibrium for a three-dimensional body in a state of plane stress.

1.standard displacement formulation?
2.why “a standard displacement formulation for the out-of-plane bending stiffness is not subject to similar locking response”?
3.What is a membrane formulation, what is finite-membrane-strain ?
薄膜应变就是面内的那三个应变。剩下三个叫transverse shear strain。
abaqus theory前面40页也很重要，很基本的.

initial stress:预应力

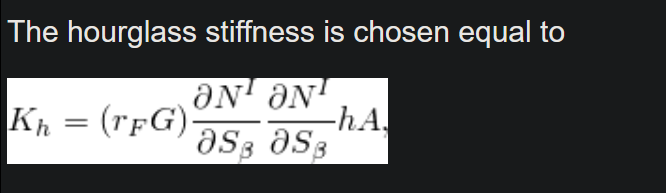
我的手稿地址：
https://github.com/BraveDrXuTF/S4R_theoryPDF

通过这个锻炼，找到一个abaqus乃至其他CAE软件复杂文档的组成逻辑，帮助以后的阅读查找工作。

想要参考abaqus壳更多的内容，可以看analysis 29章，里面对于各类单元的讲解很详细。

经典的板壳力学教材和上课讲的东西能否成为突破口？结合看一下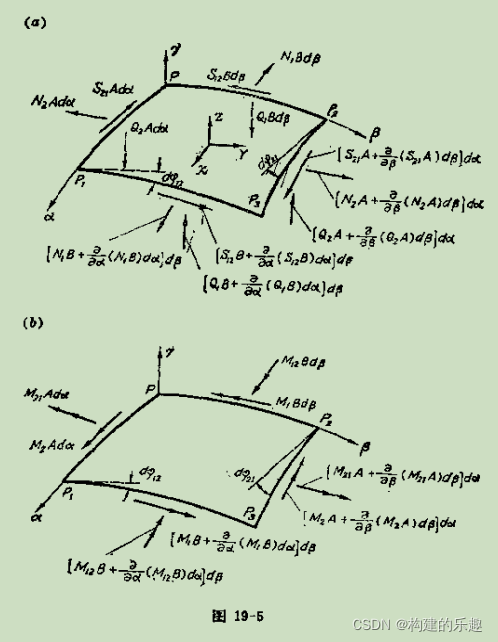

图片来自于徐芝纶的《板壳力学》

我或许还需要N1,N2,M1,M2等数据
找到了RF,RM系列数据

什么叫薄膜内力？

轴对称壳元

轴对称壳元（s,$\theta$两个坐标即可确定壳体内一点位置）的薄膜状态和弯曲状态，壳元的内力是有分类的，分为薄膜内力和弯曲内力：

轴对称斜锥壳元：

轴对称截锥壳元：以直代曲

几何方程—B—K

考虑横向剪切的轴对称壳体理论基本原理：

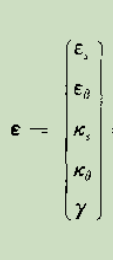
比不考虑横向剪切多了个$\gamma$.
考虑剪切变形的梁称为铁木辛柯梁。——有限单元法9.2.4
挠度和截面转角独立插值的称为铁木辛柯梁单元。——有限单元法9.2.4

保证K2奇异，K1非奇异，这样才能使极限情况下方程仍然有非零解。怎么理解？——有限单元法8.5节

我的理解（不一定正确）：极限情况下K2占据主导地位，方程(K1+K2)a=F退化为K2a=0，K2奇异才能有非零解。

位移和转动独立插值的截锥壳元

原理和铁木辛柯梁单元一样，也需要保证K2奇异，K1非奇异。

本科学的梁单元是不考虑剪切变形的梁单元，即《有限单元法》9.2.3节

考虑剪切变形有两种方式

1.叠加

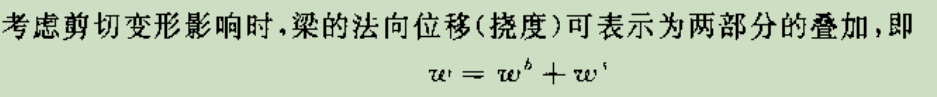
wb部分方程和本科学的梁单元一样,ws代表剪切部分引起的附加法向位移，它的方程比较简单

2.铁木辛柯梁单元

分别插值。

考虑层间应力无法直接应用S4R，但可以加弹簧

http://www.doc88.com/p-9921475056045.html

声明：

近日作者发现，有部分网站：
https://wenku.baidu.com/view/70282ae40f22590102020740be1e650e52eacf01.html
https://www.pudn.com/news/623f187f2cfc38172120b885.html
在未通知作者的情况下以不恰当的方式转载了本文，将本文变为下载需要收费的文章，没有注明原作者和原始来源。并且第一个网址抹除了图片的水印，在此作者给予强烈的谴责，并保留追责的权利。
根据CC BY-SA 4.0协议，转载本文，必须附上原始作品的来源及本许可证的链接。

20220906

这一块的话，没想到S4R如此神通广大，竟然有如此的formulation。

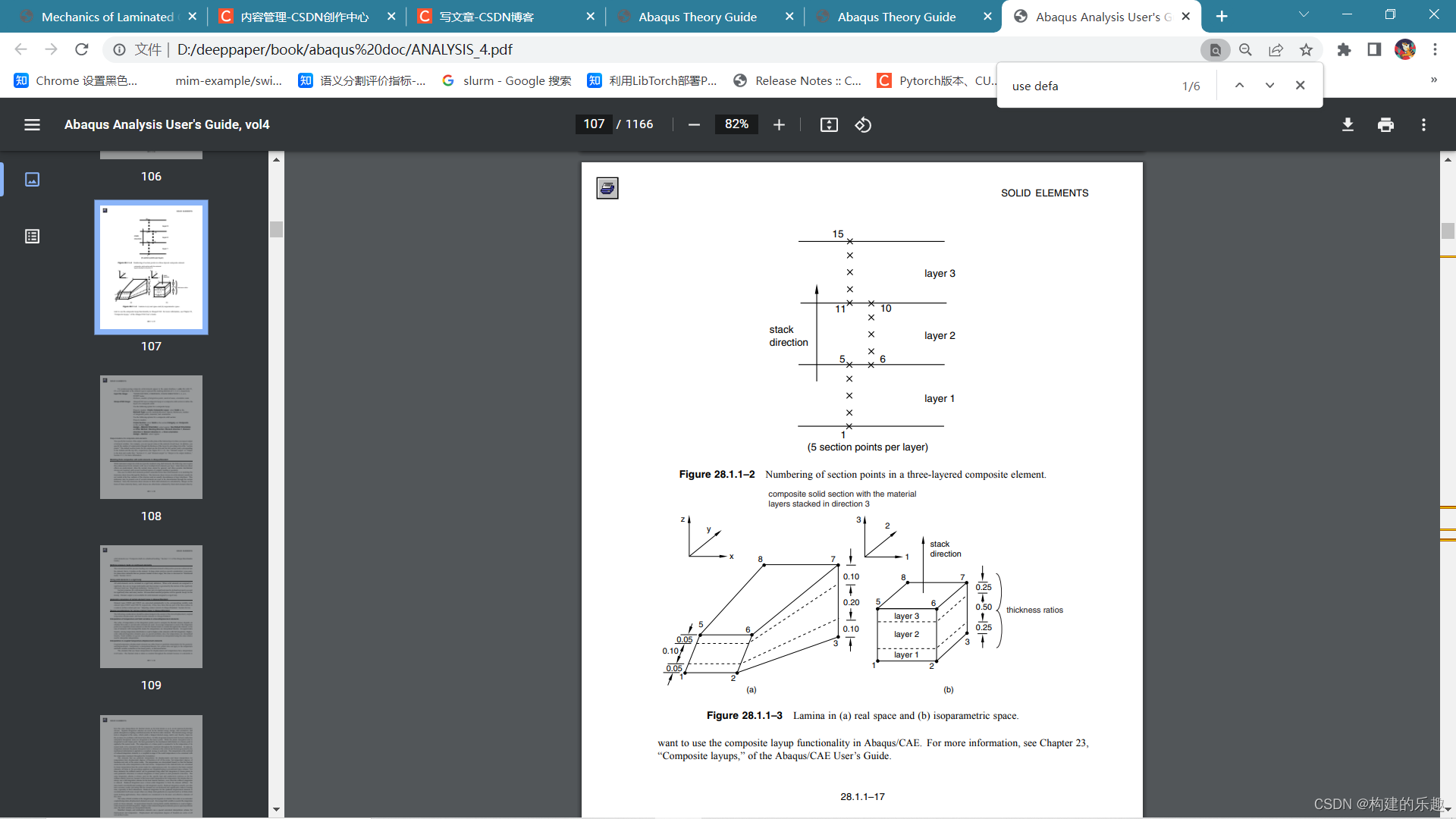
3D单元复合材料建模，在文档abaqus analysis 4。

20220908

没想到啊没想到，S4R的层中是有TSHR13和23的。在上下边界这两个值则为0.
在下边界，我试了一阶剪切的strain formulation是符合abaqus的结果的，在里面-0.6667的位置，我的小算例printabaqus.py是符合的，而大规模test_data.py则暂时不符合：

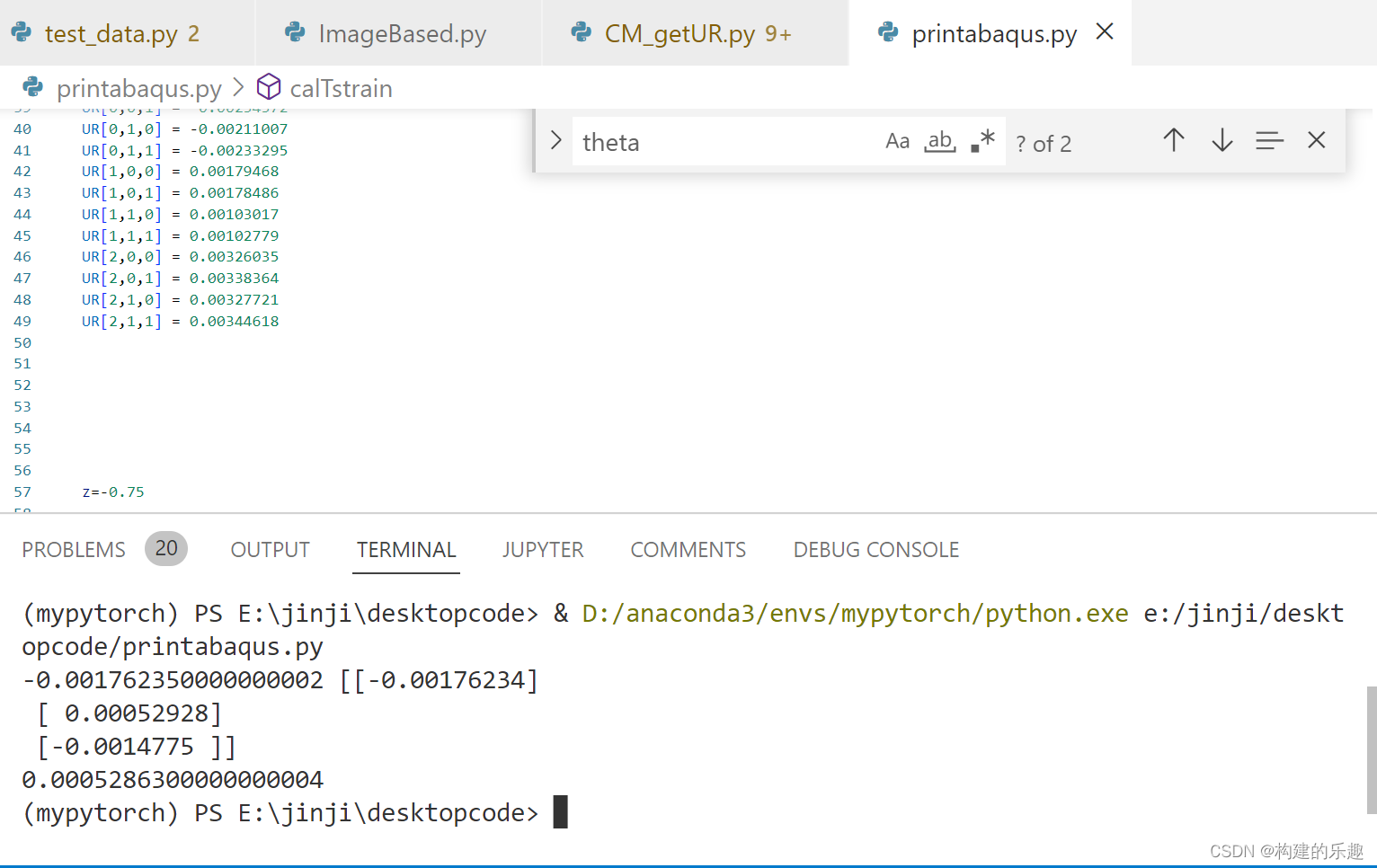
20221031：S4R的厚度方向默认是3个积分点（亲测），而不是5个。

以4层为例，将section_num_tuple改为(1,2，…13)倒也不会报错，但是，odb中只会有12个积分点的结果。

20221104

成功验证abaqus S4R 单元在多层变刚度平板下使用的是一般壳理论。

20221124

成功校对abaqus S4R平板大部分位置的应变能。我还计算了特定工况下的外力做功，应变能-外力功=总势能。
但是有一点很奇怪，边界的平衡方程量严重的对不上，我想abaqus在其中定有计较，有可能涉及到沙漏控制等等。

上图是abaqus平板的平衡方程量，不是应变能哈。如图，大部分都对上了（平衡方程量=0就是对上了），边界的严重对不上。

20231003

https://zhuanlan.zhihu.com/p/150767487
这篇文章很好，也许真的是沙漏的问题

通过如下代码关闭了沙漏：

    elemType1 = mesh.ElemType(elemCode=S4R, elemLibrary=STANDARD, 
        secondOrderAccuracy=OFF, hourglassControl=RELAX_STIFFNESS, 
        displacementHourglass=0.0, rotationalHourglass=0.0)
    elemType2 = mesh.ElemType(elemCode=S3, elemLibrary=STANDARD)
    p = mdb.models['Model-1'].parts['mengpi_real']
    f = p.faces
    faces = f.getSequenceFromMask(mask=('[#1 ]', ), )
    pickedRegions =(faces, )
    p.setElementType(regions=pickedRegions, elemTypes=(elemType1, elemType2))

之后我写的迭代法求解器与abaqus求解的结果能够很好的对上了。