树表的查找
对于前面所述的线性表的查找方式的分析,线性表查找不适用于动态查找表(即表不断被修改)。若要对动态查找表进行高效率的查找,可采用几种特殊的二叉树作为查找表的组织方式,统称为树表。
二叉排序树
二叉排序树又称二叉查找树,它对于排序和查找都很有用的特殊二叉树。
二叉排序树的递归定义:
(1)若它的左子树不为空,那么左子树上的所有结点的值都小于根结点
(2)若它的右子树不为空,那么右子树上的所有结点的值都大于根结点
(3)对左子树和右子树进行同样操作。
通过定义可以知道,对于二叉排序树,我们进行中序遍历得到的序列是一个增序数列。
二叉排序树的数据结构
#define infotype int
typedef struct {
keytype k;
infotype info;
}Item;
typedef struct Bnode {
Item e;
struct Bnode* Lnode, * Rnode;
}BSnode,*BStree;
二叉排序树的查找
前面介绍线性表的查找的时候介绍过的折半查找时,介绍过排序过程类似于二叉排序,所以二叉排序树的查找过程也和折半查找类似。
BStree search_bs(BStree T, keytype k) {
if ((!T) || T->e.k == k) //为空或者根结点值匹配成功
return T;
else if (T->e.k < k) //值比根结点大,比较右子树
return search_bs(T->Rnode, k);
else //值比根结点小,比较左子树
return search_bs(T->Lnode, k);
}
算法分析
- ASL
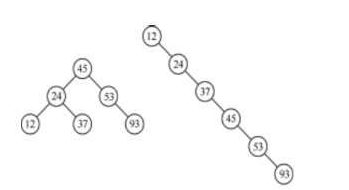
通过对于排序二叉树的学习,我们知道,二叉排序树的构成由原始序列的排序决定,如果输入的序列是一个递增序列,那么我们得到的二叉排序树就是一直时右子树的树,也就是一条线。如下图对于一个序列不同输入方式时。
那么可以得出最优的情况,二叉排序树的ASL等于折半查找的ASL;相反情况为顺序查找的ASL。
2.优点:相较于折半查找的顺序存储结构,二叉排序树在动态查找表中具有更好的效率,只需修改树结点的指针便可以实现插入删除。
二叉排序树的动态修改
- 二叉排序树的插入
//插入
void Insert_bsT(BStree &T, TItem e) {
//因为二叉排序树的插入必定最后必会被添加到树中一个叶子结点中原本为空的左或右孩子,所以递归实现
if (!T) { //若根结点为空,将结点插入
BStree s = new BSnode;
s->e = e;
s->Lnode = s->Rnode = NULL;
T = s;
}
else if (e.k < T->e.k) //小于,左子树
Insert_bsT(T->Lnode, e);
else if (e.k > T->e.k) //大于,右子树
Insert_bsT(T->Rnode, e);
}
- 二叉排序树的创建
//创建
void Create_bsT(BStree& T) {
T = NULL;
printf("输入k值:");
TItem e = {};
scanf_s("%d", &e.k);
while (e.k != 0) {
Insert_bsT(T, e); //用插入的方法创建
printf("输入k值:");
scanf_s("%d", &e.k);
}
}
- 二叉排序树的删除
二叉排序树的删除时最复杂的
考虑三种情况:
①被删除结点为叶子结点:直接删除,修改其双亲结点指针。
②被删除结点只有一棵左子树或者右子树:直接将其左子树或右子树链接给其双亲结点。
③被删除结点有左子树和右子树
如下图:对于这样的结构,我们有两种方法:一、将被删除结点的左子树链接给其双亲结点,再将其右子树链接到其左子树的右子树上;二、我们知道对于二叉排序树的中序遍历是一个递增数列,那么将被删除结点的在这个递增数列中的前驱(或后驱结点)代替该结点,然后删除其前后(或后驱结点)。当然该前驱结点可能存在左子树,将左子树赋给它的双亲结点。
对比两种方法,第一种可能会增加树的深度,对于二叉排序树的查找来说,增加树的深度会使得ASL变大,所以采用第二种来实现。
//删除
void delete_bsT(BStree& T, keytype k) {
BStree P = T, F = NULL, q = NULL;
while (P) { //查找该结点,并辅助F为其双亲结点
if (P->e.k == k)
break;
F = P;
if (P->e.k > k)
P = P->Lnode;
else
P = P->Rnode;
}
if (!P) //查找失败
return;
//被删除结点的左、右子树都存在
if (P->Lnode && P->Rnode) {
BStree S = P->Lnode;
q = P;
while (S->Rnode) {
q = S;
S->Rnode;
}
P->e = S->e;
//前驱结点有右子树的情况,将前驱结点的左子树赋给前驱结点双亲结点的右子树
if (q != P) {
q->Rnode = S->Lnode;
}
else //前驱结点没有右子树的情况,直接将前驱结点的左子树赋给被删除结点的左子树
q->Lnode = S->Lnode;
return ;
}
//被删除结点的左子树存在
else if (!P->Rnode) {
q = P;
P = P->Lnode;
}
//被删除结点的右子树存在
else if (!P->Lnode) {
q = P;
P = P->Rnode;
}
//链接到双亲结点
if (!F) //删除根结点
T = P;
else if (q == F->Lnode) //被删除结点为双亲结点左子树(被删除结点只含左或右子树)
F->Lnode = P;
else //被删除结点为双亲结点右子树(被删除结点只含左或右子树)
F->Rnode = P;
}
平衡二叉树
前面所述的二叉排序树的查找算法效率决定于树的深度,也就是二叉排序树的结构,取决于创建二叉排序树的数据集。就如前面所述,若数据集为一个增序数列,那么得到的排序二叉树就是一个线性结构(树的深度达到最大值),ASL就是顺序查找的效率。那么树的深度越小,查找速度就越快。为了使创建的二叉排序树深度不受数据集的排序序列的影响能够达到深度最小算法最优,下面介绍一种特殊的二叉排序树,平衡二叉树(AVL树)。
平衡二叉树的定义
不为空树时有以下特征
①左子树和右子树的深度之差的绝对值不超过 1
②左子树和右子树也是平衡二叉树
可以发现平衡二叉树极大的满足了排序二叉树数据集个数 n 时达到算法效率最优log2n
平衡二叉树的实现
简单叙说,平衡二叉树就是在利用数据集创建二叉排序树时通过一些规则来修改二叉排序树的形状使得树的深度最小。从而提高查找算法效率
- 两个关键概念
① 平衡因子(BF):结点的BF被定义为左右子树的深度之差。
引进这个概念是通过BF绝对值超过 1 时,会形成不平衡树。
② 最小不平衡树:插入一个结点时,会改变其所有祖先结点的BF,以距离插入结点最近的祖先结点为根构成的树,就是最小不平衡树。
设想如果树很大,添加一个结点可能会对其所有祖宗结点的BF造成影响,那么我们通过解决最小的这棵不平衡树来解决总体的不平衡性。所以引进这个概念是为了通过优化局部问题来解决全局问题。
- 分析形成最小不平衡树的情况 ,得到修改规则
①LL型:在结点 A 的左子树根结点的左子树插入结点,使得 以 A 为根的树形成最小不平衡树(如图的结点 5 )。
问题 1 : 局部影响了整体,修改局部也就是最小不平衡树。修改的本质是使得最小不平衡树(图中黄色框内)变成平衡树。那么,怎么改变?
分析:对于最小不平衡树的根结点来说,它的BF为 2 ,说明导致不平衡是因为它的左子树的深度比右子树的深度大 2 。要想平衡那么很简单,左子树深度减 1 ,右子树深度加 1 ,那么根结点的BF就为 0 了。如同扁担,左边重了,那么将中心向左边移动。所以将不平衡树的根结点变为其原来的左子树中的结点。
将左子树的根结点变为最小不平衡树的根结点,左子树深度减 1 ;将最小不平衡树的根结点变为右子树根结点,右子树深度加 1
问题 2 : 最小不平衡树的原根结点会变成它的原左子树根结点的右子树根结点,那么它的原左子树根结点的右子树应该何去何从(如图的结点 4 )?
操作: 顺时针旋
书上模型定义:
②RR型:根结点右子树根结点的右子树插入结点。
不难知道,RR型就是LL的对称模型,对于不平衡树来说,顺时针将根结点的BF变小,那么逆时针就是变大。
操作: 逆时针旋转
书上模型定义:
③LR型:根结点左子树根结点的右子树插入结点。
根据插入结点是根结点左子树根结点的右子树的左子树还是右子树,可以分为LR( L ),LR( R )。操作上没有区别,会对结点的BF产出不同。
分析: 根据LL型和RR型我们可以知道,当 BF 为负时,左子树深度小于右子树,可以将树逆时针旋转使得根结点BF增加;相反,当 BF 为正时,左子树深度大于右子树,可以将树顺时针旋转使得根结点BF增加。对于LR型,我们先对最小不平衡树根结点的左子树逆时针旋转使得其变为LL型再顺时针旋转。
操作:先逆时针再顺时针
书上实例:
书上模型定义:
④RL型:根结点左子树根结点的左子树插入结点。
分析: 根据LL型和RR型我们可以知道,当 BF 为负时,左子树深度小于右子树,可以将树逆时针旋转使得根结点BF增加;相反,当 BF 为正时,左子树深度大于右子树,可以将树顺时针旋转使得根结点BF增加。对于RL型,我们先对最小不平衡树根结点的右子树顺时针旋转使得其变为RR型再逆时针旋转。
操作:先顺时针再逆时针
相同的RL也分为RL(L)和RL(R)
书上实例:
书上模型定义:
算法分析
平衡二叉树是使得二叉排序树的形成的树结构的深度最小,从而使得查找效率最优log2n。对于出现最小不平衡二叉树的四种情况可以发现其中 根结点和其左子树(或右子树)在BF值上的规律。
规律:
插入一个结点时:
(1)若e的关键字小于根结点的关键字,则将e插入在根结点的左子树上,插入后左子树深度+1时,不同情况处理:
①根结点的BF为−1(右子树的深度大于左子树的深度):则将根结点的平衡因子更改为0,整个二叉排序树的深度未变,不需要修改全部祖宗结点BF 。
②根结点的BF为0(左、右子树的深度相等):则将根结点的平衡因子更改为1,整个树深度增1,需要修改其全部祖宗结点的 BF ;
③根结点的BF为1(左子树的深度大于右子树的深度):若根结点的左子树根结点的BF为1(LL型),则需进行顺时针平衡处理,将根结点和其右子树根结点的平衡因子更改为0,整个树的深度不变;若根结点的左子树根结点的BF为−1,则为LR型,旋转处理之后。修改根结点和其左、右子树根结点的BF,树的深度不变。
(2)若e的关键字大于根结点的关键字,则将e插入在根结点的右子树上,根据根结点的BF值,确定为RR还是RL的类型来进行和(1)类似操作。
B-树
前面所述的查找算法都是在内存中进行的,适用于较小的文件。对较大的、存放在外存储器中的文件,被称为 B 树的多路平衡查找树。它适合在磁盘等直接存取设备上组织动态的索引表,适应文件查找和动态变化。
- B-树的定义
一颗 m 阶 B- 树或为空树,或满足下列特性:
①树中每个结点至多有m棵子树;
②若根结点不是叶子结点,那么至少有两棵子树;
③除根结点外的所有非终端结点至少有[ m/2 ]棵子树;(多路的特性)
④所有的叶子结点都出现在同一层次。(平衡的特性)
⑤所有非终端结点最多有 m-1 个关键字,关键字有序(有序的特性)
结点的结构如下。其中 Ki (0 < i <= n)为关键字,Pi (0 <= i <= n)为指向子树根结点的指针。其中 Pi所指向的树中所有结点关键字小于Ki+1 (0 <= i < n)
- B-树的查找
由定义可知,查找过程和二叉排序树的过程类似。
查找步骤:
①对于跟定关键字 K 与根结点所有关键字比较,由于B-树的有序性,所以查找可以用顺序或折半查找。
②查找时,如 K 与结点关键字相同,则查找成功,否则③
③若 K 小于 K1 ,则将指向 P0 所指向的子树;
若 Ki < K < Ki+1 (0 < i < n),则将指向 Pi 所指向的子树;
若 Kn < K ,则将指向 Pn 所指向的子树;
查找效率
- 由查找过程分为两部分:1.找到结点;2.找到关键字。
由于关于结点的信息是存储在外存等存取设备上,找到结点后将信息调入内存进行关键字的查找。因为内外存交换的时间损耗远大于关键字查找(顺序或折半查找)。所以主要分析在内存中找到结点的效率,而查找过程类似二叉排序树,分析树的层次深度就是查找结点的个数。- 分析深度为 h+1 含有 N 个关键字的 m 阶 B- 树的最大深度:
①按照 B- 树的定义。第一层至少有 1 个结点;第二层最少有 2 个结点;第三层最少有 2 * ([ m/2 ])个结点(非终端结点最少有[ m/2 ]棵子树);以此类推。h+1层至少有 2 ✖( [ m/2 ]的h-1次方)。
②含有 N 个关键字,那么叶子结点的个数为 N+1 。
对于一棵含有 N 个关键字的B-树,无论它的阶数,其叶子结点都可以通过将其合并最后得到一个含有 N 个关键字结点。由于定义,所以叶子结点个数为 N+1 .
因为 h+1 层为叶子结点层,而前得出其最少结点个数为2 ✖( [ m/2 ]的h-1次方),且通过 N 个关键字得出的结点个数为 N+1,所以
即含有 N 个关键字的B-树查找时查找的结点数不超过:
- B-树的添加删除
①添加
由于B-树时动态查找树,生成过程由空树开始,在查找过程中通过逐个插入关键字得到。由于定义我们知道,对于每个结点的关键字个数的要求,所以插入关键字不是单纯的添加结点,而是在最底层的非终端结点中添加关键字。对于插入情况分两种:
①对于非终端结点关键字个数添加关键字后不超过定义最大值,则插入成功
②反之,则将该非终端结点以中间关键字为界分为两个结点。并把中间关键字向上插入到双亲结点上。若双亲结点的关键字个数超出,重复该步骤。最坏分解根结点,致使树的深度+1.
书上实例:
②删除
- 由于删除关键字必然会影响到结点的关键字个数低于最小值,和指向子树的指针。而删除关键字的结点分为两种:
①是叶子结点上一层的非终端结点,如删除后关键字个数不低于最小值,直接删除关键字和其右边指针;
②反之,则根据B-树特性将关键字右边指针所指子树中的最小关键字来代替删除关键字。- 因此,只讨论叶子结点上一层的三种情况:
①被删除关键字所在结点关键字数目不低于[ m/2 ] ,只需删除关键字和右边指针。
②被删除关键字所在结点关键字数目等于[ m/2 ]-1 ,且结点相邻左兄弟(右兄弟)中的关键字数目大于[ m/2 ]-1 ,则将兄弟结点中的最大值(最小值)关键字替换双亲结点中大于(小于)且紧靠该关键字的关键字下移替换被删除关键字。
③被删除关键字所在结点和其相邻的兄弟结点的关键字数目都等于[ m/2 ]-1 。若其有兄弟结点且由双亲结点关键字 Ki 的右指针 Pi 所指向,删除关键字后,将结点内剩余关键字和指针加上 Ki 一起合并到 Pi 所指的兄弟结点中。如果操作后双亲结点的关键字数目低于[ m/2 ]-1 ,再类推进行操作。
实例:
B+树
B+树是B-树的变形树。一颗 m 阶B+树和B-树的差异在于:
①结点有n个关键字就有n棵子树
②所有的叶子结点中包含了所有的关键字信息,以及指向含这些关键字记录的指针,而叶子结点本身依关键字的大小自小而大顺序链接。
③所有的非终端结点可以看作为索引,仅含其子树的中最大(或最小)关键字。
如图为一颗 3 阶B+树,其中root指向根结点,sqt指向最小关键字结点。

- 查找
定义和图可以知道,两种查找方式,一种是通过 sqt 指针将叶子结点顺序查找。另一种是通过root指针查找方式类似B-但是关键之相同的非终端结点并不结束,而是到叶子结点。 - 插入
B+树的插入仅在叶子结点插入关键字,并在结点关键字根数大于m时将结点分裂为两个结点,同时使得它们的双亲结点分别指向对应结点的最大值。若双亲结点关键字大于m,类推操作。 - 删除
B+树的删除也在叶子结点中进行,若是删除结点是最大值,则其双亲结点中的索引值可作为查找的分界值,不影响结果。若因为操作使得关键字个数小于[ m/2 ],则合并结点,其操作过程类似B-树。




























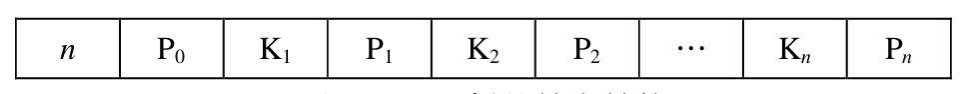

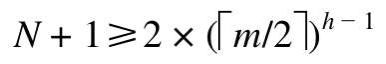
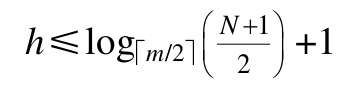
















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








