超大整数的乘法实现---c/c++_c++超大整数相乘-CSDN博客

本文链接：https://blog.csdn.net/qq_44116998/article/details/100847957

本文详细介绍了一种处理大整数乘法的算法，通过将大整数分解为小整数进行计算，采用递归算法实现大整数的拆分与合并。文章提供了具体的算法思想、代码实现及时间复杂度分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言
我们都知道，在在计算机的乘法计算过程中，如果要处理很大的整数，那么计算机硬件是无法表示的，那么，我们就需要考虑将一个大整数分为小整数来进行计算，那么可施行的办法是分解。那么看看如何实现的？

示例
比如计算3278 x 41926,那么我们可以分解为如下式子：
(32 x 10²+ 78) x (419 x 10² + 26);
其中拆开后得到的32 x 419 x 10⁴+ 78可以分解为（3 x 10 + 2 ) x （ 41 x 10 + 9 )x 10⁴ ;
那么我们就可以借助该思想，进行大整数乘法的实现。

算法思想
首先将两个大整数 a ( n 位），b (m 位）进行分解：
因为是一分为二，所以直接表示为a = ah * 10 ^n/2 + al; b = bh * 10^m/2 + bl;
其中h 和 l 分别表示为高位与低位；
那么进行乘法的过程是：
a * b = (ah * 10 ^n/2 + al) * ( bh * 10^m/2 + bl ) = ah * bh *10^(m+n)/2 + ah * bh *10^n/2 + ah * bh *10^m/2 + al *ah;那么很好的进行了大整数的拆分。
在算法的实现过程中，我们可以采取递归算法进行大整数的拆分，很容易想到递归的结束条件就是只有一位数的时候停止执行即可，然后再合并结果。

代码实现

读数时，我们可以采取字符串的形式进行存储。那么在存储之后，我们在转换成数字数组之后，我们最好采取倒序存储数字在数组中，因为我们这样就可以从数组的末尾开始进行数据的分解与整理，更加方便，比如进位时，可以直接在数组末端加进位的值。
再分解时候，进行分半分解，我们可以设置一个函数专门用来将一个n位的数分解为 n / 2的两个数。当然，最好记录分解后的两个数的长度。
现在就是进行求解的过程，将每一部分实现该有的运算过程即可，即按照平时小整数进行运算就解决了。但是，在这个地方进行运算存储的时候，还是采取倒序存储,因为开始进行分解的时候，我们进行的就是倒序分解存储。如图：

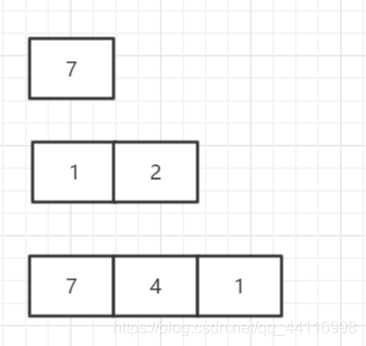
在这里插入图片描述
实际运算时：21 x 7 = 147;

结果相加，在合并输出即可，注意还是倒序输出的模式。

下面图片实际模拟一下过程：
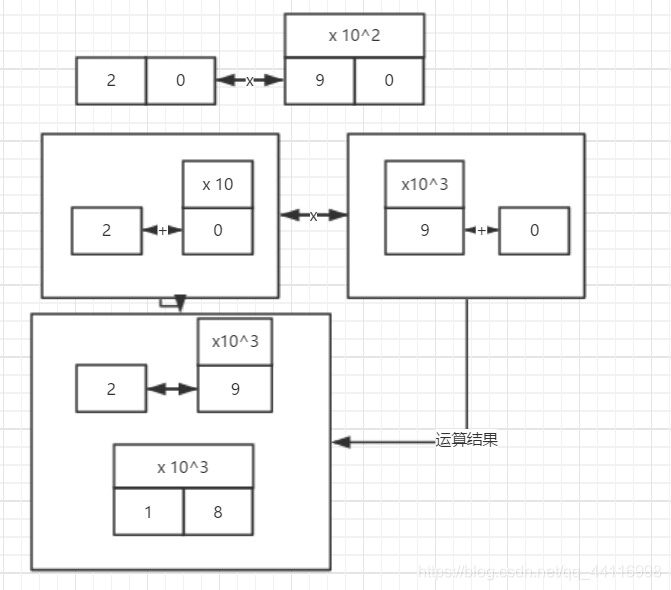
在这里插入图片描述

最后合并过程就很简单了，这而不列举了。

程序代码

#include<stdio.h>
#include<string.h>
#define Maxsize 1000
typedef struct Node{
    int num[Maxsize];//存值 
    int length;//长度
    int exp;//幂 
}Arrynode;
void DepartFunction(Arrynode *prenum,Arrynode *latnum,int start,int length)
{
    int i,j;
    for(i = start,j = 0;i <= start + length - 1;i++,j++)//取length位数 
    {
        latnum->num[j] = prenum->num[i];
    }
    latnum->length = length; //latnum的长度等于取数的长度
    latnum->exp = prenum->exp + start;//la't'nu'm的幂等于开始取数的位置加上prunum的幂 
}
void addFunction(Arrynode *pa,Arrynode *pb,Arrynode *ans)//合并求和运算  
{
    int i,carry,k,palen,pblen,length;
    int ta,tb;
    Arrynode *temp;
    if(pa->exp < pb->exp)//保证a的幂次大于b的幂次 
    {
        temp = pa;
        pa = pb;
        pb = temp;
    }
    ans->exp = pb->exp;//结果的幂为两个数中小的幂
    carry = 0;          //进位初始化为零 
    palen = pa->length + pa->exp;//总长度
    pblen = pb->length + pb->exp;
    if(palen > pblen) //取a b总长度的最大值 
        length = palen;
    else
        length = pblen;
    k = pa->exp - pb->exp;//k为a的左侧需要补充的0的个数 
    for(i = 0;i < length - ans->exp;i++) 
    {
        if(i < k) //a的左侧为零时 
            ta = 0;
        else      //a开始取非零数 
            ta = pa->num[i - k];
        if(i < pb->length)//b中开始取数 
            tb = pb->num[i];
        else        //b取完后补零 
            tb = 0;
        if(i >= pa->length + k)//a先取完补零 
            ta = 0;
        ans->num[i] = (ta + tb + carry) % 10; //个位求和 
        carry = (ta + tb + carry) / 10; 
    }
    if(carry)
        ans->num[i++] = carry;//到计算末尾发现还有进位
    ans->length = i;
}
void multiFunction(Arrynode *pa,Arrynode *pb,Arrynode *ans)
{
    int i,carry,temp;
    int ma = pa->length / 2, mb = pb->length / 2;
    Arrynode ah,al,bh,bl;
    Arrynode t1,t2,t3,t4,current;
    Arrynode *currenttemp;
    if(ma == 0 || mb == 0)//如果其中只有一位数 
    {
        if(ma == 0)//如果a只有一位数 
        {
            currenttemp = pa;
            pa = pb;
            pb = currenttemp;    
        }
        ans->exp = pa->exp + pb->exp; //结果幂次为两者幂次的加和 
        temp = pb->num[0];//因为交换后pb的长度为一，便于记录 
        carry = 0;//进位初始为零
        for(i = 0;i <= pa->length - 1;i++)
        {
            ans->num[i] = (temp * pa->num[i] + carry) % 10;
            carry = (temp*pa->num[i] + carry) / 10;//进位计算    
        }
        if(carry)
            ans->num[i++] = carry;//到计算末尾发现还有进位
        ans->length = i;
        return ; 
    }
    DepartFunction(pa,&ah,ma,pa->length - ma);//数的拆分，a的高位 
    DepartFunction(pa,&al,0,ma); //a的低位 
    DepartFunction(pb,&bh,mb,pb->length - mb); //b的高位 
    DepartFunction(pb,&bl,0,mb); //b的低位 
    multiFunction(&ah,&bh,&t1);//ab的高低位分别求值运算 
    multiFunction(&ah,&bl,&t2);
    multiFunction(&al,&bh,&t3);
    multiFunction(&al,&bl,&t4); 
    addFunction(&t3,&t4,ans);//合并求和运算 
    addFunction(&t2,ans,&current);
    addFunction(&t1,&current,ans);
} 
int main()
{
    Arrynode answer,a,b;
    int i = 0,j = 0;
    char str1[Maxsize];//两个表达式 
    char str2[Maxsize];
    scanf("%s",str1);
    scanf("%s",str2);
    a.length = strlen(str1); //求表达式长度 
    b.length = strlen(str2);
    for(i = a.length - 1;i >= 0;i--)//转化为数字 
        a.num[j++] = str1[i] - '0';
    a.exp = 0; //幂次初始化 
    j = 0;
    for(i = b.length - 1;i >= 0;i--)
        b.num[j++] = str2[i] - '0';
    b.exp = 0; //幂次初始化 
    multiFunction(&a,&b,&answer);//调用两个数相乘函数
    for(i = answer.length - 1;i >= 0;i--) //除去前面为零的多余的数 
        if(answer.num[i] != 0)
            break; 
    for(j = i;j >= 0;j--) 
        printf("%d",answer.num[j]);//输出结果 
    return 0;          
}