题目描述:
某人带了一条狗、一只鸡和一筐菜过河,因船小,每次只能带一样东西过河。若单独留下狗和鸡,则狗会吃鸡;若单独留下鸡和菜,则鸡会吃菜。试问他如何过河?
思路解答:
这个刚开始我尝试运用c++的string+递归来实现该问题,结果发现,陷于了死循环,暂时没有想到修改的好主意,只好用老师给的现成的代码实现了。此处我就发现如何设置一个存储的方式是一个都么重要的事情,老师采用的是两个数组,分别代表河的两岸的物品的情况,并且将数组第一个数num[ 0 ] 设置为存储物品的数量,总共开空间大小为4,即int num[ 4 ],后面三个数字 1 表示存在, 0 表示不存在。后面的事情就好处理了。
- 赋初值
int A[ 4 ] = {3,1,1,1},int B[ 4 ] = {0,0,0,0}; - 确定两个变量 x 和 y,x代表人带过河的物品序号,y代表人带回来的物品序号。
- 循环的判断条件:A[ 0 ] 是否为零,为零时,跳出循环。
- 然后x与y的作用还包括由于遵守规则:刚拿回来的不能再拿离开。
- 危险性的判断:就是两种组合,利用数字表示即可。
代码实现(直接从老师那拿过来,不太好,我加点注释,?)
#include "iostream"
using namespace std;
int Danger( int S[4] )//危险性的判断
{
int d = S[0]*1000+S[1]*100+S[2]*10+S[3];
if ( d == 2110 || d == 2011 ) //鸡和菜,狗和鸡的组合不满足
return 1;
else
return 0;
}
char* Disp( int x )//数字与符号对应转化
{
if ( x == 1 ) return "狗"; else if ( x == 2 ) return "鸡"; else return "菜";
}
void CrossRiver()
{
int A[4] = {3, 1, 1, 1}, B[4] = {0};//初始化,开始都在A边
int i, x, y = 0;
while ( A[0] )//A数量不为零,即未拿完时
{
if ( y ) //刚拿回来的加一
{
A[0]++;
A[y] = 1;
}
A[0]--;//又拿走的减一
x = 0;
i = 1;//每次从一号拿
while ( ! x )
{
while ( ! A[i] || i == y ) //刚拿回来或者已经拿走的
i++;
A[i] = 0;//这次拿走的赋值为零,表示拿走
if ( Danger( A ) )//危险
{
A[i] = 1;//表示不拿目前该物品
i++;//再往后找一个
}
else{//符合拿走的要求时
x = i;
cout << "人带" << Disp( x ) << "过河" << endl << endl;
}
}
B[0]++;//拿到B边时,B边数量加一
B[x] = 1;//拿来的赋值为一,表示存在B边
y = 0 ;
if ( ! A[0] ) break;//A边拿完了
if ( ! Danger( B ) ) //B边不存在冲突项
cout << "人空手回来" << endl << endl;
else
{
i = 1;//从第一个开始查找
while ( ! y )//找到拿走的那一个物品时就退出循环
{
while ( ! B[i] || i == x ) //刚拿来或者已经存在的
i++;
B[0]--;//拿走时,数量减一
B[i] = 0;//表示被拿走
y = i;//拿走的物品编号
cout << "人带" << Disp( y ) << "回来" << endl << endl;
}
}
}
return ;
}
int main()
{
CrossRiver();
return 1;
}实现结果:
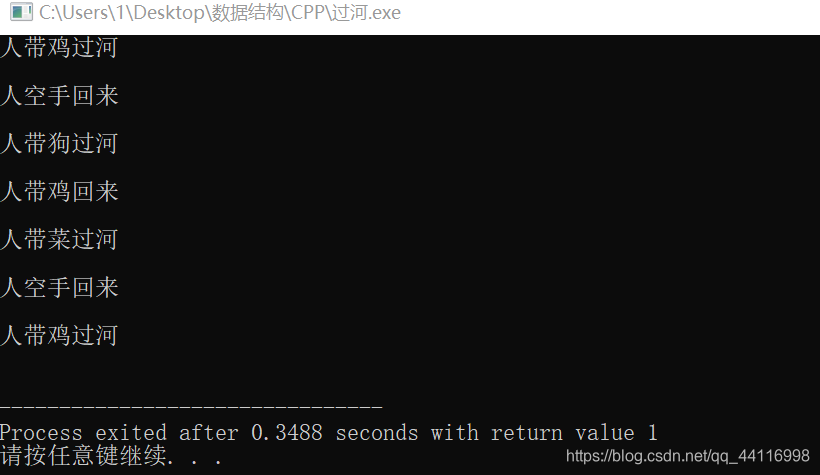








 探讨了使用C++解决经典过河问题的策略,包括如何避免陷入死循环,通过设置存储方式和使用两个数组来表示河两岸的物品状态。详细解析了代码逻辑,包括危险性判断和物品搬运流程。
探讨了使用C++解决经典过河问题的策略,包括如何避免陷入死循环,通过设置存储方式和使用两个数组来表示河两岸的物品状态。详细解析了代码逻辑,包括危险性判断和物品搬运流程。

















 222
222

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








