理解多目标优化问题中的决策空间和目标空间两个核心概念

多目标优化问题中的决策空间和目标空间

决策空间（Decision Space）

定义：决策空间是所有可行解的集合，由决策变量的取值范围和约束条件共同决定。
特点：
维度：维度等于决策变量的数量。例如，若有n个变量，决策空间是n维的。
约束：满足问题所有约束条件（如不等式、等式约束）的变量组合构成可行域。
示例：买手机的时候，决策变量可能包括价格、内存等，其取值范围和约束条件共同形成决策空间。

目标空间（Objective Space）

定义：目标空间是所有可行解通过目标函数映射后的目标值的集合，反映解的质量。
特点：
维度：维度等于目标函数的数量。例如，若有m个目标，目标空间是m维的。
映射关系：每个决策变量组合（决策空间中的点）通过目标函数计算得到目标空间中的点。
示例：若目标是同时最小化价格（f₁）和最大化性能（f₂），目标空间中的点（f₁, f₂）反映不同设计方案的权衡。

两者之间的关系：

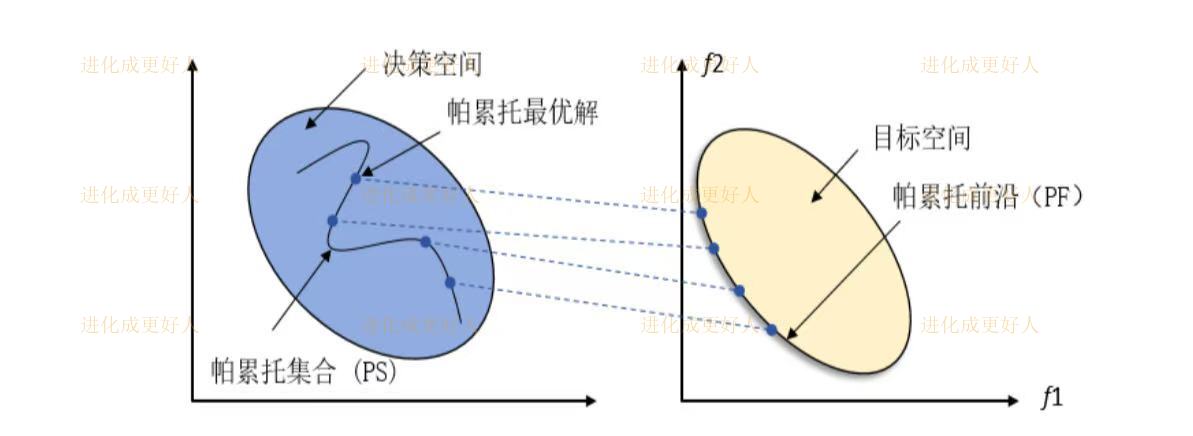
决策空间通过目标函数映射到目标空间。优化过程需在决策空间中搜索，使目标空间中的点逼近帕累托前沿（PF），如图所示。
在决策空间中找到映射到目标空间帕累托前沿的解，实现多目标最优权衡。