卡尔曼滤波通过观测值和估计值求位移、速度、加速度

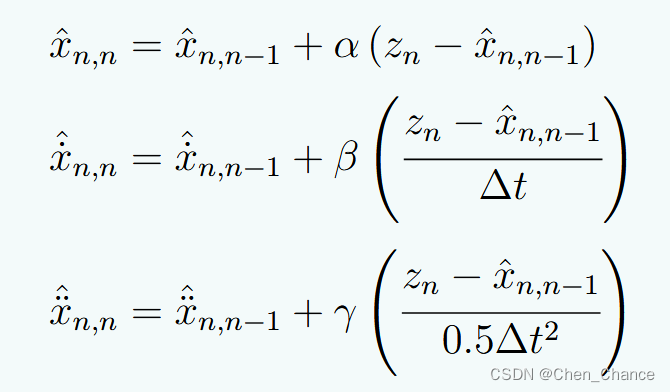
这三个公式描述了动量更新方法,用于优化算法中更新参数的方式。

$${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+\alpha (z_n-{\hat{x}}_{n,n-1})$$

$${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+\beta \left(\frac{z_n-{\hat{x}}_{n,n-1}}{\Delta t}\right)$$

$${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+\gamma \left(\frac{z_n-{\hat{x}}_{n,n-1}}{0.5\Delta t^2}\right)$$

其中:

• ${\hat{x}}_{n,n}$ 表示当前时刻 n 的参数估计值
• ${\hat{x}}_{n,n-1}$ 表示上一时刻 n-1 的参数估计值
• $z_n$ 表示当前时刻 n 的观测值或目标值
• $\alpha$、$\beta$、$\gamma$ 是步长或学习率参数
• $\Delta t$ 表示时间步长

这三个公式分别对应不同的动量更新方式,反映了估计值与观测值之间的差异被纳入更新的不同方式。它们常用于机器学习和优化算法中,用于调整模型参数以最小化损失函数或目标函数。

如何推导得来的

这三个公式实际上是描述了三种不同的动量更新方法,它们都是基于牛顿迭代法的思想推导得到的。

第一个公式是最基本的梯度下降法更新公式:

$${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+\alpha (z_n-{\hat{x}}_{n,n-1})$$

其中 $\alpha$ 是步长,它根据目标函数对参数 $x$ 的梯度进行更新。

第二个公式引入了动量项:

$${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+\beta \left(\frac{z_n-{\hat{x}}_{n,n-1}}{\Delta t}\right)$$

它将目标函数对参数 $x$ 的梯度近似为 $(z_n-{\hat{x}}_{n,n-1})/\Delta t$,即在时间步长 $\Delta t$ 内的变化率。 $\beta$ 是动量系数,通过加入过去的梯度信息来加速收敛。

第三个公式进一步引入了二阶动量项:

$${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+\gamma \left(\frac{z_n-{\hat{x}}_{n,n-1}}{0.5\Delta t^2}\right)$$

它将目标函数对参数 $x$ 的梯度近似为 $(z_n-{\hat{x}}_{n,n-1})/(0.5\Delta t^2)$,即在时间步长 $\Delta t$ 内的加速度变化。 $\gamma$ 是二阶动量系数,通过加入过去的加速度信息来进一步加速收敛。

这些公式的推导思路源自于牛顿迭代法,通过近似目标函数的一阶和二阶导数并结合前一时刻的状态进行参数更新,从而达到加速优化收敛的目的。不同的动量更新方法对应于不同的导数近似方式。

0.5怎么得到的

公式中0.5的存在是为了近似二阶导数。具体来说:

$${\hat{x}}_{n,n}={\hat{x}}_{n,n-1}+\gamma \left(\frac{z_n-{\hat{x}}_{n,n-1}}{0.5\Delta t^2}\right)$$

这个公式试图用 $(z_n-{\hat{x}}_{n,n-1})/(0.5\Delta t^2)$ 来近似目标函数对参数 $x$ 的二阶导数,即加速度。

在数值计算中,常用有限差分法来近似导数。对于一个函数 $f(x)$,它的一阶导数可以用如下方式近似:

$$f^{\prime }(x)\approx \frac{f(x+\Delta x)-f(x)}{\Delta x}$$

而二阶导数可以用如下方式近似:

$$f^{\prime \prime }(x)\approx \frac{f(x+\Delta x)-2f(x)+f(x-\Delta x)}{\Delta x^2}$$

注意到上式分母的 $\Delta x^2$。

将此思路应用到时间域,用 $\Delta t$ 替代 $\Delta x$,就有:

$$\frac{d^{2}x}{d{t}^2}\approx \frac{x(t+\Delta t)-2x(t)+x(t-\Delta t)}{\Delta t^2}$$

进一步化简,我们可以得到:

$$\frac{d^{2}x}{d{t}^2}\approx \frac{x(t+\Delta t)-x(t)}{\Delta t^2/2}$$

所以0.5就是为了对应上面这个二阶导数的近似形式,使得 $(z_n-{\hat{x}}_{n,n-1})/(0.5\Delta t^2)$ 可以近似加速度项。