斜率优化dp

斜率优化

例题1:洛谷P2365 任务安排

我们先使用前缀和的方式,将$t[i]$和$c[i]$​​预处理,$f[i]$表示前面$i$个整好之后的花费,然后得到方程式:
f [ i ] = m i n j = 0 i − 1 { f [ j ] + t [ i ] ∗ ( c [ i ] − c [ j ] ) + s ∗ ( c [ n ] − c [ j ] ) } f[i]=min_{j=0}^{i-1}\{f[j]+t[i]*(c[i]-c[j])+s*(c[n]-c[j]) \} f[i]=minj=0i−1​{f[j]+t[i]∗(c[i]−c[j])+s∗(c[n]−c[j])}
其中$s\ast (c[n]-c[j])$​是费用提前计算的思想,在这里断一下的话,后面都会加上这么多,现在把$min$去掉
$$f[i]=f[j]+t[i]\ast (c[i]-c[j])+s\ast (c[n]-c[j])$$

$$f[j]=f[i]+t[i]\ast (c[j]-c[i])+s\ast (c[j]-c[n])$$

$${\underline{f[j]}}_y={\underline{(t[i]+s)}}_k\ast {\underline{c[j]}}_x+{\underline{(f[i]-s\ast c[n]-t[i]\ast c[i])}}_b$$

整个就可以看成$y=k\ast x+b$​​​,其中$k$​​​是不变的常数,其中$b$​​​越小,$f[i]$​​​​越小,就越好,所以现在就去用$t[i]+s$​去照着图整就完事了,也就是去找第一个​斜率比$t[i]+s$大的那个点,也就是下图蓝色箭头所指的那个

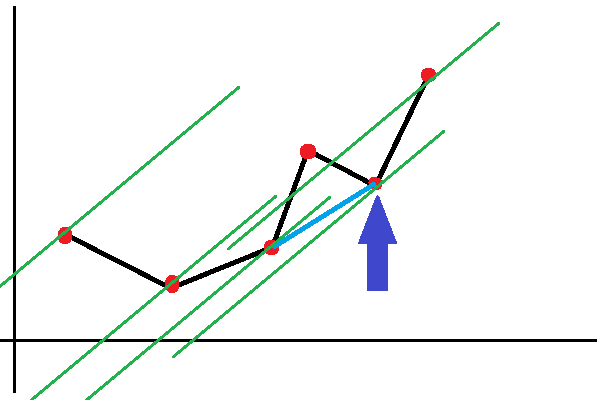
因为我们要$b$越小越好,所以维护一个下凸包,如果是要$b$​​越大越好,就维护一个上凸包,因为$t[i]+s$是单调的,斜率只会越来越大,所以之前匹配的点,也就是斜率小于$t[i]+s$的就可以直接弹掉

• attention 1: 计算斜率的时候可能会遇到分母为$0$的情况,小心哦

#include<cstdio>
#include<algorithm>
#include<cstring>
#define maxn 10000
using namespace std;
int n,s,t[maxn],c[maxn],f[maxn],q[maxn],l,r;
double slope(int x,int y) {return 1.0*(f[y]-f[x])/(c[y]-c[x]==0?(1e-10):(c[y]-c[x]));} 
signed main(){
	scanf("%d %d",&n,&s);
	for(int i=1;i<=n;i++){
		scanf("%d %d",&t[i],&c[i]);
		t[i]+=t[i-1]; c[i]+=c[i-1];
	}
	memset(f,127,sizeof f); f[0]=0;
	for(int i=1;i<=n;i++){
		while(r>l && slope(q[l],q[l+1])<(double)(t[i]+s)) l++;
		f[i]=f[q[l]]+t[i]*(c[i]-c[q[l]])+s*(c[n]-c[q[l]]);
		while(r>l && slope(q[r-1],q[r])>slope(q[r],i)) r--;
		q[++r]=i;
	}
	printf("%d\n",f[n]);
	return 0;
}

---

例题2:洛谷P5017 摆渡车

依然利用前缀和,这道题和上道题同处一辙啊,$dp[i]$​​​​依然表示前面$i$​​​​个的花费,但是有一点不一样的是,同一组的同学等的时间不一样,但是这个也可以用前缀和的形式整出来,如果我们以时间轴来看,就是下面的这个样子,要比以$n$​​​​来看要好得多,所以我们用两个数组$cnt[i]$​​​​表示$i$​​​​点有几个同学,$sum[i]$​​​​​​表示当前这个时间戳的人的时间和,然后现在把他们两个数组以前缀和的形式弄出来,再然后,我们再来思考如何将中间那点人的等待时间表示出来,以中间那段来说,就是$7,9,10$​​​​​的人到$10$​​​​的时间,也就是$i\ast (cnt[i]-cnt[j])-(sum[i]-sum[j])$​​​​​​

d p [ i ] = m i n j = 0 i − 1 { d p [ j ] + i ∗ ( c n t [ i ] − c n t [ j ] ) − ( s u m [ i ] − s u m [ j ] ) } dp[i]=min_{j=0}^{i-1}\{dp[j]+i*(cnt[i]-cnt[j]) -(sum[i]-sum[j]) \} dp[i]=minj=0i−1​{dp[j]+i∗(cnt[i]−cnt[j])−(sum[i]−sum[j])}

$$dp[i]=dp[j]+i\ast cnt[i]-i\ast cnt[j]-sum[i]+sum[j]$$

$${\underline{(dp[j]+sum[j])}}_y={\underline{i}}_k\ast {\underline{cnt[j]}}_x+{\underline{(dp[i]-i\ast cnt[i]+sum[i])}}_b$$

我们是要$dp[i]$​越小越好,所以就是要$b$越小越好,所以是维护下凸包

• attention 1:$slope(q[tail-1],q[tail])$不能写成$slope(q[tail]q,[tail-1])$,假如分母为$0$的话,就会出现什么情况,$slope(q[tail-1],q[tail])$是大于$0$的,$slope(q[tail]q,[tail-1])$是小于$0$​的.

#include<cstdio>
#include<algorithm>
#include<cstring>
#define maxn 4000000
using namespace std;
int n,m,cnt[maxn],sum[maxn],dp[maxn],t,tail,head=1,q[maxn],ans=2147483647;
double slope(int x,int y) {return (double)(sum[y]+dp[y]-sum[x]-dp[x])*1.0/((cnt[y]==cnt[x]?1e-7:cnt[y]-cnt[x]));}
signed main(){
	scanf("%d %d",&n,&m);
	for(int i=1,temp;i<=n;i++){
		 scanf("%d",&temp); t=max(t,temp);
		 cnt[temp]++; sum[temp]+=temp;
	}
	for(int i=1;i<=t+m;i++) cnt[i]+=cnt[i-1],sum[i]+=sum[i-1];
	memset(dp,127,sizeof dp); dp[0]=0;
	for(int i=1;i<=t+m;i++){
		while(tail>head && slope(q[tail-1],q[tail])>slope(q[tail],i-m)) tail--;
		if(i-m>=0) q[++tail]=i-m;
		while(tail>head && slope(q[head],q[head+1])<=(double)i) head++;
		dp[i]=cnt[i]*i-sum[i];
		if(i-m>=0) dp[i]=min(dp[q[head]]+i*(cnt[i]-cnt[q[head]])-sum[i]+sum[q[head]],dp[i]);
	}
	for(int i=t;i<=t+m;i++) ans=min(ans,dp[i]);
	printf("%d\n",ans);
	return 0;
}

---

总结

• 将$dp$转移方程先写出来,然后再进行拆分组合,核心就是找到只有$j$的,其他的都没啥关系,和$i$有关系的一般都是常数或者定值,就没关系,随便放.
• 斜率计算的小细节要注意:分母不为$0$​,除的时候注意顺序
• 一些技巧经常和这个一起用,如前缀和,费用提前计算之类的

---

因为是学习笔记,有什么问题还请指正,如果有哪里写漏了也欢迎指出.
点赞+关注😍