数论之同余与逆元

数论之同余与逆元

• 同余
  两个整数a, b和一个整数m，如果a除以m所得的余数和b除以m所得的余数相等，即
  
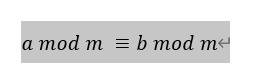
  称为a和b对m同余，m称为同余的模。
  同余的符号记为：
  

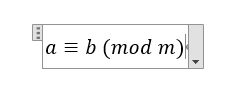
• 一元线性同余方程
  
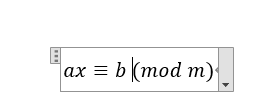
  此式子的含义是ax除以m，b除以m，两者的余数相同。
  求解x的值。
  上面的式子也可以理解为ax-b是m的整数倍。设y是倍数，那么ax - b = my;
  移项可得ax - my = b。因为y可以为负数，则我们改写为ax + my = b；
  这上面的式子就是扩展欧几里得中得二元一次不定方程。
  当且仅当gcd(a, m)能整除b的时候有整数解。
  当满足gcd(a, m) = b的时候，我们可以直接用扩展欧几里得求解得到x;
  不满足gcd(a, m) = b的时候我们需要结合逆元来处理问题

• 逆元

• 扩展欧几里得方法求解逆元

给出a和m，求解方程

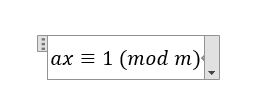
即ax除以m的余数是1

上式有解的条件是gcd(a, m) = 1，即a，m互素。
该问题等价于求解ax + my = 1（就可以用扩展欧几里得求解）

方程ax≡1 (mod m)的一个解x,称x为a模m的逆

求逆元的代码：

void exgcd(int a, int b, int &x, int &y)
{
	if (!b)
	{
		x = 1;
		y = 0;
		return ;
	}
	exgcd(b, a % b, x, y);
	int t = x;
	x = y;
	y = t - (a / b) * y;
}

int inv(int a, int m)
{
	int x, y;
	exgcd(a, m, x, y);
	return (m + x % m) % m; //x可能为负数，处理一下 
}

上面是用扩展欧几里得的算法求解的逆元

下面说一下用费马小定理的方法求解逆元

• 费马小定理求解逆元
  如果模的数字m为素数时，我们可以使用费马小定理求解
  
  则我们就可以直接用快速幂来求解逆元了。

使用费马小定理求解逆元的代码部分：

ll npow(ll a, ll n)
{
	ll res = 1;
	while (n)
	{
		if (n & 1)
		{
			res = res * a % mod;//这里的mod就是下面的mod 
		}
		a = a * a % mod;
		b >>= 1; 
	}
	return res;
}

ll inv(ll a, ll mod)
{
	return npow(a, mod - 2);
}

• 公式求解逆元（逆元打表 ）
  有些时候当mod为素数，并且要求我们求解1~n的所有逆时，我们有一个O(N)复杂度的方法求解逆元。
  递推公式:
  
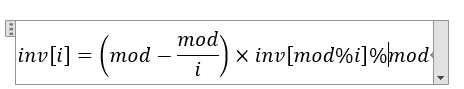
  证明如下：
  
  边界条件:
  inv[1] = 1;

• 逆元与除法取模

逆元的一个重要运用是求除法的模。
比如求（a / b) mod m，即a除以b，然后对m取模。可能这里的a, b都是很大的数字，做除法后再取模会损失精度。我们可以用逆元的方法避免除法：

设b的逆元是k，则有：