面试经典算法16 - 从前序与中序遍历序列构造二叉树
LeetCode.105
公众号:阿Q技术站
问题描述
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
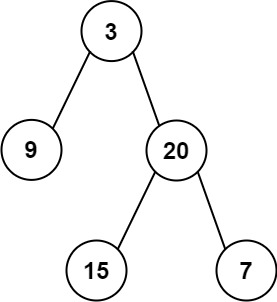
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
思路
递归
构造二叉树的基本思路是利用先序遍历和中序遍历的特点。先序遍历的顺序是根节点、左子树、右子树;中序遍历的顺序是左子树、根节点、右子树。
- 首先,先序遍历的第一个元素一定是根节点的值。
- 然后,在中序遍历中找到这个根节点的位置,它左边的元素都是左子树的节点,右边的元素都是右子树的节点。
- 根据中序遍历中根节点的位置,可以得到左子树和右子树的节点数目,进而可以在先序遍历中找到左子树和右子树的分界点。
- 递归地构建左子树和右子树。
非递归
-
创建根节点并将其压入栈中。
-
初始化前序遍历索引
preIndex为 0,表示当前处理的是前序遍历的第一个元素(根节点)。 -
循环执行以下步骤,直到栈为空:
a. 从栈中弹出一个节点作为当前节点。
b. 如果当前节点的值不等于中序遍历中的当前值(由
inIndex指示),则将当前节点的右子节点设置为前序遍历中的下一个值,并将右子节点压入栈中。c. 否则,更新
inIndex指示下一个中序遍历的值,并将当前节点的左子节点设置为前序遍历中的下一个值,然后将左子节点压入栈中。 -
返回根节点。
图解
今天给大家画一个相对简单好理解的流程图。
3
/ \
9 20
/ \
15 7
preorder: [3, 9, 20, 15, 7]
inorder: [9, 3, 15, 20, 7]
1. 创建根节点 root = TreeNode(3)
2. 将 root 压入栈 s 中
3. preIndex = 1, inIndex = 0
4. 进入循环,preIndex < preorder.size()
- currNode = s.top() = root
- root->val != inorder[0] (9)
- root->left = TreeNode(9)
- 将 root->left 压入栈 s 中
- preIndex = 2
5. preIndex = 2, inIndex = 0
6. 进入循环,preIndex < preorder.size()
- currNode = s.top() = root->left (9)
- root->left->val != inorder[1] (3)
- root->left->left = TreeNode(20)
- 将 root->left->left 压入栈 s 中
- preIndex = 3
7. preIndex = 3, inIndex = 0
8. 进入循环,preIndex < preorder.size()
- currNode = s.top() = root->left->left (20)
- root->left->left->val != inorder[2] (15)
- root->left->left->left = TreeNode(15)
- 将 root->left->left->left 压入栈 s 中
- preIndex = 4
9. preIndex = 4, inIndex = 0
10. 进入循环,preIndex < preorder.size()
- currNode = s.top() = root->left->left->left (15)
- root->left->left->left->val != inorder[3] (20)
- root->left->left->left->right = TreeNode(7)
- 将 root->left->left->left->right 压入栈 s 中
- preIndex = 5
11. preIndex = 5, inIndex = 0
12. 进入循环,preIndex < preorder.size()
- preIndex == preorder.size(),跳出循环
13. 返回根节点 root
参考代码
C++
递归
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
unordered_map<int, int> index_map; // 用于存储中序遍历中节点值和索引的映射
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
// 构建中序遍历中节点值和索引的映射
for (int i = 0; i < inorder.size(); ++i) {
index_map[inorder[i]] = i;
}
return build(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
}
TreeNode* build(vector<int>& preorder, vector<int>& inorder, int pre_left, int pre_right, int in_left, int in_right) {
if (pre_left > pre_right || in_left > in_right) {
return nullptr; // 如果前序遍历或中序遍历的起始位置大于结束位置,返回空节点
}
int root_val = preorder[pre_left]; // 当前子树的根节点值
TreeNode* root = new TreeNode(root_val); // 创建当前子树的根节点
// 在中序遍历中找到根节点的位置
int index = index_map[root_val];
int left_size = index - in_left; // 左子树的节点数目
// 递归构建左子树和右子树
root->left = build(preorder, inorder, pre_left + 1, pre_left + left_size, in_left, index - 1);
root->right = build(preorder, inorder, pre_left + left_size + 1, pre_right, index + 1, in_right);
return root; // 返回当前子树的根节点
}
};
// 打印二叉树的先序遍历结果
void printPreorder(TreeNode* root) {
if (!root) {
return;
}
cout << root->val << " ";
printPreorder(root->left);
printPreorder(root->right);
}
int main() {
vector<int> preorder = {3, 9, 20, 15, 7}; // 二叉树的先序遍历序列
vector<int> inorder = {9, 3, 15, 20, 7}; // 二叉树的中序遍历序列
Solution solution;
TreeNode* root = solution.buildTree(preorder, inorder); // 构建二叉树
printPreorder(root); // 输出二叉树的先序遍历结果
cout << endl;
return 0;
}
非递归
#include <iostream>
#include <vector>
#include <stack>
#include <unordered_map>
using namespace std;
// 二叉树节点的定义
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (preorder.empty()) {
return nullptr; // 如果前序遍历序列为空,返回空指针
}
TreeNode* root = new TreeNode(preorder[0]); // 创建根节点
stack<TreeNode*> s; // 辅助栈,用于模拟递归过程
s.push(root); // 将根节点压入栈中
int preIndex = 1; // 前序遍历索引,从第二个元素开始
int inIndex = 0; // 中序遍历索引,从第一个元素开始
while (preIndex < preorder.size()) {
TreeNode* currNode = s.top(); // 获取栈顶节点作为当前节点
if (currNode->val != inorder[inIndex]) {
// 如果当前节点的值不等于中序遍历中的当前值,说明还有左子树需要处理
currNode->left = new TreeNode(preorder[preIndex++]); // 创建左子节点
s.push(currNode->left); // 将左子节点压入栈中
} else {
// 如果当前节点的值等于中序遍历中的当前值,说明当前节点是中序遍历的根节点
while (!s.empty() && s.top()->val == inorder[inIndex]) {
// 依次弹出栈顶节点,直到栈为空或栈顶节点的值不等于中序遍历的当前值
currNode = s.top();
s.pop();
++inIndex; // 更新中序遍历索引,指向下一个节点
}
currNode->right = new TreeNode(preorder[preIndex++]); // 创建右子节点
s.push(currNode->right); // 将右子节点压入栈中
}
}
return root; // 返回根节点
}
};
// 打印二叉树的先序遍历结果
void printPreorder(TreeNode* root) {
if (!root) {
return;
}
cout << root->val << " ";
printPreorder(root->left);
printPreorder(root->right);
}
int main() {
vector<int> preorder = {3, 9, 20, 15, 7}; // 二叉树的先序遍历序列
vector<int> inorder = {9, 3, 15, 20, 7}; // 二叉树的中序遍历序列
Solution solution;
TreeNode* root = solution.buildTree(preorder, inorder); // 构建二叉树
printPreorder(root); // 输出二叉树的先序遍历结果
cout << endl;
return 0;
}
Java
import java.util.HashMap;
import java.util.Map;
import java.util.Stack;
// 二叉树节点的定义
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder.length == 0) {
return null; // 如果前序遍历序列为空,返回空节点
}
TreeNode root = new TreeNode(preorder[0]); // 创建根节点
Stack<TreeNode> stack = new Stack<>(); // 辅助栈,用于模拟递归过程
stack.push(root); // 将根节点压入栈中
int preIndex = 1; // 前序遍历索引,从第二个元素开始
int inIndex = 0; // 中序遍历索引,从第一个元素开始
while (preIndex < preorder.length) {
TreeNode currNode = stack.peek(); // 获取栈顶节点作为当前节点
if (currNode.val != inorder[inIndex]) {
// 如果当前节点的值不等于中序遍历中的当前值,说明还有左子树需要处理
currNode.left = new TreeNode(preorder[preIndex++]); // 创建左子节点
stack.push(currNode.left); // 将左子节点压入栈中
} else {
// 如果当前节点的值等于中序遍历中的当前值,说明当前节点是中序遍历的根节点
while (!stack.isEmpty() && stack.peek().val == inorder[inIndex]) {
// 依次弹出栈顶节点,直到栈为空或栈顶节点的值不等于中序遍历的当前值
currNode = stack.pop();
inIndex++; // 更新中序遍历索引,指向下一个节点
}
currNode.right = new TreeNode(preorder[preIndex++]); // 创建右子节点
stack.push(currNode.right); // 将右子节点压入栈中
}
}
return root; // 返回根节点
}
}
public class Main {
public static void main(String[] args) {
int[] preorder = {3, 9, 20, 15, 7}; // 二叉树的先序遍历序列
int[] inorder = {9, 3, 15, 20, 7}; // 二叉树的中序遍历序列
Solution solution = new Solution();
TreeNode root = solution.buildTree(preorder, inorder); // 构建二叉树
printPreorder(root); // 输出二叉树的先序遍历结果
System.out.println();
}
private static void printPreorder(TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " ");
printPreorder(root.left);
printPreorder(root.right);
}
}
Python
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
if not preorder:
return None
root = TreeNode(preorder[0]) # 创建根节点
stack = [root] # 辅助栈,用于模拟递归过程
preIndex, inIndex = 1, 0 # 前序遍历索引从第二个元素开始,中序遍历索引从第一个元素开始
while preIndex < len(preorder):
currNode = stack[-1] # 获取栈顶节点作为当前节点
if currNode.val != inorder[inIndex]:
# 如果当前节点的值不等于中序遍历中的当前值,说明还有左子树需要处理
currNode.left = TreeNode(preorder[preIndex]) # 创建左子节点
stack.append(currNode.left) # 将左子节点压入栈中
preIndex += 1 # 更新前序遍历索引
else:
# 如果当前节点的值等于中序遍历中的当前值,说明当前节点是中序遍历的根节点
while stack and stack[-1].val == inorder[inIndex]:
# 依次弹出栈顶节点,直到栈为空或栈顶节点的值不等于中序遍历的当前值
currNode = stack.pop()
inIndex += 1 # 更新中序遍历索引
currNode.right = TreeNode(preorder[preIndex]) # 创建右子节点
stack.append(currNode.right) # 将右子节点压入栈中
preIndex += 1 # 更新前序遍历索引
return root # 返回根节点























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








