剑指offer刷题笔记

最新推荐文章于 2024-11-03 21:27:26 发布
最新推荐文章于 2024-11-03 21:27:26 发布
阅读量177 收藏
点赞数
文章标签： 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_44678607/article/details/131668153
版权

剑指offer刷题笔记

09. 用两个栈实现队列

题目：用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 ：

输入：
["CQueue","appendTail","deleteHead","deleteHead","deleteHead"]
[[],[3],[],[],[]]
输出：[null,null,3,-1,-1]

思路：

当栈 outStack不为空： outStack中仍有已完成倒序的元素，因此直接返回 outStack的栈顶元素。
否则，当 inStack为空： 即两个栈都为空，无元素，因此返回 -1 。
否则： 将栈 inStack元素全部转移至栈 outStack中，实现元素倒序，并返回栈 outStack的栈顶元素。

代码：

class CQueue {
    private Stack<Integer> inStack,outStack;
    public CQueue() {
        inStack = new Stack<Integer>();
        outStack = new Stack<Integer>();
    }
    
    public void appendTail(int value) {
        inStack.add(value);
    }
    
    public int deleteHead() {
        if(!outStack.empty()){
            return outStack.pop();
        }
        if(inStack.empty()){
            return -1;
        }
        while(!inStack.empty()){
            outStack.push(inStack.pop());
        }
        return outStack.pop();
    }
}

思路二：

将一个栈当作输入栈，用于压入appendTail 传入的数据；另一个栈当作输出栈，用于 deleteHead 操作。

每次deleteHead 时，若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈，这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。

代码二：

class CQueue {
    private Stack<Integer> inStack,outStack;
    public CQueue() {
        inStack = new Stack<Integer>();
        outStack = new Stack<Integer>();
    }
    
    public void appendTail(int value) {
        inStack.add(value);
    }
    
    public int deleteHead() {
        if(outStack.isEmpty()){
            if(inStack.isEmpty()) return -1;
            while(!inStack.isEmpty()){
                outStack.push(inStack.pop());
            }
        }
        return outStack.pop();
    }
}

30. 包含min函数的栈

题目：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.min();   --> 返回 -2.

思路：

对于栈来说，如果一个元素 a 在入栈时，栈里有其它的元素 b, c, d，那么无论这个栈在之后经历了什么操作，只要 a 在栈中，b, c, d 就一定在栈中，因为在 a 被弹出之前，b, c, d 不会被弹出。

因此，在操作过程中的任意一个时刻，只要栈顶的元素是 a，那么我们就可以确定栈里面现在的元素一定是 a, b, c, d。

那么，我们可以在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时，如果栈顶元素是 a，我们就可以直接返回存储的最小值 m。

代码：

class MinStack {

    private Stack<Integer> stack;
    private Stack<Integer> minStack;

    /** initialize your data structure here. */
    public MinStack() {
        stack = new Stack<Integer>();
        minStack = new Stack<Integer>();
        minStack.push(Integer.MAX_VALUE);
    }
    
    public void push(int x) {
        stack.push(x);
        minStack.push(Math.min(minStack.peek(), x));   
    }
    
    public void pop() {
        stack.pop(); 
        minStack.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int min() {
        return minStack.peek();
    }
}

06. 从尾到头打印链表

输入一个链表的头节点，从尾到头反过来返回每个节点的值（用数组返回）。

示例 ：

输入：head = [1,3,2]
输出：[2,3,1]

**思路一：**遍历链表，反向放入数组

首先，通过getLength函数获取到链表的元素个数size，其次，通过遍历链表将链表中的元素值反向放入提前创好的数组res中，再将res返回。

代码一：

class Solution {
    public int[] reversePrint(ListNode head) {
        ListNode tmp = head;
        int size = getLength(head);
        int[] res = new int[size];

        while(tmp != null){
            res[--size] = tmp.val;
            tmp = tmp.next;
        }
        return res;
    }

    public int getLength(ListNode head){
        int size = 0;
        if(head == null){
            return 0;
        }
        size++;
        while(head.next != null){
            size++;
            head = head.next;
        }
        return size;
    }

}

**思路二：**利用栈先入后出的特点

使用栈将链表元素顺序倒置。从链表的头节点开始，依次将每个节点压入栈内，然后依次弹出栈内的元素并存储到数组中。

代码二：

class Solution {
    public int[] reversePrint(ListNode head) {
        Stack<ListNode> stack = new Stack<ListNode>();
        ListNode temp = head;
        while(temp != null){
            stack.push(temp);
            temp = temp.next;
        }

        int size = stack.size();
        int res[] = new int[size];

        for(int i=0;i < size;i++){
            res[i] = stack.pop().val;
        }     
        return res;
    }
}

**思路三：**利用递归的方法

利用递归法将链表中的元素值反向放入一个list集合，然后通过遍历list集合将元素值放入res数组中。

代码三：

class Solution {
    List<Integer> tmp = new ArrayList<Integer>();
    public int[] reversePrint(ListNode head) {
        recur(head);
        int size = tmp.size();
        int res[] = new int[size];
        for(int i=0;i < size;i++){
            res[i] = tmp.get(i);
        }
        return res;
    }

    public void recur(ListNode head){
        if(head == null) return;
        recur(head.next);
        tmp.add(head.val);
    }
}

24. 反转链表

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

思路一：

假设链表为 1 →2→3→∅，我们想要把它改成 ∅←1←2←3。

在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

**代码一：**双链表

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null;
        ListNode curr = head;

        while(curr != null){
            ListNode next = curr.next;
            curr.next = pre;
            pre = curr;
            curr = next;
        }
        return pre;
    }
}

图解：

image-20230321213034157

**思路二：**使用栈的先入后出特性

将链表节点全部摘掉放入栈中/先得到反转后的头节点，再栈中的节点全部出栈，然后重新连成一个新的链表，最后一个节点就是反转前的头节点，一定要让他的next为空，否则会构成环。

代码二：

class Solution {
    public ListNode reverseList(ListNode head) {
        Stack<ListNode> stack = new Stack<ListNode>();
        ListNode temp = head;

        //将链表的节点全部压入栈
        while(temp != null){
            stack.push(temp);
            temp = temp.next;
        }

        //如果链表中没有元素，说明链表为空
        if(stack.isEmpty()) return null;

        //取出栈顶的元素作为新链表的头节点
        ListNode node = stack.pop();
        ListNode newHead = node;

        while(!stack.isEmpty()){
            ListNode tempNode = stack.pop();
            node.next = tempNode;
            node = node.next;
        }

        //最后一个节点就是反转前的头节点，一定要让他的next为空，否则会构成环
        node.next = null;
        return newHead;
    }
}

**思路三：**递归法

代码三:

class Solution {
    public ListNode reverseList(ListNode head) {
        //终止条件
        if(head == null || head.next == null){
            return head;
        }
        //保存当前节点的下一个节点
        ListNode next = head.next;
        //从当前节点的下一个节点开始递归调用
        ListNode reverse = ReverseList(next);
        //reverse是反转之后的链表，因为函数reverseList表示的是对链表的反转
        //所以反转完之后next肯定是链表reverse的尾结点，然后我们再把当前节点
        //head挂到next节点的后面就完成了链表的反转。
        next.next = head;
        head.next = null;
        return reverse;
    }
}

图解：

image-20230321215534003

05. 替换空格

请实现一个函数，把字符串 s 中的每个空格替换成"%20"。

示例 ：

输入：s = "We are happy."
输出："We%20are%20happy."

**思路一：**使用StringBuilder

初始化一个StringBuilder ，记为 sb ；
遍历列表 s 中的每个字符 c ：
当 c 为空格时：向 sb 后添加字符串 “%20” ；
当 c 不为空格时：向 sb 后添加字符 c ；
将列表 sb 转化为字符串并返回。

代码一：

class Solution {
    public String replaceSpace(String s) {
        StringBuilder sb = new StringBuilder();

        int len = s.length();
        for(int i = 0;i < len;i++){
            char c = s.charAt(i);
            if(c == ' '){
                sb.append("%20");
            } else {
                sb.append(c);
            }
        }

        return sb.toString();
    }
}

思路二：

创建一个字符数组array，长度为字符串长度的3倍，通过String的charAt()方法，遍历字符串的每个字符，通过判断字符是否为空格，如果为空格，就将'%'、'2'、'0'替换掉空格，如果不是空格，就不变。然后通过String的有参构造，将array作为参数构造出一个新字符串，并返回。

代码二：

class Solution {
    public String replaceSpace(String s) {
        int length = s.length();
        char[] array = new char[length * 3];
        int size = 0;
        for (int i = 0; i < length; i++) {
            char c = s.charAt(i);
            if (c == ' ') {
                array[size++] = '%';
                array[size++] = '2';
                array[size++] = '0';
            } else {
                array[size++] = c;
            }
        }
        String newStr = new String(array, 0, size);
        return newStr;
    }
}

31. 栈的压入、弹出序列

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

示例 1：

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

示例 2：

输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false
解释：1 不能在 2 之前弹出。

**思路：**栈模拟

可以遍历这两个数组，模拟入栈和出栈操作，判断两个数组是否为有效的栈操作序列。

先遍历pushed数组，将pushed数组的元素依次压入栈，当每次压入栈后，先循环判断stack的栈顶元素是否等于popped数组的当前元素，如果符合，就将当前stack的栈顶元素弹出，然后判断popped数组的下一个元素，直到遍历完pushed数组，判断stack中是否为空，如果为空，则说明出栈顺序正确，否则就不正确。

代码：

class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        Deque<Integer> stack = new ArrayDeque<Integer>();
        int n = pushed.length;
        for(int i = 0,j = 0;i < n;i++){
            stack.push(pushed[i]);
            while(!stack.isEmpty() && stack.peek() == popped[j]){
                stack.pop();
                j++;
            }
        }
        return stack.isEmpty();
    }
}

35.复杂链表的复制

题目：

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

示例 ：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-q3iHnjKn-1689076808092)(C:\Users\10044\AppData\Roaming\Typora\typora-user-images\image-20230331211757176.png)]

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

思路一：哈希表

首先，先创建一个HashMap集合，然后遍历一次链表，在遍历过程中，将原链表当前节点作为key值，新创建一个val值与当前节点值相同的节点作为value值，当遍历完第一遍后，便实现原节点->新节点的Map映射。

其次，再次遍历该链表，构建新链表的next和random指向。

代码：

class Solution {
    public Node copyRandomList(Node head) {
        if(head == null) return null;
        Node cur = head;
        Map<Node, Node> map = new HashMap<>();
        // 3. 复制各节点，并建立 “原节点 -> 新节点” 的 Map 映射
        while(cur != null) {
            map.put(cur, new Node(cur.val));
            cur = cur.next;
        }
        cur = head;
        // 4. 构建新链表的 next 和 random 指向
        while(cur != null) {
            map.get(cur).next = map.get(cur.next);
            map.get(cur).random = map.get(cur.random);
            cur = cur.next;
        }
        // 5. 返回新链表的头节点
        return map.get(head);
    }
}

思路二：拼接+拆分

先遍历原链表，复制各节点，构建拼接链表。

image-20230331221208389

然后构建新链表各节点的 random 指向：当访问原节点 cur 的随机指向节点 cur.random 时，对应新节点 cur.next 的随机指向节点为 cur.random.next 。

拆分原 / 新链表：设置 pre / cur 分别指向原 / 新链表头节点，遍历执行 pre.next = pre.next.next 和 cur.next = cur.next.next 将两链表拆分开。

最后，返回新链表的头节点 res 即可。

代码：

class Solution {
    public Node copyRandomList(Node head) {
        if(head == null) return null;
        //1.复制各个节点，拼接成新链表
        Node cur = head;

        while(cur != null){
            Node tmp = new Node(cur.val);
            tmp.next = cur.next;
            cur.next = tmp;
            cur = tmp.next;
        }

        //2.构建新节点的random指向
        cur = head;
        while(cur != null) {
            if(cur.random != null){
                cur.next.random = cur.random.next;
            }             
            cur = cur.next.next;
        }

        //3.拆分成两个链表
        cur = head.next;
        Node pre = head, res = head.next;//res为新链表头结点
        while(cur.next != null){
            pre.next = pre.next.next;
            cur.next = cur.next.next;
            pre = pre.next;
            cur = cur.next;
        }
        pre.next = null;
        return res;     
    }
}

58 - II. 左旋转字符串

题目：

字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如，输入字符串"abcdefg"和数字2，该函数将返回左旋转两位得到的结果"cdefgab"。

示例 1：

输入: s = "abcdefg", k = 2
输出: "cdefgab"

示例 2：

输入: s = "lrloseumgh", k = 6
输出: "umghlrlose"

思路一：列表遍历拼接

新建一个StringBuilder，记为sb ；
先向 sb 添加 “第 n + 1 位至末位的字符” ；
再向sb 添加 “首位至第 n 位的字符” ；
将 sb 转化为字符串并返回。

代码一：

class Solution {
    public String reverseLeftWords(String s, int n) {
        StringBuilder sb = new StringBuilder();
        for(int i = n; i < s.length(); i++){
            sb.append(s.charAt(i));
        }
        for(int i = 0; i < n; i++){
            sb.append(s.charAt(i));
        }
        return sb.toString();
    }
}

利用求余运算优化代码：

class Solution {
    public String reverseLeftWords(String s, int n) {
        StringBuilder sb = new StringBuilder();
        for(int i = n; i < n + s.length(); i++){
            sb.append(s.charAt(i % s.length()));
        }
        return sb.toString();
    }
}

**思路二：**字符串切片

代码二：

class Solution {
    public String reverseLeftWords(String s, int n) {
        return s.substring(n,s.length()) + s.substring(0,n);
    }
}

03. 数组中重复的数字

题目：

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3

**思路一：**HashSet

初始化： 新建 HashSet ，记为 dic ；
遍历数组 nums 中的每个数字 num ：
当 num 在 dic中，说明重复，直接返回 num；
将 num 添加至 dic 中；
如果不存在重复数字，就返回 -1。

代码一：

class Solution {
    public int findRepeatNumber(int[] nums) {
        Set<Integer> dic = new HashSet<Integer>();
        for(int num: nums){
            if(dic.contains(num)) return num;
            dic.add(num);
        }
        return -1;
    }
}

思路二：原地交换

遍历数组 nums ，设索引初始值为 i = 0:

若 nums[i] = i： 说明此数字已在对应索引位置，无需交换，因此跳过；
若 nums[nums[i]] = nums[i] ： 代表索引 nums[i]处和索引 i处的元素值都为 nums[i] ，即找到一组重复值，返回此值 nums[i]；
否则： 交换索引为 i 和 nums[i]的元素值，将此数字交换至对应索引位置。
若遍历完毕尚未返回，则返回 -1 。

class Solution {
    public int findRepeatNumber(int[] nums) {
        int i = 0;
        while(i < nums.length){
            if(nums[i] == i){
                i++;
                continue;
            }
            if(nums[nums[i]] == nums[i]) return nums[i];
            int tmp = nums[i];//将当前遍历位置的值赋给tmp
            nums[i] = nums[tmp];//将当前值对应索引位置的值赋到当前遍历位置
            nums[tmp] = tmp;//将当前遍历位置的值赋给当前值对应索引位置
        }
        return -1;
    }
}

53 - I. 在排序数组中查找数字 I

题目:

统计一个数字在排序数组中出现的次数。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

**思路一：**暴力法

代码一：

class Solution {
    public int search(int[] nums, int target) {
        int count = 0;
        for(int i = 0; i < nums.length; i++){
            if(nums[i] == target){
                count++;
            }
        }
        return count;
    }
}

**思路二：**二分法

  1. 初始化 i = 0 j = nums.length - 1

  2. 循环二分，当闭区间 [i, j] 无元素时跳出（i > j）

    1. 计算中点 m = (i+j)/2
    2. 若nums[m] < target,则target在闭区间 [m + 1, j]中，因此执行i = m + 1
    3. 若 nums[m] > target，则 target 在闭区间 [i, m - 1] 中，因此执行 j = m - 1；
    4. 若 nums[m] = target ，则右边界 right 在闭区间 [m+1, j] 中；左边界 left在闭区间 [i, m-1] 中。因此分为以下两种情况：
      1. 若查找 右边界 right ，则执行 i = m + 1 ；（跳出时 i 指向右边界）
      2. 若查找 左边界 left ，则执行 j = m - 1 ；（跳出时 j 指向左边界）

  3. 应用两次二分，分别查找 right 和 left ，最终返回 right - left - 1 即可。

代码二：

class Solution {
    public int search(int[] nums, int target) {
        int i = 0, j = nums.length - 1;
        while(i <= j){
            int m = (i + j)/2;
            if(nums[m] <= target) i = m + 1;
            else j = m - 1;
        }
        int right = i;

        //若数组中无 target ，则提前返回
        if(j >= 0 && nums[j] != target) return 0;

        i = 0; j = nums.length - 1;
        while(i <= j){
            int m = (i + j)/2;
            if(nums[m] < target) i = m + 1;
            else j = m - 1;
        }
        int left = j;

        return right - left - 1;
    }
}

为简化代码，可将二分查找右边界right的代码封装至函数 helper() 。

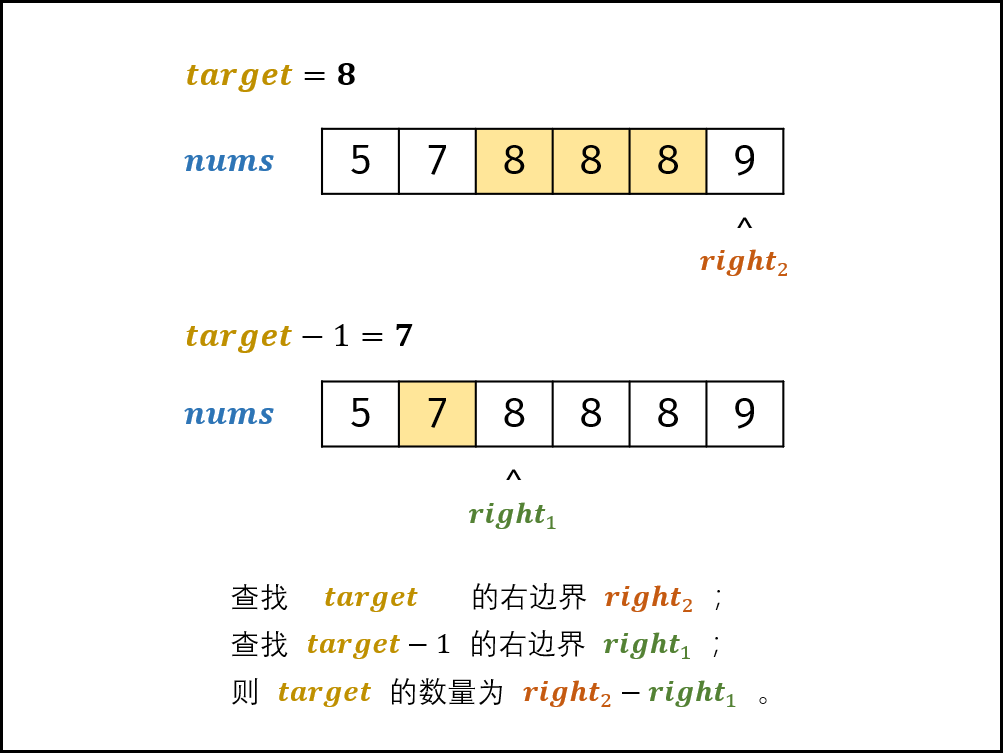
Picture2.png

由于数组 nums 中元素都为整数，因此可以分别二分查找 target 和 target - 1的右边界，将两结果相减并返回即可。

代码三：

class Solution {
    public int search(int[] nums, int target) {
        return helper(nums, target) - helper(nums, target - 1);
    }

    //查找右边界的函数
    int helper(int[] nums, int tar) {
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= tar) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
}

53 - II. 0～n-1中缺失的数字

题目：

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

示例 1:

输入: [0,1,3]
输出: 2

示例 2:

输入: [0,1,2,3,4,5,6,7,9]
输出: 8

**思路：**二分法

排序数组中的搜索问题，首先想到二分法解决。
根据题意，数组可以按照以下规则划分为两部分。

  • 左子数组： nums[i] = i；
  • 右子数组：nums[i] != i；

缺失的数字等于 “右子数组的首位元素” 对应的索引；因此考虑使用二分法查找 “右子数组的首位元素” 。

代码：

class Solution {
    public int missingNumber(int[] nums) {
        int i = 0, j = nums.length - 1;
        while(i <= j){
            int m = (i + j)/2;
            if(nums[m] == m) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
}

04. 二维数组中的查找

题目：

在一个 n * m 的二维数组中，每一行都按照从左到右 非递减 的顺序排序，每一列都按照从上到下 非递减 的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

思路一：直接遍历

思路二：二分查找

对二维数组的每一行一维数组进行二分查找。

代码二：

class Solution {
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        int n = matrix.length;//行数

        for(int i = 0; i < n; i++){
            int index = search(matrix[i], target);
            if(index >= 0){
                return true;
            }
        }
        return false;
    }

    public int search(int[] arr, int target) {
        int left = 0, rigth = arr.length - 1;
        while(left <= rigth){
            int mid = (rigth - left) / 2 + left;//这种写法的优点是当left和right比较大时，可能不会超出范围
            if(arr[mid] == target){
                return mid;
            } else if(arr[mid] > target) {
                rigth = mid - 1;
            } else if(arr[mid] < target) {
                left = mid + 1;
            }
        }
        return -1;
    }
}
Dzhuser
关注
剑指offer刷题笔记.zip
05-13
这个压缩包“剑指offer刷题笔记.zip”显然包含了作者对这些面试题的解题思路、算法分析以及相关知识点的详细笔记。以下是对这些知识点的详细阐述： 1. **数据结构与算法** - **数组**：在《剑指Offer》中，数组是...
Java《剑指Offer》刷题笔记.zip
12-24
这份压缩包“Java《剑指Offer》刷题笔记.zip”显然包含了作者在阅读并实践这本书籍中的题目时所做的笔记。文件“note-coding-main”可能是笔记的主要内容目录或代码实现的存储位置。 以下是对Java《剑指Offer》中...
数对的最大曼哈顿距离[ABC178E] Dist Max
2301_80882026的博客
10-30 497
/曼哈顿距离化简绝对值之后最终可以化简为两种取最大的即可PII p[N];cin >> n;i <= n;
代码随想录训练营Day12 | 110.平衡二叉树 - 257二叉树的所有路径 - 404.左叶子之和 - 222.完全二叉树的节点个数
Zuoriqiufeng的博客
10-30 400
【代码】代码随想录训练营Day12 | 110.平衡二叉树 - 257二叉树的所有路径 - 404.左叶子之和 - 222.完全二叉树的节点个数。
xtu oj 连接字符串
Go offline for a while
10-30 963
最后总结一下：这题思路比较直观，找公共的元素，代码细节比较多，一个是要求输出字典序小的，第二是前面字符串要枚举完最后一个元素才算满足条件，第三是两个字符串可能完全没有公共部分，需要特判。
二分查找算法—C++
最新发布
2401_82677021的博客
11-03 317
关于求中点位置的操作什么时候需要加1，什么时候不需要。只需看下面的left和right ，如果出现-1，mid就需要加1。否则，不需要加1.
【力扣打卡系列】二分查找(搜索旋转排序数组)
qq_45734745的博客
10-29 304
坚持按题型打卡&刷&梳理力扣算法题系列，语言为go，Day11。
《Java 实现希尔排序：原理剖析与代码详解》
qq_69304031的博客
11-03 505
在排序算法的大家族中，希尔排序是一种改进的插入排序算法，它通过将原始数据分成多个子序列进行预排序，然后逐渐缩小子序列的间隔，最终对整个序列进行常规的插入排序，从而在一定程度上提高了排序的效率。希尔排序的基本思想基于插入排序，但它引入了一个间隔序列（也称为增量序列）的概念，使得排序过程不再是逐个元素地进行比较和插入，而是先对相隔一定间隔的元素进行比较和插入操作，随着排序的进行，间隔逐渐缩小，直到最后间隔为 1，此时就相当于进行了一次普通的插入排序。，经过希尔排序后，控制台会输出排序后的数组，其结果应该是。
JAVA学习-练习试用Java实现“数组排序”
weixin_69763181的博客
11-03 91
这个程序首先导入了'java.util.Arrays'和'java.util.Scanner'，然后定义了一个'main'方法。程序使用'Scanner'类来读取用户的输入，并将其分割成一个字符串数组。然后，它将字符串数组转换成整数数组，并使用'Arrays.sort'方法对整数数组进行排序。以下是一个Java程序，它使用内置的'Arrays.sort'方法对用户输入的整数数组进行排序。编写一个Java程序，对用户输入的整数数组进行排序（可以使用内置的Arrays.sort方法，也可以自己实现排序算法）。
迷宫求解：探索最优路径的算法与应用
liaozp88的博客
11-02 149
迷宫求解问题通常可以通过图搜索算法来解决，常用的方法包括广度优先搜索（BFS）、深度优先搜索（DFS）和A*算法。
数据结构+算法
HBryce24的博客
10-31 854
【代码】数据结构+算法。
【力扣打卡系列】二分查找（搜索旋转排序数组2）
qq_45734745的博客
10-29 269
坚持按题型打卡&刷&梳理力扣算法题系列，语言为go，Day10。
【力扣专题栏】字母异词分组，如何利用强大的容器（unordered_map）解决该问题？
2301_78704584的博客
11-03 107
【代码】【力扣专题栏】字母异词分组，如何利用强大的容器（unordered_map）解决该问题？
旋转翼巡检无人机飞行算法及关键技术综述！
YUNZHUO666的博客
10-30 606
PID控制器通过比较目标值与被控对象当前的反馈量，得到误差，并将误差值分别经过比例、积分、微分三个环节计算得到输出分量，三个分量加起来得到PID的输出，施加到被控对象上，使反馈量向目标值靠拢。例如，在俯仰运动中，通过改变前后端电机的转速差，产生不平衡力矩使机身绕y轴旋转，实现飞行器的俯仰运动。它实时采集各传感器测量的飞行状态数据，接收地面测控站的控制命令及数据，经计算处理后输出控制指令给执行机构，实现对无人机中各种飞行模态的控制和对任务设备的管理与控制。电机的转速和螺旋桨的尺寸需经过精确计算和优化。
连续数组和
TangKenny的博客
10-30 470
给定一个含有N个正整数的数组,求出有多少个连续区间(包括单个正整数),它们的和大于等于x。第一行两个整数Nx0N
数据结构与算法——Java实现 53.力扣938题——二叉搜索树的范围和
m0_73983707的博客
11-03 252
给定二叉搜索树的根结点root，返回值位于范围 [low, high]之间的所有结点的值的和。
二维数组查找与字符串空格替换的剑指offer刷题解析
"剑指offer刷题笔记是一份专注于技术面试题目的学习资料，主要涵盖C++、Python和Java等多种编程语言，作者完成了大约40多道题目。其中部分题目包括： 1. 有序数组找数字：在一个二维数组中，数组的每一行按升序排列...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Dzhuser

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值