定义
Pearson相关系数
评估两个连续变量之间的线性关系。
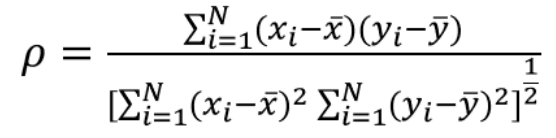
Spearman相关系数
评估两个变量之间的单调关系,在单调关系中,变量趋于一起变化,但不一定以恒定速率变化,即并非一定是线性关系。

区别
- 当有离群点时,Spearman会更加稳定。
创建一个数据集,并加上离群点,比较两种方法计算的相关系数。
x1 <- rnorm(200)
y1 <- rnorm(200) + .6 * x1
# 加入离群点
x2 <- c(x1, 14)
y2 <- c(y1, 14)
# Plot
par(mfrow=c(1,2))
plot(x1, y1, main="No outlier", col = 4, pch = 7, cex = 0.8)
plot(x2, y2, main="With outlier", col = 6, pch = 7, cex = 0.8)
# Calculate correlations
round(cor(x1, y1, method="pearson"), 2)
round(cor(x1, y1, method="spearman"), 2)
round(cor(x2, y2, method="pearson"), 2)
round(cor(x2, y2, method="spearman"), 2)

相关系数的结果如下:

即在没有离群点的时候,两者都是0.44;但是当存在离群点之后,pearson系数变成了0.69,但是spearman仍是0.44。
- Pearson相关系数表示线性关系,而Spearman并不一定是线性关系。
当一个变量增加时,另一个变量增加一致量,形成一条递增的直线,在该情况下二者的值均为+1。

当一个变量增加时另一个变量也增加,但是增量不完全一致,则此时Pearson相关系数为正但小于1,而Spearman相关系数仍为+1。

选择
- 连续数据,正态分布,线性关系,用pearson相关系数是最恰当,当然用spearman相关系数也可以, 就是效率没有pearson相关系数高。
- 上述任一条件不满足,就用spearman相关系数,不能用pearson相关系数。
- 两个定序数据之间也用spearman相关系数,不能用pearson相关系数。
注:
(1)定序数据是指仅仅反映观测对象等级、顺序关系的数据,是由定序尺度计量形成的,表现为类别,可以进行排序,属于品质数据。
eg. 优良差用123表示,加减乘除没有意义。定序数据最重要的意义代表了一组数据中的某种逻辑顺序。
(2)斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广,只要数据满足单调关系(例如线性函数、指数函数、对数函数等)就能够使用。
参考:
- https://blog.csdn.net/a_pickles/article/details/107347058
- https://www.jianshu.com/p/add3017e1c4f
- https://blog.csdn.net/lambsnow/article/details/79972145
- https://blog.csdn.net/Android_xue/article/details/100136612























 8万+
8万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








