计算几何(四)——多边形和圆（updating）

多边形

多边形

定义：由在同一平面且不再同一直线上的多条线段首尾顺次连接且不相交所组成的图形叫多边形

简单多边形

定义：简单多边形是除相邻边外其它边不相交的多边形

凸多边形

定义：过多边形的任意一边做一条直线，如果其他各个顶点都在这条直线的同侧，则把这个多边形叫做凸多边形。或者说如果一个简单多边形的内角不超过180°，那么它是凸多边形

性质：

1.任意凸多边形外角和均为$360$°

2.任意凸多边形内角和为$(n-2)\ast 180$°

struct Polygon{
	vector<Point> ps;  //逆时针序存入顶点集
};

多边形常用函数

多边形面积

如图所示，任何一个多边形（没错，是任意多边形）的面积都可以分为多个三角形的面积和。我们之前知道任意两个向量的叉乘是两条向量围成平行四边形的面积，那么除以二就是两个向量围成三角形的面积。所以我们可以从多边形点集中选择任意一点作为起点，向除它之外点连成向量，那么叉乘求和即可。这里面积实际上指的是有向面积。

除此之外，多边形面积还有一种计算方法，我们在多边形外任取一点$O$，按逆时针方向分别向多边形各点作向量。我们分别求出三角形$OAB$、$OBC$、$ODC$的有向面积（从向量 $OA$ 开始），那么这三个面积之和为为五边形$OABCD$的向上的正向有向面积，这时我们再求出三角形$ODA$的逆向面积（ $OD\times OA$ ），那么二者之和刚好是多边形$ABCD$的面积。实际上$O$点取在这个平面的任意一处均可求出多边形面积

//第一种思路
double polygonArea(vector<Point> &p){   //p为端点集合,点需要逆时针排序才保证得到正解
    double s=0.0;
    int n=p.size();
    for(int i=1;i<n-1;i++)
        s+=(p[i]-p[0])^(p[i+1]-p[0]);
    return s;
}

判断点在多边形内

非凸边形

1.射线法

对于要判断的点向右引一条射线，判断与直线的边的交点是否在该点右侧，统计数量，如果为奇数代表在多边形内，否则在多边形外

判断的原理是三角形相似，有：$(x-x_1):(x_2-x_1)=(y_0-y_1):(y_2-y_1)$

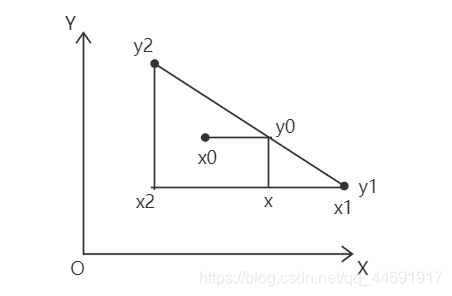
但是还要注意，当该点在线段的正下方或者正上方时都不需要判断，因为他们的交点在多边形外；当线段水平时不需要判断，因为无交点。

bool IsInPolygon(Point p,vector<Point> &py){
    int cnt=0,num=py.size();
    for (int i=0;i<py.size(); i++){
        Point p1=py[i],p2=py[(i+1)%num];
        if(p1.y==p2.y) continue;
        if(p.y<min(p1.y,p2.y)) continue;
        if (p.y>=max(p1.y,p2.y)) continue;
        double x=(p.y-p1.y)*(p2.x-p1.x)/(p2.y-p1.y)+p1.x;
        if (x>p.x) cnt++; //只统计单边交点
    }
    return cnt&1;
}

2.这种方法暂时没看懂，但是看起来和下面的凸多边形类似，都是先看点和起点连成的向量是否在边向量的左边，但是接着判断了$y$坐标的大小。

//判断点是否在多边形内，若点在多边形内返回1，在多边形外部返回0，在多边形上返回-1
int isPointInPolygon(Point p,vector<Point> py{
    int num=0;
    int n=py.size();
    for(int i=0;i<n;i++){
        if( isOnSeg(p,Line(py[i],py[(i+1)%n])) ) return -1;
        int k=dcmp((py[(i+1)%n]-py[i])^(p-py[i]));
        int d1=dcmp(py[i].y-p.y);
        int d2=dcmp(py[(i+1)%n].y-p.y);
        if(k>0 && d1<=0 && d2>0) num++;
        if(k<0 && d2<=0 && d1>0) num--;
    }
    if(num) return 1;
    return 0;
}

凸边形

如下图，我们任选一起点依次将多边形的边连成下面几个向量，那么如果点在凸多边形内部，有 $op$ 在 $oa$ 的左边（逆时针方向），前面学习点和向量时有一个函数ToLeftTest专门判断。而且不难发现如果$p$在凸多边形外，至少会出现一次不在多边形边向量左边的情况

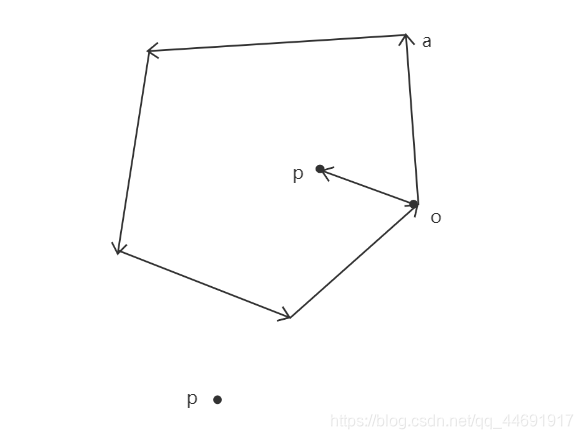
bool isPointInConvexPolygon(Point p,vector<Point> py){
    int n=py.size();
    for(int i=0;i<n;i++)
        if(!ToLeftTest(p,py[i],py[(i+1)%n])) return false;
    return true;
}

Pick定理

皮克定理是指一个计算点阵中顶点在格点上的简单多边形面积公式，该公式可以表示为

$2S=2a+b-2$

其中$a$表示多边形内部的点数，$b$表示多边形边界上的点数，$S$表示多边形的面积

如上图$a=39,b=14$，那么$S=(39\ast 2+14-2)/2=45$

注意到如果给定网格中的简单多边形，那么可以先求出面积再计算出边上有多少点，进而求出简单多边形内部有多少点

多边形简单模板

struct Polygon{
	vector<Point> ps;  
};

double polygonArea(vector<Point> &py){   //任意多边形面积
    double s=0.0;
    int n=py.size();
    for(int i=1;i<n-1;i++)
        s+=(py[i]-py[0])^(py[i+1]-py[0]);
    return s;
}


bool IsInPolygon(Point p,vector<Point> &py){  //点是否在多边形内部
    int cnt=0,num=py.size();
    for (int i=0;i<py.size(); i++){
        Point p1=py[i],p2=py[(i+1)%num];
        if(p1.y==p2.y) continue;
        if(p.y<min(p1.y,p2.y)) continue;
        if (p.y>=max(p1.y,p2.y)) continue;
        double x=(p.y-p1.y)*(p2.x-p1.x)/(p2.y-p1.y)+p1.x;
        if (x>p.x) cnt++;
    }
    return cnt&1;
}

圆

存储圆的半径和圆心坐标即可

struct Circle{
    Point o;
    double r;
    Circle(Point o,double r):o(o),r(r) {}
    Point point(double a){			//通过圆心角(弧度)求圆上一点坐标
        return Point(o.x+cos(a)*r,o.y+sin(a)*r);
    }
};

圆的常用函数

圆与直线的交点

直线$l$和圆$o$是已知的，那么我们先根据点到直线的距离公式求出距离，接着和$r$比较便可以知道该直线和圆是相离，相切还是相交。然后对于相交的情况，先求出圆心在直线上的投影点$s$，接着在三角形$ost$中，求出$|st|$的距离，接着根据向量$v$求出向量 $st$ ，最后由$s$点加减该向量即可得到该点。

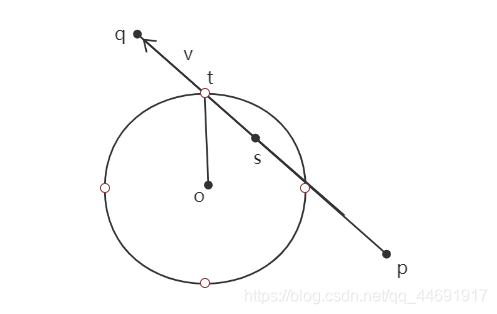
int getLineCircleInter(Line l,Circle c,vector<Point> &ans){
    double d=disToLine(c.o,l);
    if(dcmp(c.r-d)<0)   //相离
        return 0;
    else if(dcmp(c.r-d)==0){   //相切
        Point p=getPro(c.o,l);
        ans.push_back(p);
        return 1;
    }else{		//相交
  		Point p=getPro(c.o,l);
        double d1=sqrDis(c.o-p);
        double d2=sqrt(c.r*c.r-d1);
        Vector v=l.v*(d2/dis(l.v));
        Point p1=p+v;
        Point p2=p-v;
        ans.push_back(p1),ans.push_back(p2);
   		return 2; 
    }
}

圆和线段是否有交点

其实是比较好判断的，首先判断两端点是否有一点在圆上或圆内，如果有一点在圆内那么就在圆内。但是这里我把两端点均在圆内但没有交点的情况也算上了（具体题目具体分析）。接着判断圆心到线段的距离是否小于等于半径即可。

bool getLineCircleInter(Seg l,Circle c){
    if(sqrDis(l.p-c.o)<c.r*c.r || dcmp(sqrDis(l.p-c.o)-c.r*c.r)==0) return 1;
    if(sqrDis(l.q-c.o)<c.r*c.r || dcmp(sqrDis(l.q-c.o)-c.r*c.r)==0) return 1;
    if(disToSeg(c.o,l)<c.r || dcmp(disToSeg(c.o,l)-c.r)==0) return 1;
    return 0;
}

圆和简单多边形的相交面积