设有向图D = (V,E),顶点集V = {v1,v2,····,vn}。
定义矩阵
![]()
为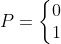 (当vi到vj不可达时,p为0;当vi到vj可达时p为1.)
(当vi到vj不可达时,p为0;当vi到vj可达时p为1.)
称矩阵P是图D的可达矩阵
一般地,设n阶有向图D的邻接矩阵为A,有A可得到图D的可达矩阵,不妨设为P,其步骤如下:
1、求出
2、把矩阵
设有向图D = (V,E),顶点集V = {v1,v2,····,vn}。
定义矩阵
![]()
为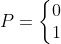 (当vi到vj不可达时,p为0;当vi到vj可达时p为1.)
(当vi到vj不可达时,p为0;当vi到vj可达时p为1.)
称矩阵P是图D的可达矩阵
一般地,设n阶有向图D的邻接矩阵为A,有A可得到图D的可达矩阵,不妨设为P,其步骤如下:
1、求出
2、把矩阵
 3798
3798

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


