算法设计:迭代、穷举搜索、递推、递归、回溯、贪心、动态规划、分治等算法设计。在算法设计中,主要考查动态规划法、分治法、回溯法、递归法、贪心法。
1.迭代法
迭代法是用于解决数值计算问题中的非线性方程(组)求解或最优解(近似根)的一种算法设计方法。它的主要思想是:从某个点出发,通过某种方式求出下一个点,使得其离要求的点(方程的解)更近一步;当两者之差接近到可接受的精度范围时,就认为找到了问题的解。由于它是不断进行这样的过程,因此称为迭代法,同时从中也可以看出使用迭代法必须保证其收敛性。
具体来说,迭代法包括简单迭代法、对分法、梯度法、牛顿法等。对分法是指在某个解空间采用二分搜索,它的优点是只要在该解空间内有根,就能够快速地搜索到;梯度法则又称为最速下降法,它常用于工程问题的解决。
在使用的迭代法的过程中,应该注意两种异常情况。
如果方程无解,那么近似根序列将不会收敛,迭代过程会成为“死循环”,因此在使用时应先判断其是否有解,并应对迭代的次数进行限制;
方程虽然有解,但迭代公式选择不当,或迭代的初始近似根选择不合理,也会导致迭代失败。
迭代法总的来说是一种比较简单的求解方法,但是此类算法还存在两个不足:一是一次只能求方程的一个解,而且需要人工给出近似初值,如果初值选择不好就可能找不到解;二是不易保证程序的收敛性。
2. 穷举搜索法
穷举搜索法是穷举所有可能的情形,并从中找出符合要求的解,即对可能是解的众多候选解按某种顺序逐一枚举和检验,并从中找出那些符合要求的解作为问题的解。对于没有有效的解法的离散型问题,如果规模不大,穷举搜索法是很好的选择。
穷举搜索法通常需要使用多重循环来实现,对每个变量的每个值都进行测试,看其是否满足给定条件,如果满足则说明找到问题的一个解。
3. 递推法
递推法实际上首先需要抽象为一种递推关系,然后再按递推关系来求解。它通常表示为两种方式:
从简单推到一般,这常用于计算级数;
将一个复杂问题逐步推到一个具有已知解的简单问题,它常与“回归”配合为递归法。
递推法是一种简单有效的方法,通常可以编写出执行效率较高的程序。使用的关键是找出递推关系式,并确定初值。
任何用递推法可以解决的问题,都可以很方便地用递归法解决;但有很多可以使用递归法解决的问题,不一定可以使用递推法解决。但如果是既可以使用递归,又可以使用递推法来解决的问题,则应使用递推法,因为它的效率要高于递归法。
4. 递归法
递归是一种特别有用的工具,不仅在数学中广泛应用,还是设计和描述算法的一种有力工具。它经常用于分解复杂算法:将规模为N的问题分解成为规模较小的问题,然后从这些规模较小的问题的解中构造出大问题的解;而这些规模较小的问题采用同样的分解和综合的方法,分解成规模更小的问题;而特别的,当规模为1时,能够得到解。
从上面的描述中,我们可以看出递归算法包括“递推”和“回归”两个部分:递推是为了得到问题的解,将它推到比原问题简单的问题的求解;而回归则是当小问题得到解后,回归到原问题的解上来。
在使用递推时应该注意以下几点:
递推应该有终止点,终止条件便会使算法失效;
“简单问题”表示离递推终止条件更为接近的问题。也就是说简单问题与原问题解的算法是一致的,差别主要是参数。参数的变化将使问题递推到有明确解的问题。
在使用回归时应该注意:
递归到原问题的解时,算法中所涉及的处理对象应是关于当前问题的,即递归算法所涉及的参数与局部处理对象是有层次的。当解一个问题时,有它的一套参数与局部处理对象。当递推进入一“简单问题”时,这套参数与局部对象便隐蔽起来,在解“简单问题”时,又有自己一套。但当回归时,原问题的一套参数与局部处理对象又活跃起来了。
有时回归到原问题以得到问题解,回归并不引起其他动作。
采用递归方法定义的数据结构或问题最适合使用递归方法解答。
当然,回到实际的开发中,递归的表现形式有两种:
函数自己调用自己。
两个函数之间相互调用。
考试时以函数自己调用自己的方式居多。下面以两个程序实例说明该问题。
例:利用递归程序计算n的阶乘。
这是一个非常简单的计算问题,只要学过程序设计,都能用一个简单的循环来解决该问题。编写一个循环语句,实现:S=1234…*n即可。但在此,我们要求用递归来实现,这便要求我们找出阶乘中隐藏的推荐规则,通过总结可得出规律:
也就是说:要求n的阶乘,需要分两种情况分析问题,当n=0时,阶乘的结果为1;当n不等于0时,n的阶乘等于n乘以(n-1)的阶乘。这样就产生了递推过程。下面是将这种思路进行程序实现:
接下来看一个更为复杂的例题:编写计算斐波那契(Fibonacci)数列的函数,数列大小为n。无穷数列1,1,2,3,5,8,13,21,35,…,称为斐波那契数列。这种数列有一个规律,数列第1个与第2个元素的值均为1,从第3个值开始,每个数据是前两个数据之和。即,数列可以表示为:
1,1,(1+1),(1+(1+1)),((1+1)+(1+(1+1)))…
在此,我们可以把这种规律转成递推式:
有了递推式,再来写程序,也就很容易了,直接转化即可,该问题程序实现如下所示:
使用递归法写出的程序非常简洁,但其执行过程却并不好理解。在理解这种方法的过程中,建议大家使用手动运行程序的方式来进行分析,先从最简单的程序开始尝试,逐步到复杂程序。递归法的用途非常广泛,图的深度优先搜索、二叉树的前序、中序和后序遍历等可采用递归实现。
5. 回溯法
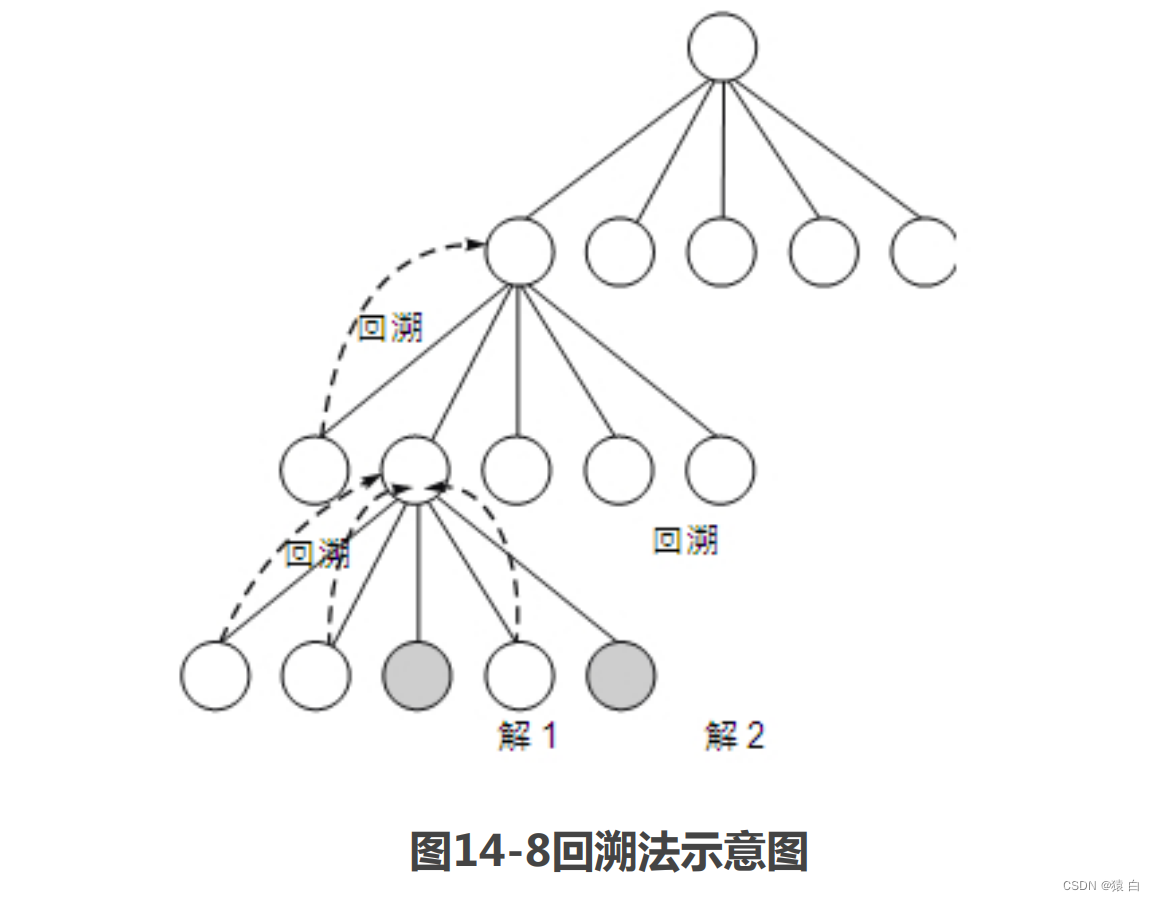
回溯法(试探法)是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。其工作机制如图14-8所示。
在使用回溯法时,必须知道以下几个关键的特性:
采用回溯法可以求得问题的一个解或全部解,为了不重复搜索已找过的解,通常会使用栈(也可以用位置指针、值的排列顺序等)来记录已经找到的解。
要注意的是,回溯法求问题的解时,找到的解不一定是最优解。
程序要注意记录中间每一个项的值,以便回溯;如果回溯到起始处,表示无解。
用回溯法求问题的全部解时,要注意在找到一组解时应及时输出并记录下来,然后马上改变当前项的值继续找下一组解,防止找到的解重复。
下面我们通过一个经典的问题来研究回溯法的应用。
例:使用回溯法解决迷宫问题,找到迷宫的出路。
基本思路分析:进入一个迷宫之所以难以找到出路,是因为迷宫会有多个岔路口,形成多条路径,而成千上万条路径中,仅有1条(或几条)路径可走出迷宫。若采用回溯法,则在尝试走一条路径时,会把这些分岔都记录好,当一条路走不通时,原路返回到最近的一个分岔口,从这个分岔口找下一路进行尝试,这个过程与14-8所示的情况完全一致。
接下来可以开始把这种思路转化为数据结构来表达了:
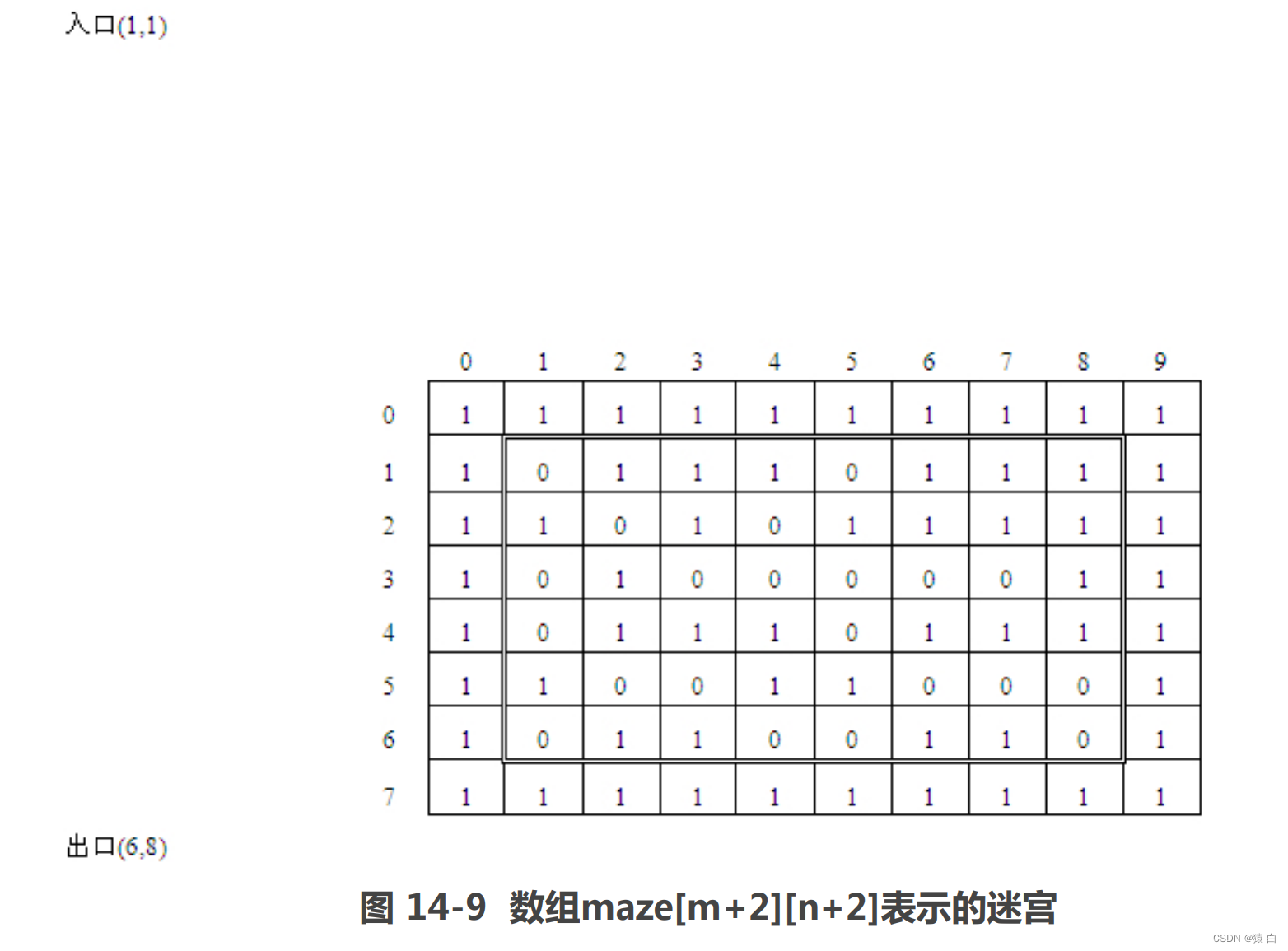
设迷宫为m行n列,利用数组maze[m][n]来表示一个迷宫。maze[i][j]=0或1。其中0表示通路,1表示不通。当从某点向下试探时,中间的点有8个方向可以试探,而4个角点只有3个方向,而其他边缘点有5个方向。为使问题简单化,我们用maze[m+2][n+2]来表示迷宫,而迷宫的四周的值全部为1。这样做使问题简单了,每个点的试探方向全部为8,不用再判断当前点的试探方向有几个,同时与迷宫周围是墙壁这一实际问题相一致。
如图14-9所示的迷宫是一个6×8的迷宫。入口坐标为(1,1),出口坐标为(6,8)。
迷宫的定义如下:
#define m 6 /* 迷宫的实际行 /
#define n 8 / 迷宫的实际列 */
int maze [m+2][n+2] ;
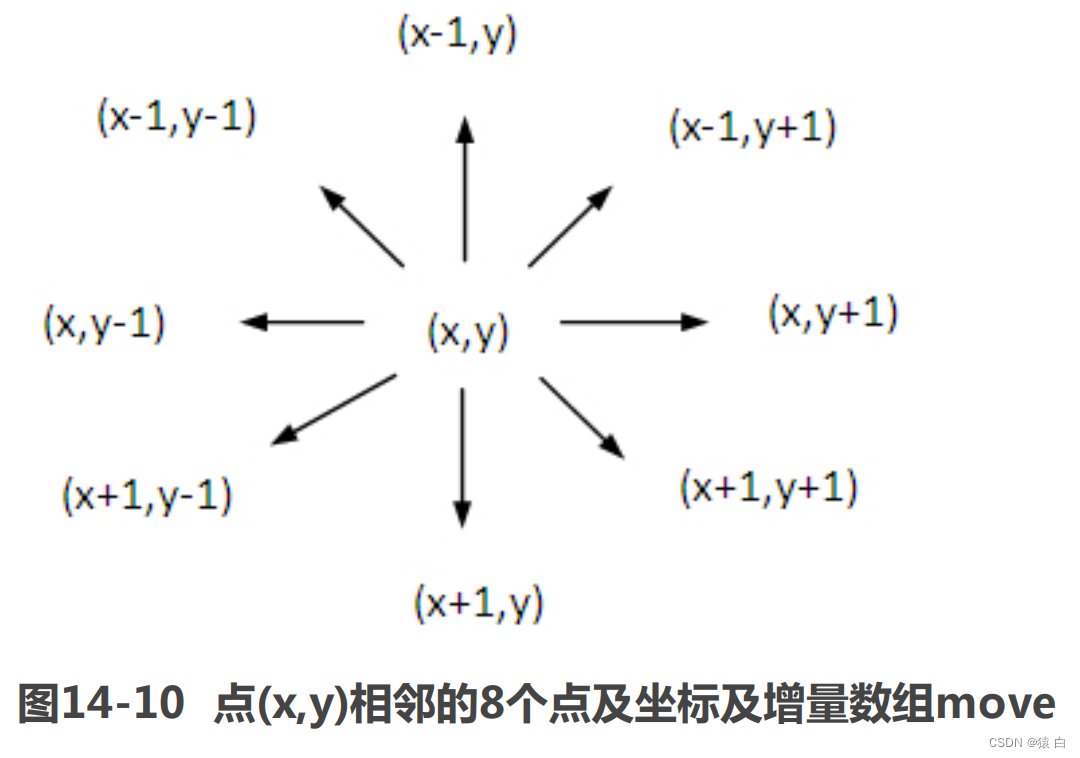
在上述表示迷宫的情况下,每个点有8个方向可以试探。如当前点的坐标为(x,y),与其相邻的8个点的坐标都可根据与该点的相邻方位而得到。因为出口在(m,n),因此试探顺序规定为:从当前位置向前试探的方向为从正东沿顺时针方向进行。为了简化问题,方便地求出新点的坐标,将从正东开始沿顺时针方向进行的这8个方向的坐标增量放在一个结构数组move[8]中,在move 数组中,每个元素由两个域组成,x为横坐标增量,y为纵坐标增量。move数组如图14-10所示。
move数组定义如下:
typedef struct
{
int x,y
} item ;
item move[8] ;
这样对move的设计会很方便地求出从某点(x,y)按某一方向v (0≤v≤7) 到达的新点(i,j)的坐标。
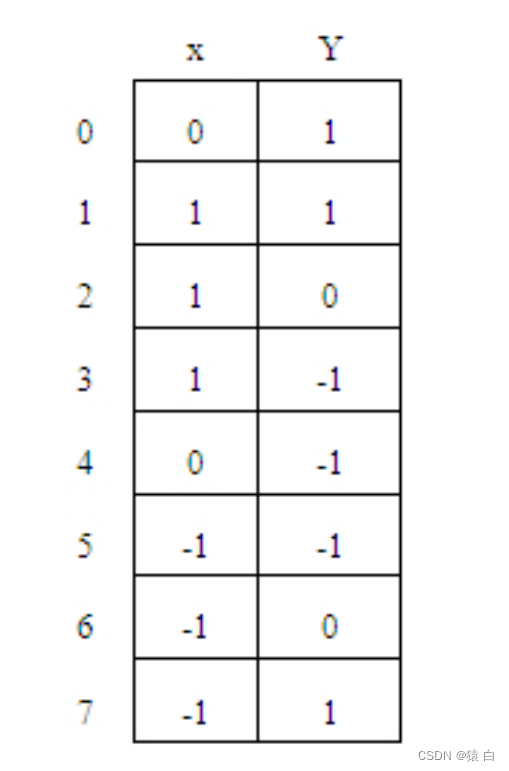
可知,试探点的坐标(i,j)可表示为i=x+move[v].x ;j=y+move[v].y。
到达了某点而无路可走时需返回前一点,再从前一点开始向下一个方向继续试探。因此,压入栈中的不仅是顺序到达的各点的坐标,而且还要有从前一点到达本点的方向。对于迷宫,依次入栈如下:
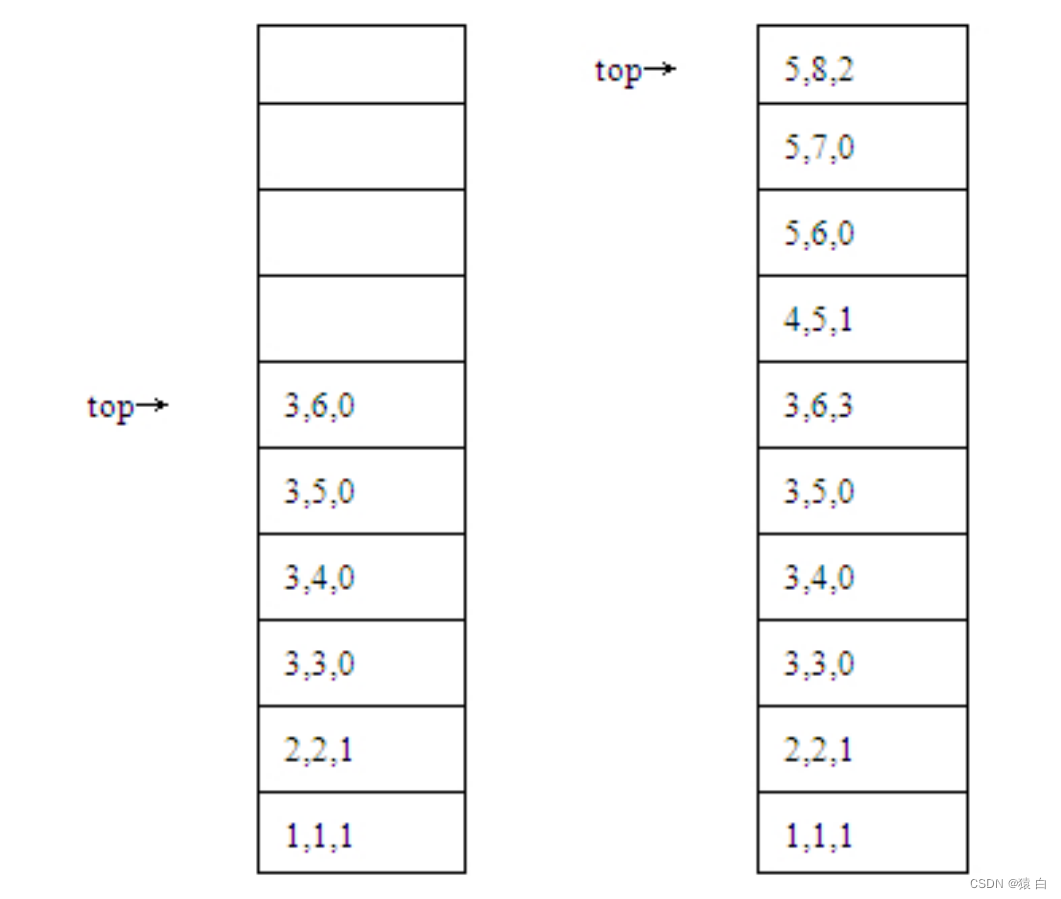
栈中每一组数据是所到达的每点的坐标及从该点沿哪个方向向下走的,对于如图14-9所示的迷宫,走的路线为:(1,1)1→(2,2)1→(3,3)0→(3,4)0→(3,5)0→(3,6)0(下脚标表示方向);当从点(3,6)沿方向0到达点(3,7)之后,无路可走,则应回溯,即退回到点(3,6),对应的操作是出栈,沿下一个方向即方向1继续试探;方向1、2试探失败,在方向3上试探成功,因此将(3,6,3)压入栈中,即到达了(4,5)点。栈中元素是一个由行、列、方向组成的三元组,栈元素的设计如下:
typedef struct
{int x , y , d ; /* 横坐标和纵坐标及方向*/
}datatype ;
栈的设计如下:
#define MAXSIZE 1024 /*栈的最大深度*/
typedef struct
{datatype data[MAXSIZE];
int top;/*栈顶指针*/
}SeqStack
一种方法是另外设置一个标志数组mark[m][n],它的所有元素都初始化为0,一旦到达了某一点(i,j)之后,使mark[i][j]置1,下次再试探这个位置时就不能再走了。另一种方法是当到达某点(i,j)后使maze[i][j]置-1,以便区别未到达过的点,同样也能起到防止走重复点的目的。本书采用后者方法,算法结束前可恢复原迷宫。
算法简单描述如下:
栈初始化;
将入口点坐标及到达该点的方向(设为-1)入栈
while (栈不空) {
栈顶元素=>(x , y , d)
出栈;
求出下一个要试探的方向d++;
while(还有剩余试探方向时){
if (d方向可走)
then { (x , y , d)入栈 ;
求新点坐标(i, j);
将新点(i , j)切换为当前点(x , y);
if ( (x ,y)= =(m,n) )结束 ;
else 重置d=0 ;
}
else d++ ;
}
}
该问题算法程序实现如下所示。
#include <stdio.h>
#define m 6 /* 迷宫的实际行 */
#define n 8 /* 迷宫的实际列 */
#define MAXSIZE 1024 /* 栈的最大深度 */
int maze[m+2][n+2]; /* 迷宫数组,初始时为0*/
typedef struct item{ /* 坐标增量数组 */
int x,y;
}item;
item move[8]; /* 方向数组 */
typedef struct datatype{ /* 栈结点数据结构 */
int x,y,d; /* 横坐标和纵坐标及方向 */
}datatype;
typedef struct SeqStack{ /* 栈结构 */
datatype data[MAXSIZE];
int top; /* 栈顶指针 */
}SeqStack;
SeqStack *s;
datatype temp;
int path(int maze[m+2][n+2],item move[8]){
int x,y,d,i,j;
temp.x=1;temp.y=1;temp.d=-1;
Push_SeqStack(s,temp); /* 辅助变量temp表示当前位置,将其入栈 */
while(!Empty_SeqStack(s))
{ Pop_SeqStack(s,&temp); /* 若栈非空,取栈顶元素送temp */
x=temp.x;y=temp.y;d=temp.d+1;
while(d<8) /* 判断当前位置的8个方向是否为通路 */
{ i=x+move[d].x;j=y+move[d].y;
if(maze[i][j]= =0)
{ temp.x=x;temp.y=y;temp.d=d;
Push_SeqStack(s,temp);
x=i;y=j;maze[x][y]=-1;
if(x==m&&y==n)return 1; /* 迷宫有路 */
else d=0;
}
else d++;
} /*while (d<8)*/
} /*while */
return 0 ; /* 迷宫无路 */
}
int Empty_SeqStack(SeqStack *s) /* 判断栈空函数 */
{ if (s->top= =-1)return 1;
else return 0;
}
int Push_SeqStack(SeqStack *s, datatype x) /* 入栈函数 */
{ if(s->top= =MAXSIZE-1)return 0; /* 栈满不能入栈 */
else {s->top++;
s->data[s->top]=x;
return 1;
}
}
int Pop_SeqStack(SeqStack *s,datatype *x) /* 出栈函数 */
{ if(Empty_SeqStack(s))return 0; /* 栈空不能出栈 */
else{*x=s->data[s->top];
s->top--;return 1; } /* 栈顶元素存入*x,返回 */
}
void main(){
int i,j,t;
move[0].x=0;move[0].y=1;
move[1].x=1;move[1].y=1;
move[2].x=1;move[2].y=0;
move[3].x=1;move[3].y=-1;
move[4].x=0;move[4].y=-1;
move[5].x=-1;move[5].y=-1;
move[6].x=-1;move[6].y=0;
move[7].x=-1;move[7].y=1;
for(i=0;i<=n+1;i++){
maze[0][i]=1;
maze[m+1][i]=1;
}
for(i=1;i<=m;i++){
maze[i][0]=1;
maze[i][n+1]=1;
}
printf("please input maze\n");
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)scanf("%d",&maze[i][j]);
t=path(maze,move);
if(t==1){
printf("the track is :\n");
while(!Empty_SeqStack(s))
{ Pop_SeqStack(s,&temp); /*若栈非空,则打印输出 */
printf("%d,%d,%d\n",temp.x,temp.y,temp.d);
}
}
}
6. 贪婪法
贪婪法,也叫贪心法,它是一种重要的算法设计技术,它总是做出当前来说最好的选择,而并不从整体上加以考虑,它所做的每步选择只是当前步骤的局部最优,而不一定是整体最优。由于它并不必为了寻找最优解而穷尽所有可能解,因此其耗费时间少,一般可以快速得到满意解(即“不追求最优,但求满意”)。
贪婪法只能够求问题的某个解,而不可能给出所有的解。经典的贪婪法算法包括背包问题、装箱问题、马踏棋盘问题、货郎担问题、哈夫曼编码问题。
如此解释很抽象,应用到一个实例中来说明问题。如一个超市的收银系统,要计算出最佳的找零方案,可以采用贪心法。假设找零金额为38元,贪心法的基本思路是:由于人民币面值为:100,50,20,10,5,1。为了找零时,找出的零钞张数最少,所以优先考虑面额大的,先用1张20块的,然后还需要找零18,此时再用1张10块的,再用1张5块的,接下来用3张一块的,这样就完成任务了。我们可以发现这个过程是按既定的顺序一步一步走,形成解决方案,这个过程中不涉及回溯。通过这个实例,可以了解到贪心法的基本思想。
下面将通过装箱问题来分析贪婪法的具体应用。
例:有6种物品,它们的体积分别为:60、45、35、20、20和20单位体积,箱子的容积为100个单位体积。现在求需要几只箱子才能把这些物品都装起来。
使用贪婪法求解该问题的基本思想是:先将物品的体积按从大到小的顺序排列。然后依次将物品放到它第一个能放进去的箱子中,若当前箱子装不下当前物品,则启用一个新的箱子装该物品,直到所有的物品都装入了箱子。如采用这种方式,我们发现,得到解决方案为:1、3号物品放一个箱子,2、4、5放第二个箱子,6放在第3个箱子,一共需要3个箱子。但由于此问题很简单,我们可以很容易用人工计算的方式得知最优解只要2个箱子。即:1、4、5和2、3、6。所以从此可以看出贪婪法求的是可行解,而非最优解。下面是该问题的算法与程序实现过程。
算法简单描述:
{输入箱子的容积;
输入物品种数n;
按体积从大到小顺序,输入各物品的体积;
预置已用箱子链为空;
预置已用箱子计数器box_count为0;
for (i=0;i<n;i++)
{从已用的第一只箱子开始顺序寻找能放入物品i 的箱子j;
if (已用箱子都不能再放物品i)
{新启用一个箱子,并将物品i放入该箱子;
box_count++;
}
else
将物品i放入箱子j;
}
}
上述算法一次就能求出需要的箱子数box_count,并能求出各箱子所装物品,但该算法不一定
能找到最优解。
该问题算法程序实现如下所示。
# include<stdio.h>
# include<stdlib.h>
typedef struct ele{/*物品结构的信息*/
int vno; /*物品号*/
struct ele *link; /*指向下一物品的指针*/
}ELE;
typedef struct hnode{/*箱子结构信息*/
int remainder; /*箱子的剩余空间*/
ELE *head; /*箱子内物品链的首元指针*/
struct hnode *next; /*箱子链的后继箱子指针*/
}HNODE;
void main()
{int n, i, box_count, box_volume, *a;
HNODE *box_h, *box_t, *j;
ELE *p, *q;
printf("输入箱子容积\n"); scanf("%d",&box_volume);
printf("输入物品种数\n"); scanf("%d",&n);
a=(int *)malloc(sizeof(int)*n);
printf("请按体积从大到小顺序输入各物品的体积:");
for (i=0;i<n;i++)scanf("%d",a+i); /*数组a按从大到小顺序存放各物品的体积信息*/
box_h=box_t=NULL; /*box_h为箱子链的首元指针,box_t为当前箱子的指针,初始为
空*/
box_count=0; /*箱子计数器初始也为0*/
for (i=0;i<n;i++) /*物品i按下面各步开始装箱*/
{p=(ELE *)malloc(sizeof(ELE));
p->vno=i; /*指针p指向当前待装物品*/
/*从第一只箱子开始顺序寻找能放入物品i的箱子j*/
for (j=box_h;j!=NULL;j=j->next)
if (j->remainder>=a[i])break; /*找到可以装物品i的箱子,贪婪准则的体现*/
if (j= =NULL) { /*已使用的箱子都不能装下当前物品i*/
j=(HNODE *)malloc(sizeof(HNODE)); /*启用新箱子*/
j->remainder=box_volume-a[i]; /*将物品i放入新箱子j*/
j->head=NULL; /*新箱子内物品链首元指针初始为空*/
if (box_h= =NULL) box_h=box_t=j; /*新箱子为第一个箱子*/
elsebox_t=boix_t->next=j; /*新箱子不是第一个箱子*/
j->next=NULL;
box_count++;
}
elsej->remainder-=a[i]; /*将物品i放入已用过的箱子j*/
/*物品放入箱子后要修改物品指针链*/
for (q=j->head;q!=NULL&&q->link!=NULL;q=q->link);
if (q= =NULL) { /*新启用的箱子插入物品*/
p->link=j->head; j->head=p; /*p为指向当前物品的指针*/
}
else{/*已使用过的箱子插入物品*/
p->link=NULL; q->link=p; /*q为指向箱子内物品链顶端的物品*/
}
}
printf("共使用了%d只箱子", box_count);
printf("各箱子装物品情况如下:");
for (j=box_h,i=1;j!=NULL;j=j->next,i++) /*输出i只箱子的情况*/
{printf("第%2d只箱子,还剩余容积%4d,所装物品有;\n",i,j->remainder);
for (p=j->head;p!=NULL;p=p->link)
printf("%4d",p->vno+1);
printf("\n");
}
}
7. 分治法
分治法可能算得上是使用最广泛的一种算法设计方法,其基本思想是将大问题分解成一些较小的问题,然后由小问题的解方便地构造出大问题的解。
采用分治法时,应该知道如果不能找到有效的将大问题分析为小问题的方法,那就可能无法得到问题的解;另外它也经常和递归法结合使用;在分治时要注意确保边界的清晰。分治法能够解决的问题通常具有以下特性:
问题缩小到一定程度将很容易解决——通常都能够满足。
问题可以分解为若干规模小的相同问题,这也称为最优子结构性质——前提条件。
利用该问题分解出的子问题的解可以合并为该问题的解——关键,如果只满足前两个,可以考虑使用贪婪法或动态规划法。
该问题所分解出的各个子问题是相互独立——和效率相关。
分治法最简单好理解的实例就是使用二分查找法进行查找。其程序实现如下所示。
function Binary_Search(L,a,b,x);
{ if(a>b)return(-1);
else
{ m=(a+b)/2;
if(x= =L[m])return(m);
else if(x>L[m])
return(Binary_Search(L,m+1,b,x)); /*递归实现*/
else return(Binary_Search(L,a,m-1,x)); /*递归实现*/
}
}
在以上算法中,L为排好序的线性表,x为需要查找的元素,b、a分别为x的位置的上下界,即如果x在L中,则x在L[a…b]中。每次我们用L中间的元素L[m]与x比较,从而确定x的位置范围,然后递归地缩小x的范围,直到找到x。
8. 动态规划法
动态规划法的基本思想与分治法类似,也是将复杂的问题分解成子问题来解决。但只是此处的子问题通常是重叠的,它们是将复杂问题的某些阶段,所以处理方式也有所不同。在此方法中,引入一个数组,不管子问题是否对最终解有用,都会存于该数组中,利用对数组的分析得到最优解。
在求解问题中,对于每一步决策,列出各种可能的局部解,再依据某种判定条件,舍弃那些肯定不能得到最优解的局部解,在每一步都经过筛选,以每一步都是最优解来保证全局是最优解,这可以划分成若干个阶段,问题的求解过程就是对若干个阶段的一系列决策过程。
每个阶段有若干个可能状态。
一个决策将你从一个阶段的一种状态带到下一个阶段的某种状态。
在任一个阶段,最佳的决策序列和该阶段以前的决策无关。
各阶段状态之间的转换有明确定义的费用,而且在选择最佳决策时有递推关系(即动态转移方程)。
使用动态规划法求解问题的基本思路如图14-11所示。
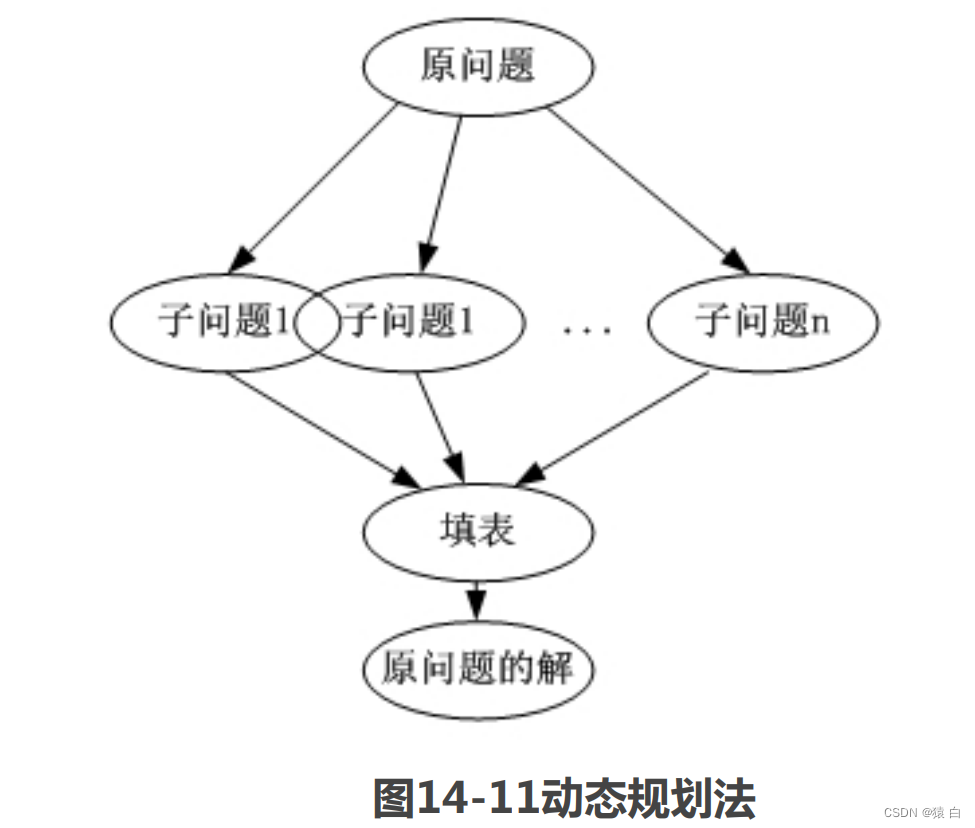
下面我们用一个通俗的例子,更进一步理解动态规划法:
假如我们要生产一批雪糕,在这个过程中要分好多环节:购买牛奶,对牛奶提纯处理,放入工厂加工,对加工后的商品进行包装,包装后就去销售……,这样每个环节就可以看做是一个阶段;产品在不同的时候有不同的状态,刚开始时只是白白的牛奶,进入生产后做成了各种造型,从冷冻库拿出来后就变成雪糕。每个形态就是一个状态,那从液态变成固态经过了冰冻这一操作,这个操作就是一个决策。一个状态经过一个决策变成了另外一个状态,这个过程就是状态转移。也就是说,在利用动态规划法解决问题时,我们会关注这些状态,以及状态的转移,对于中间结果,会予以保存,这样才能进行下一步的处理。
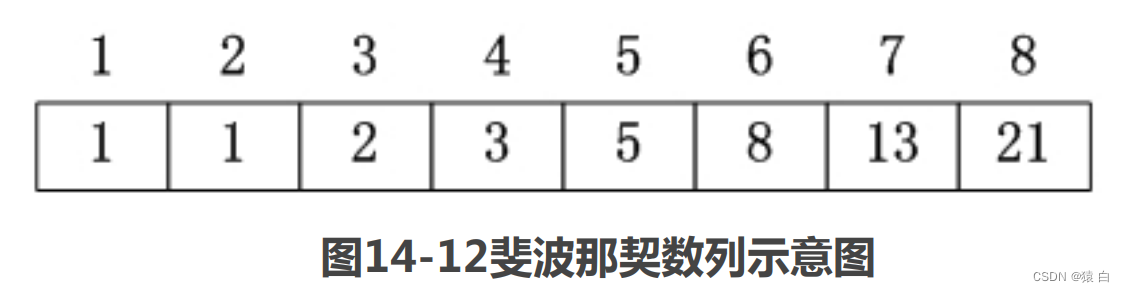
回到计算机方面的问题,同样是计算斐波那契(Fibonacci)数列,动态规划法的处理方式与递归法有一些差异,动态规划法一般要求填充一个表,如图14-12所示。
这个表存储的内容,其实就是中间结果,每一个中间结果存储下来,对于后续要求的内容起到了直接的影响。如,数列的第一个元素是1,这被要求填入表中的第1项,第2个元素也为1,也将存储起来。当要求F(3)时,通过查表,得到F(1)与F(2)的值,将两者相加得到F(3),再将F(3)的值存储到表格第3项中。依此类推,当要求计算出F(9)的值时,可通过查表得到F(7)、F(8)之后相加得到F(9)。这便是动态规划法解决问题的方法。通过上面的分析,相信大家对动态规划法的基本理念有一定的认知了,但现在要解决考试当中
的问题,往往还很难。因为考试往往涉及到程序实现的问题,下面将通过实例描述动态规划法的实现过程。
例:使用动态规划法解决背包问题。有一个背包总容量为42,现有三个物品的价值/重量分别为:40/3,101/31,67/10,请求出背包应该装哪些物品。
使用动态规划法解决这种0-1背包问题的基本思路为:将原问题分解成一系列子问题,然后从这些子问题中求出原问题的解。对一个负重能力为m的背包,如果选择装入第i种物品,那么原背包问题就转化为一个子背包问题了。动态规划会利用空间换时间,将子问题和其结果记录下来,这样一步一步查询得到最终结果。本题的实现代码为:
#include<iostream>
int c[10][100];/*对应每种情况的最大价值*/
int knapsack(int m,int n)
{
int i,j,w[10],p[10];
for(i=1;i<n+1;i++)
scanf("%d,%d",& w[i],& p[i]);
for(i=0;i<10;i++)
for(j=0;j<100;j++)
c[i][j]=0;/*初始化数组*/
for(i=1;i<n+1;i++)
for(j=1;j<m+1;j++)
{
if(w[i]<=j) /*如果当前物品的容量小于背包容量*/
{
if(p[i]+c[i-1][j-w[i]]>c[i-1][j])
/*如果本物品的价值加上背包剩下的空间能放的物品的价值*/
/*大于上一次选择的最佳方案则更新c[i][j]*/
c[i][j]=p[i]+c[i-1][j-w[i]];
else
c[i][j]=c[i-1][j];
}
else c[i][j]=c[i-1][j];
}
printf("背包中放着重量如下的物品:"); /*确定选取了哪几个物品*/
i=n;j=m;
while((i>=0)&&(j>=0))
{
if((p[i]+c[i-1][j-w[i]]>c[i-1][j])&&(i-1>=0)&&(j-w[i]>=0)){
printf("%d ",w[i]);
j=j-w[i];
i=i-1;
}
else
i=i-1;
}
printf("\n");
return(c[n][m]);
}
void main()
{
int m,n,k;
printf("输入总背包容量:");scanf("%d",&m);
printf("\n");
printf("输入背包最多可放的物品个数:");scanf("%d",&n);
printf("\n");
printf("输入每一组数据:");
printf("\n");
k=knapsack(m,n);
printf("背包所能容纳的最大价值为:%d。",&k);
}
练习
试题1
某货车运输公司有一个中央仓库和n个运输目的地,每天要从中央仓库将货物运输到所有运输目的地,到达每个运输目的地一次且仅一次,最后回到中央仓库。在两个地点i和j之间运输货物存在费用Cij。为求解旅行费用总和最小的运输路径,设计如下算法:首先选择离中央仓库最近的运输目的地1,然后选择离运输目的地1最近的运输目的地2,…,每次在需访问的运输目的地中选择离当前运输目的地最近的运输目的地,最后回到中央仓库。刚该算法采用了__(1)算法设计策略,其时间复杂度为(2)__。
(1)A.分治 B.动态规划 C.贪心 D.回溯
试题2
迪杰斯特拉(Dijkstra)算法用于求解图上的单源点最短路径。该算法按路径长度递增次序产生最短路径,本质上说,该算法是一种基于__(3)__策略的算法。
(3)A.分治 B.动态规划 C.贪心 D.回溯
试题3
在有n个无序无重复元素值的数组中查找第i小的数的算法描述如下:任意取一个元素r,用划分操作确定其在数组中的位置,假设元素r为第k小的数。若i等于k,则返回该元素值;若i小于k,则在划分的前半部分递归进行划分操作找第i小的数;否则在划分的后半部分递归进行划分操作找第k-i小的数。该算法是一种基于__(4)__策略的算法。
(4)A.分治 B.动态规划 C.贪心 D.回溯
试题4
要在8*8的棋盘上摆放8个“皇后”,要求“皇后”之间不能发生冲突,即任何两个“皇后”不能在同一行、同一列和相同的对角线上,则一般采用__(5)__来实现。
(5)A.分治法 B.动态规划法 C.贪心法 D.回溯法
试题5
分治算法设计技术__(6)__。
(6)A.一般由三个步骤组成:问题划分、递归求解、合并解
B.一定是用递归技术来实现
C.将问题划分为k个规模相等的子问题
D.划分代价很小而合并代价很大
试题6
用动态规划策略求解矩阵连乘问题M1M2M3M4,其中M1(205)、M2(535)、M3(354)和M4(4*25),则最优的计算次序为__(7)__。
(7)A.((M1*M2)*M3)*M4 B.(M1*M2)*(M3*M4)C.(M1*(M2*M3))*M4 D.M1*(M2*(M3*M4))
试题7
__(8)__不能保证求得0-1背包问题的最优解。
(8)A.分支限界法 B.贪心算法 C.回溯法 D.动态规划策略
答案
试题1分析
根据题目描述“每次在需访问的运输目的地中选择离当前运输目的地最近的运输目的地”我们
不难知道,每次都是选择当前看来最好的情况,因此这是一种贪心算法的设计策略。由于有n个目的
地要选择,每选择一个目的地时,需要在所以的目的地中选择出一个最优情况,所以总的时间复杂
度为 。
试题1答案
(1)C(2)A
试题2分析
分治法:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解
决;否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这
些子问题,然后将各子问题的解合并得到原问题的解。
动态规划法:这种算法也用到了分治思想,它的做法是将问题实例分解为更小的、相似的子问
题,并存储子问题的解而避免计算重复的子问题。
贪心算法:它是一种不追求最优解,只希望得到较为满意解的方法。贪心算法一般可以快速得
到满意的解,因为它省去了为找到最优解而穷尽所有可能所必须耗费的大量时间。贪心算法常以当
前情况为基础做最优选择,而不考虑各种可能的整体情况,所以贪心算法不要回溯。
回溯算法(试探法):它是一种系统地搜索问题的解的方法。回溯算法的基本思想是:从一条
路往前走,能进则进,不能进则退回来,换一条路再试。其实现一般要用到递归和堆栈。
针对单源最短路径问题,由Dijkstra提出了一种按路径长度递增的次序产生各顶点最短路径的算
法。若按长度递增的次序生成从源点s到其他顶点的最短路径,则当前正在生成的最短路径上除终点
以外,其余顶点的最短路径均已生成(将源点的最短路径看做是已生成的源点到其自身的长度为0的
路径)。这是一种典型的贪心策略,就是每递增一次,经对所有可能的源点、目标点的路径都要计
算,得出最优。
带权图的最短路径问题即求两个顶点间长度最短的路径。其中:路径长度不是指路径上边数的
总和,而是指路径上各边的权值总和。
试题2答案
(3)C
试题3分析
在解答本题前请参看本节考点精讲中的常用算法描述,当了解完选项中的各种算法特点后,可
以发现本题采用了分治法的策略思想。
试题3答案
(4)A
试题4分析
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原
先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法。回溯
法求解的过程其实是搜索整个解空间,来找到最优的解。而“皇后”问题是一个典型的用回溯法求
解的问题。
试题4答案
(5)D
试题5分析
分治的基本思想就是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较
小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相
同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。
所以分治算法设计技术主要包括三个步骤,分别是问题划分、递归求解、合并解。
试题5答案
(6)A
试题6分析
这个题目的关键是要求最优的计算次序,也就是要求计算过程中,乘法的次数最小。如果用选
项A的次序来计算,需要计算的乘法次数为:20535+20354+20425。同样我们可以求出其它
三种方法所需的乘法次数。其中最小的是选项C的5354+2054+20425。
试题6答案
(7)C
试题7分析
分支限界法一般以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间,那么肯
定能找出最优解。
贪心算法的思想是:总是做出在当前来说是最好的选择,而并不从整体上加以考虑,它所做的
每步选择只是当前步骤的局部最优选择,但从整体来说不一定是最优的选择。所以用该算法并不能
保证求得0-1背包问题的最优解。
回溯法的思想是:按选优条件向前搜索,以达到目标。但当搜索到某一步时,发现原先选择并
不优或达不到目标,就退回一步重新选择。它其实是遍历了整个解空间,所以肯定能找到最优解。
动态规划法的思想是:在求解问题中,对于每一步决策,列出各种可能的局部解,再依据某种
判定条件,舍弃那些肯定不能得到最优解的局部解,在每一步都经过筛选,以每一步都是最优解来
保证全局是最优解。它能求得0-1背包问题的最优解。
试题7答案
(8)B








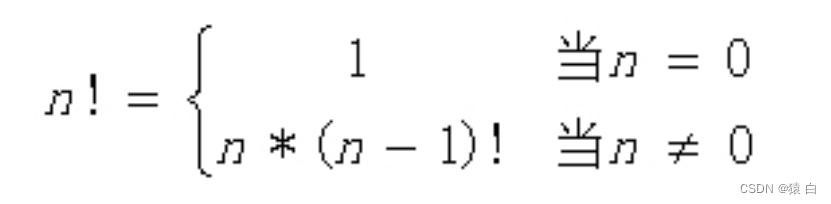

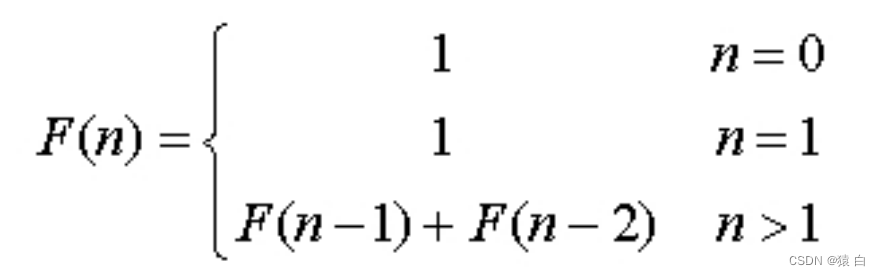

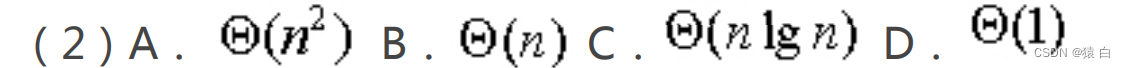














 3488
3488











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








