高维高斯过程建模与贝叶斯优化的应用调查
摘要
贝叶斯优化(BO),也就是应用贝叶斯函数近似法寻找代价函数的最优值,在近几年大受欢迎。特别是,在需要优化的参数较多的问题上提高其效率受到了极大的关注。这种关注已经渗透到高维BO的主力,即高维高斯过程回归,这也是独立的兴趣。高斯过程先验的巨大灵活性在为复杂的低维表面建模时是一个福音,但当维度增长过大时就显得太少了。从变量选择和加法分解到低维嵌入等等,各种结构模型的假设已经被测试过,以控制高维度。大多数这些方法反过来也需要修改获取函数优化策略。 在这里,我们回顾了定义的结构模型假设,并讨论了这些方法在实践中的好处和缺点。
1 引言
经常提到大量参数(高维)是黑盒优化的关键挑战。问题的根源在于所谓的维度诅咒,正如贝尔曼所创造的:复杂度与输入维数的指数依赖关系。在评估预算有限的情况下更是如此,在这种情况下,依赖代理(或元模型)是一种常见的做法。在贝叶斯优化(BO)中,变量的数量影响高斯过程(GP)代理(通过高维距离的行为),以及对下一个设计的搜索(因为它影响采集函数,在 BO 中用于搜索下一个要查询的设计)。大多数现有评论中都提到了维度缩放困难;因此,本文是渐进式的,重点关注几个方面(例如工程、运筹学和机器学习)的最新趋势,但绝不是详尽无遗的。
我们在这里关注 GP 代理,其受欢迎程度源于其建模灵活性和吸引人的不确定性量化 (UQ) 属性。可以考虑其他替代方案,但可能不会放弃一定程度的灵活性或小样本效率。例如,请参见树形模型的使用,如随机森林回归,树状结构的Parzen估计器,贝叶斯加性回归树,具有贝叶斯自适应样条的样条模型或者神经网络替代模型,如贝叶斯神经网络和用于优化的深度高斯过程。与 GP 密切相关的径向基函数(RBF) 插值在此设置中也很流行,但相对缺乏 UQ 功能。
在贝叶斯优化中,变量的数量会影响 GP 代理(通过高维距离的行为),以及使用采集函数搜索下一个设计(通过使其优化复杂化)。具体来说,保持相同近似质量所需的设计点数量随变量数量呈指数增长,并且体积集中在搜索空间的边界上。因此,设计相对分散在高维空间上。优化采集函数以选择下一个设计点受益于(相对)快速评估和梯度评估,但仍然受到这些相同的高维效应的影响。根据优化问题的难度,这些问题可能会在达到10个变量时发生,或者显示其中几十个变量。尽管如此,在相当有限的假设下,专门的方法已经被证明适用于数十亿个变量。
事实上,随着维度的增加,需要更强的结构模型假设,主要有三个类别。一种想法是通过删除对输出影响很小或没有影响的变量来减少维数,这将在第3.1节中进行讨论。另一种方法是假设变量或变量组的影响具有可加性,如第 3.2 节所述。在第3.3节中提出的最后一个方向是基于原始变量的线性或非线性组合来定义一些新的变量。图1显示了这些不同的结构建模选项,突出显示了选项之间的链接。随着学习结构的增加,模型推理变得更加困难,上述困难增加了估计风险。毫无疑问,可以通过避免估计来降低估计风险,这也是研究人员依赖随机定义的结构所采取的方法(尽管显然这是以随机化过程可能获得的方差和偏差为代价的)。然而,如果我们要推断结构,那么我们还必须面对这样一个事实,即在顺序设计框架中,最初只有有限的数据可用于估计函数的特征。要么可以在观察数据时“在线”学习和更新结构,要么我们可以将顺序过程分成两个连续的阶段,第一个阶段专注于估计结构,第二个阶段专注于利用它。在后一种情况下,用于每个阶段的最佳预算平衡可能相当依赖于问题。
所选择的结构以几个方式影响采集阶段。它可以用于建模工作,如在降维或可加性假设中,或者它可以约束优化域以帮助获取函数搜索。独立地,诸如在 Eriksson 中部署信任区域之类的策略也可用于通过限制搜索区域的体积来限制维度灾难的影响。由此产生的优化方法更具有局部性,但通过重新启动来补充全球化。
 图1 结构模型假设的分类法,从更简单的(顶部)到更一般的假设(底部)。箭头标志着可以推广的模型,(†)表示需要对噪声项进行估计,(‡)表示需要填充策略的情况,除非只在低维流形上进行优化。
图1 结构模型假设的分类法,从更简单的(顶部)到更一般的假设(底部)。箭头标志着可以推广的模型,(†)表示需要对噪声项进行估计,(‡)表示需要填充策略的情况,除非只在低维流形上进行优化。
GP 和 BO 存在许多额外的挑战和改进,这些挑战和改进超出了这里的范围,因此可能需要针对高维度调整相应的技术。其中一个问题是设计点数量的缩放。从逻辑上讲,需要更多的设计来学习更大的维度,但我们不能希望匹配对维度的指数依赖性。处理大数据的技术也引起了很多关注,其中一些是独立于输入维数的,就像局部模型一样。一般来说,我们在这里会假设,与运行BO框架相比,运行黑匣子仍然是有限制的。 可以对GP和BO进行其他改进,以应对复杂的噪声建模(如非高斯噪声、输入依赖方差)或非平稳性,但高维度会加剧学习任务的难度。虽然我们专注于无约束优化,但也可以考虑批量(或并行)优化、约束优化等。 我们将感兴趣的读者推荐给 Garnett [2022],以获得更广泛和更具介绍性的 BO 概述。
本文的其余部分内容如下。首先,在第2节中介绍了关键概念和符号。接下来,在第3节中详细介绍了高维GP建模的结构假设,然后在第4节中介绍了获取函数优化的后果和调整。第5节包括一个可能的测试函数列表。最后,第6节给出了一些实践指南和对有前景的研究方向的总结。
2 背景
让我们考虑一个代价评估的黑盒模拟器
f
:
X
⊂
R
d
→
R
f : X ⊂ R^d \rightarrow R
f:X⊂Rd→R,我们希望对其进行全局优化:
f
i
n
d
x
∗
∈
a
r
g
m
i
n
x
∈
X
f
(
x
)
(1)
find \ \pmb x^* \in argmin_{\pmb x \in X} f(\pmb x) \tag{1}
find xx∗∈argminxx∈Xf(xx)(1)
所谓黑箱,我们的意思是假定对f的函数形式一无所知:
f
(
x
)
f(x)
f(x)只能在任何给定的输入点x被查询(有时也假定梯度可用)。
2.1 高斯随机过程
给定一个索引集 X \mathcal X X ,在我们的例子中通常是 R d \mathbb R^d Rd 的封闭有界子集,随机过程只是一个规则,用于为 B B B 成员分配集合 x ( 1 ) , x ( 2 ) , . . . , x ( B ) x(1),x(2),...,x(B) x(1),x(2),...,x(B) 的随机变量的联合分布;相对于某些主要度量,也许它具有密度 δ ( y ( x ( 1 ) ) , y ( x ( 2 ) ) , . . . , y ( x ( B ) δ(y(x(1) ),y(x(2) ),...,y(x(B) δ(y(x(1)),y(x(2)),...,y(x(B) 。如果假设联合分布是高斯分布,那么我们只需要一种方法来确定任何可能的 B B B 点集合的平均向量和协方差矩阵将是什么。这些自然被称为先验均值函数 μ μ μ 和协方差函数 k k k (也是核函数)。这样的数学构造合在一起称为高斯过程 (GP) 。
如果我们观察到
y
(
x
∗
)
y(x^∗)
y(x∗) (可能被高斯噪声破坏),那么我们可以想象有一些随机过程将
x
(
1
)
,
x
(
2
)
,
.
.
.
,
x
(
B
)
x(1),x(2),...,x(B)
x(1),x(2),...,x(B) 映射到
δ
(
y
(
x
(
1
)
)
,
y
(
x
(
2
)
)
,
.
.
.
,
y
(
x
(
B
)
)
∣
y
(
x
∗
)
)
δ(y(x(1) ),y(x(2) ),...,y(x(B) )| y(x^∗))
δ(y(x(1)),y(x(2)),...,y(x(B))∣y(x∗)),也就是说,在给定
y
(
x
∗
)
y(x^∗)
y(x∗) 的情况下,将任何点集映射到其条件分布。令人高兴的是,这种新的随机过程也恰好是GP (相对于正态似然的共轭),并且其新的均值和协方差函数以封闭形式可用。特别是,如果我们观察到
y
(
x
(
1
)
)
,
.
.
.
,
y
(
x
(
n
)
)
y(x(1) ),...,y(x(n))
y(x(1)),...,y(x(n)) ,则
m
n
(
x
)
=
μ
+
k
(
x
)
⊤
K
−
1
(
y
−
μ
1
)
m_n(\mathbf{x})=\mu+\mathbf{k}(\mathbf{x})^{\top} \mathbf{K}^{-1}(\mathbf{y}-\mu 1)
mn(x)=μ+k(x)⊤K−1(y−μ1)
s
n
2
(
x
)
=
k
(
x
,
x
)
−
k
(
x
)
⊤
K
−
1
k
(
x
)
s_n^2(\mathbf{x})=k(\mathbf{x}, \mathbf{x})-\mathbf{k}(\mathbf{x})^{\top} \mathbf{K}^{-1} \mathbf{k}(\mathbf{x})
sn2(x)=k(x,x)−k(x)⊤K−1k(x)
其中
y
:
=
(
y
1
,
…
,
y
n
)
\mathbf{y}:=\left(y_1, \ldots, y_n\right)
y:=(y1,…,yn) ,
k
(
x
)
:
=
(
k
(
x
,
x
(
i
)
)
)
1
≤
i
≤
n
\mathbf{k}(\mathbf{x}):=\left(k\left(\mathbf{x}, \mathbf{x}^{(i)}\right)\right)_{1 \leq i \leq n}
k(x):=(k(x,x(i)))1≤i≤n,
K
:
=
(
k
(
x
(
i
)
,
x
(
j
)
+
τ
2
1
i
=
j
)
1
≤
i
,
j
≤
n
)
\mathbf K := (k(\mathbf x^{(i)}, \mathbf x^{(j)} + \tau^2\mathbf 1_{i=j})_{1 \leq i,j \leq n})
K:=(k(x(i),x(j)+τ21i=j)1≤i,j≤n)。当假设
y
i
=
f
(
x
i
+
ε
i
)
y_i = f(\mathbf x^{i} + \varepsilon_i)
yi=f(xi+εi), 且
ε
i
=
N
(
0
,
τ
2
)
\varepsilon_i = \mathcal N(0, \tau^2)
εi=N(0,τ2) 时,
τ
2
\tau^2
τ2 是噪声超参数。
通常,先验平均函数 μ μ μ 被选择为零 (在观察到y居中之后): GP的重点是定义和利用空间协方差。然而,拥有不同的 μ μ μ 肯定是有用的。如果已知目标函数是不平稳的,则添加多项式趋势项可能是一种解决此问题的方法。但是,如果不知道适当的趋势,则在使用高维度时要谨慎,因为很容易意外地推断出相当严重和有害的情况。稀疏趋势选择可能更可取,例如,由Kersaudy等人 [2015] 结合多项式混沌展开,如可能使用通过交叉验证 [Liang等人.2014] 或贝叶斯框架 [Joseph等人.2008] 提供的基础元素。
协方差函数族的选择决定了GP的定性性质。当然,我们要确保当我们完成将核函数应用于我们所有的数据时,得出的协方差矩阵是半正定的。保证这一点的函数本身称为半正定。通常将注意力进一步限制在平稳内核上,其中内核函数 k k k 是 x − x ′ x − x' x−x′ 的函数, k ( x , x ′ ) = k ∼ ( x − x ′ ) k(x,x') = \mathop {k}\limits^{\sim}(x − x') k(x,x′)=k∼(x−x′)。在此类中,最流行的内核可能是乘积形式的平方指数内核, k ( x , x ′ ) = σ 2 Π i = 1 d e x p ( − ( x i − x i ′ ) 2 2 θ i ) k(\mathbf x, \mathbf x') = \sigma^2 \Pi^{d}_{i=1}\ exp(-\frac {(x_i - x_i')^2} {2\theta_i}) k(x,x′)=σ2Πi=1d exp(−2θi(xi−xi′)2)。此核函数仅定义为其自由参数 θ 1 , . . . , θ d θ_1,...,θ_d θ1,...,θd,长度标度 (确定点之间的距离协方差开始下降) 和 σ 2 σ^2 σ2,后者根据 y y y 的比例将相关性转换为协方差。该内核诱导了一个无限可微的元模型,这可能是可取的,也可能不是可取的,这取决于与我们对黑盒的理解匹配的程度。为了精确控制可微性,请考虑由平滑度参数 ν ν ν 索引的 Matérn 类,该参数是根据第二种修改的 Bessel 函数定义的 (虽然当 ν + 0.5 ν + 0.5 ν+0.5是整数时,可以用简单函数来写)。有关 Matérn 和其他协方差函数类的更多信息,请参见Rasmussen和Williams。这样的GPs可以在最多 ν − 0.5 ν - 0.5 ν−0.5 的时间被区分。
在高维度上,GPs对点之间距离的这种依赖性是有问题的。因此,我们在本文中回顾的许多方法将不在原始输入空间上定义内核函数,而是在其某些转换上定义内核函数。 当然,可以将变换及其上的核函数一起视为新颖的核函数。但是,我们将在本文中采用分离降维转换和随后的纯基于距离的内核的观点,因为我们认为这种模块化有助于模型设计和比较。
就高斯过程而言,它是多元高斯分布的无限维推广,它保留了许多推动高斯性突出的分析特性。对我们特别有用的是对某些超出概率和相关指标的封闭形式评估,这些评估构成了将这些高斯过程部署到优化问题的基础。
关于GP回归的更多细节,我们参考Gramacy [2020] 和Rasmussen和Williams [2006],并且例如参考Kanagawa等人 [2018] 讨论与其他内核方法的连接。
2.2 贝叶斯优化
用Jones等人的有效全局优化方法推广,贝叶斯优化,参见,例如,Mockus等人,依赖于基于一些初始观测得的 f f f 的GP概率先验,来定义获取函数 α : X → R α: \mathcal X → \mathbb R α:X→R。这在以后进行了优化,以选择新的点进行顺序评估。初始阶段,称为实验设计 (DoE),通常通过评估基于优化的 Latin 超立方体样本的设计开始,其空间填充属性。算法1中给出了一个伪代码。

预期的改进和置信上限标准通常由于其在值和梯度上的分析可处理性而被使用。其他选择也是可能的; 例如,Shahriari等人 [2016b]。通用获取函数优化问题为
f
i
n
d
x
∗
∈
a
r
g
m
a
x
x
∈
X
α
(
x
)
(2)
find\ \mathbf x^* \in \mathop {argmax} \limits_{x \in \mathcal X} \alpha(\mathbf x) \tag{2}
find x∗∈x∈Xargmaxα(x)(2)
一些获取函数在黑盒有噪声的情况下是局部合适的,而一些需要像EI那样的适应; 参见例如Letham等人的讨论。少量噪声可能对其正则化效果有益,例如,参见Gramacy和Lee [2012],但是随着信噪比下降,寻找解决方案的努力急剧增加。更不用说输入变化和非高斯噪声,即使在低维中也很难处理。我们参考Forrester等人 [2008] 、Garnett [2022] 、Gramacy [2020] 和Roustant等人 [2012] 了解如何在实践中应用BO的更多细节。

图2. 距离集中在高维: 根据
[
0
,
1
]
d
[0,1]^d
[0,1]d 中的均匀度量随机采样10,000个点,然后计算平方点间距离,表明这些集中在高维可能值的范围内: [0,d]。
2.3 维度的诅咒及其影响
在距离计算 中首先感觉到输入维度的增加,这是最常见的协方差内核的核心。困难在于点在高维中相对较远,因此使用基于距离的协方差学习变得更加困难。除各向同性内核外,第二个影响是模型超参数数量的增加 ,通常使用许多长度尺度参数来调整协方差内核。因此,最大化 (非凸) 可能性变得越来越困难,因为维数的诅咒也会影响通常使用的基于梯度的优化例程。
同样,在高维中,精确优化获取函数 是复杂的,特别是因为它是具有平坦区域的多模态优化任务。此外,鉴于大部分体积都在域的边界上,并且基于GP的预测方差随着到设计的距离而增加(至少在低维中是一个理想的属性)缺点是,通常在d维超立方体的许多顶点或侧面之一上找到最佳,将平衡转向盲目探索。
当随机抽样时,维数的诅咒也会显现出来,这是某些积分量的 Monte Carlo 估计所必需的,其中包括熵,后验实现的优化点 (如汤普森抽样所要求的那样) 以及某些全局灵敏度度量。问题是,随着尺寸的增加,平均而言,均匀采样点 将越来越远离任何给定点。因此,挑战不仅在于在建模精度方面进行扩展,而且还在于保持推理可管理并避免获取函数优化中的陷阱。
3 高维高斯过程建模
结构模型假设 是避免建模中维度的指数依赖性的唯一方法,为此总结了各种选择,例如巴赫 [2017],他也给出了相应的泛化界限。正如我们接下来详细介绍的那样,这些不同的结构模型假设已经在GP上下文中进行了调整,以及其他假设。一个例外是使用各向同性内核,因此始终使用单个长度标尺,为此,尺寸的增加仅影响距离的行为。
3.1 变量选择或筛选
只要有可能,建议根据优化问题的专家知识限制变量数量。如果专家知识不可用,那么一个简单的、数据驱动的想法是在优化之前执行变量选择或筛选,例如,使用莫里斯技术或通过如Chen等人中的分层对角采样。其他全局敏感性分析技术 可用于单独选择变量,我们参考Iooss和lemaître [2015] 作为该主题的切入点。
因此,解决高维问题的早期尝试之一是假设大多数变量没有影响:
m
o
d
e
l
:
f
(
x
)
≈
g
(
x
I
)
w
i
t
h
I
⊂
{
1
,
.
.
.
,
d
}
,
∣
I
∣
≪
d
,
(3)
model:\ f(\mathbf x) \approx g(\mathbf x_I)\ with\ I \subset \{1,...,d\},|I| \ll d, \tag{3}
model: f(x)≈g(xI) with I⊂{1,...,d},∣I∣≪d,(3)
然后识别集合
I
I
I 中的那些有影响的变量。对于张量积形式的高斯核和其他平稳核,可以通过查看长度标度值来执行: 对于非常大的长度标度值 (如上参数化时),协方差的变化较小,其相应的输入变量可以因此被删除 。这在术语自动相关性确定 (ARD) 下也是已知的,如Rasmussen和Williams所讨论的。塞勒姆等人表明,这确实是渐近成立的。因此,我们的想法是根据变量的长度尺度对变量进行排名,以确定影响较小的变量。然后使用这些有影响的变量来构建GP模型并优化预期的改进。
然而, θ 1 > θ 2 θ_1 > θ_2 θ1>θ2 不一定意味着 x 1 x_1 x1 不如 x 2 x_2 x2 重要。因此,Linkletter等人 [2006] 建议在完全贝叶斯GP框架中比较对应于真实和人工添加的惰性变量的长度尺度的后验分布,而不是只看长度尺度值。Winkel等人中的局部变量选择补充了这一点,它依赖于忽略某些维度时所做的预测。Eriksson和Jankowiak [2021] 选择将马蹄形优先 [Carvalho等人2009] 放在逆长度尺度上,并执行基于梯度的数值后验模拟,从变量子集上定义的函数后验中取样。通过更渐进的方法,Marrel等人 [2008] 提出了基于Akaike信息准则 (分别为预测系数Q2) 向回归 (分别为协方差) 元素顺序添加变量。
Ulmasov等人没有明确决定保留哪些变量,这可能是耗时的。他们建议在每次迭代中采样一些变量,其中权重向量是通过主成分分析 (PCA) 在 ( x ) 1 ≤ i ≤ n (\mathbf x)_{1 ≤ i ≤ n} (x)1≤i≤n上确定的。如Li等人 [2017] 所示,这对于小预算可能不有效,他们更喜欢统一选择变量并填写剩余变量的值。
在实践中,大多数变量通常对输出的影响可能有限但非零。尽管这可能意味着选择要保留的变量的数量在某种程度上是任意的,但变量选择的简单性 (无论是实现还是解释) 都使其成为一种引人注目的降维方法,尤其是对于第一次通过。当然,变量选择本身只会随着维度的增加而变得更加困难,但这比下面讨论的一些更复杂的方法要小。尽管如此,该方法的优势也是其局限性,对于构成黑盒问题的复杂函数来说,真正而强烈地依赖于所有输入参数是很常见的。在所有变量都具有相同影响的情况下,无论关系多么简单,变量选择甚至都无法将维数减少一个。其他结构假设可以克服这些限制,并利用变量之间的相互作用。
3.2 加性模型和方差分析模型
一组可以保留所有变量但限制其相互作用的结构假设是可加性:
m
o
d
e
l
:
f
(
x
)
≈
μ
+
∑
i
=
1
d
g
i
(
x
i
)
,
(4)
model:\ f(\mathbf x) \approx \mu + \sum\limits_{i=1}^dg_i(x_i), \tag{4}
model: f(x)≈μ+i=1∑dgi(xi),(4)
具有单变量函数
g
i
g_i
gi。这已经被Durrande等人 、Duvenaud等人、Neal和Plate 转换到GP框架,最初是通过单变量核的求和:
k
(
x
,
x
′
)
=
∑
i
=
1
d
k
i
(
x
i
,
x
i
′
)
k(\mathbf x, \mathbf x') = \sum_{i=1}^{d} k_i (x_i,x_i')
k(x,x′)=∑i=1dki(xi,xi′),这就产生了一个有效的协方差函数,就像乘积形式一样。可解释性和可视化的一个有用性质是,GP预测均值可以分解为单变量分量之和:
m
n
(
x
)
=
k
(
x
)
T
K
−
1
y
=
∑
i
=
1
d
k
i
(
x
i
)
K
−
1
y
=
∑
i
=
1
d
m
n
,
i
(
x
i
)
m_n(\mathbf x) = \mathbf k(x)^T\mathbf K^{-1}\mathbf y = \sum^d_{i = 1}\mathbf k_i (x_i)\mathbf K^{−1}\mathbf y = \sum_{i=1}^dm_{n,i}(x_i)
mn(x)=k(x)TK−1y=∑i=1dki(xi)K−1y=∑i=1dmn,i(xi),与
k
i
(
x
i
)
:
=
(
k
i
(
x
i
,
x
i
(
j
)
)
)
1
≤
j
≤
n
\mathbf k_i(x_i ) := (k_i (x_i,x^{(j)}_i))_{1 ≤ j ≤ n}
ki(xi):=(ki(xi,xi(j)))1≤j≤n。更令人惊讶的性质是,由于不同观测之间出现的线性关系,协方差可以变得不可逆,这可以通过添加噪声项来减轻。因此,在未观察到的设计点处,预测方差可能为零,这对于探索和优化是一个有害的副作用。另一个困难是估计超参数,每个坐标需要额外的方差参数
σ
i
\sigma_i
σi (因此,超参数的数量大约增加一倍)。尽管如此,与高维值迅速变为零的张量积形式相比,总和形式的比例要好得多。Lin和Joseph [2020] 探索了通过应用输出变换来使黑盒更具添加剂。
高阶模型可以用相同的方式定义 [Duvenaud等人2011],通常限制为二阶或仅在所有低阶都已选择的情况下才选择高阶分量。相反,Plate建议在一阶交互的基础上一次添加所有交互。直接识别变量组也是可能的; 例如,Gardner等人 [2017] 、Kandasamy等人 [2015] 和Wang等人 [2018,2017]:
m
o
d
e
l
:
f
(
x
)
≈
μ
+
∑
i
=
1
M
g
i
(
x
A
i
)
(5)
model:\ f(\mathbf x) \approx \mu + \sum\limits_{i=1}^Mg_i(\mathbf x_{A_i}) \tag{5}
model: f(x)≈μ+i=1∑Mgi(xAi)(5)
多变量
g
i
g_i
gi 函数作用于 {1,…,d} 的
A
i
A_i
Ai不相交子集,使得
U
i
M
A
i
=
{
1
,
.
.
.
,
d
}
U_i^M A_i= \{1,...,d\}
UiMAi={1,...,d}。变量的不相交子集的限制在随后的工作中被进一步取消; 例如,参见Hoang等人 [2018] 和Rolland等人 [2018]。
它们的形式相似,但根植于全局灵敏度分析的是基于方差函数分析的加性模型 (fANOVA,也就是Sobol-Hoeffding) 分解 [Efron和Stein 1981; Sobol 2001]:
m
o
d
e
l
:
f
(
x
)
≈
c
+
∑
i
=
1
d
g
i
(
x
i
)
+
∑
j
<
k
g
j
k
(
x
j
,
x
k
)
+
⋅
⋅
⋅
+
g
12...
d
(
x
1
,
x
2
,
.
.
.
,
x
d
)
,
(6)
model:\ f(\mathcal x) \approx c + \sum\limits_{i=1}^dg_i(x_i) + \sum\limits_{j<k}g_{jk}(x_j, x_k) + ··· + g_{12...d}(x_1, x_2,...,x_d), \tag{6}
model: f(x)≈c+i=1∑dgi(xi)+j<k∑gjk(xj,xk)+⋅⋅⋅+g12...d(x1,x2,...,xd),(6)
具有基本函数
g
.
.
.
g...
g... 对于分解的唯一性,需要居中且正交。好处是可以进行敏感性分析,并将其解释为常规方差分析。Muehlenstaedt等人依靠这种分解直到二阶相互作用来建立他们的模型,根据出现在该公式中的sobol指数 (并由具有各向异性张量积核的第一遍GP估计) 来选择它们的分量。这些就是所谓的主效应 (只有一个变量) 和总相互作用效应 (两个变量在任意顺序上的效应)。选择要删除的交互以形成集团需要阈值方案。Ulaganathan等人提出了一种类似的方法,当梯度观测可用时,增加切点。Durrande等人进一步使用专用内核,其形式为
k
A
N
O
V
A
(
x
,
x
′
)
=
Π
i
=
1
D
(
1
k
i
(
x
i
,
x
i
′
)
)
k_{ANOVA}(\mathbf x,\mathbf x') = \Pi ^ D_{i=1}(1 k^i(x_i,x_i'))
kANOVA(x,x′)=Πi=1D(1ki(xi,xi′)) ,如Stitson等人。在那里,方差分析表示的灵敏度指数是可分析的。在Ginsbourger等人中,方差分析分解直接在核上进行,并在适当的正交性条件下传播到相应的随机场。寻找稀疏性以避免估计整个
2
d
2^d
2d分量,他们定义了投影仪,该投影仪允许将加法分量 (主效应之间具有互协方差) 与补体分开。
这些技术的主要缺点是,在这种情况下,推理具有挑战性,其中包括许多术语。因此,已经应用了各种估计超参数的技术: 类似坐标上升的 [Durrande等2012] 或准牛顿 [Duvenaud等2011] 似然最大化方法。依赖随机性有时更倾向于绕过完全优化的成本,比如Kandasamy等人 [2015],其中随机分解被采样,并选择最佳的可能性 (固定术语的顺序和数量),或者Wang等人 [2018]。加德纳塔尔[2017] 试图通过专用的metropolis hastings算法引出该结构。对于重叠的子集,Hoang等人 [2018] 也依赖于随机组,而Rolland等人 [2018] 使用依赖图和Gibbs采样来执行推断。在这种方法中,Delbridge等人 [2020] 根据地统计学 [Journel 1974] 的转向带方法的精神,通过随机方向上的变量和重建高维核。
然而,就优点而言,该方法保持了变量选择的可解释性,特别是如果所选模型主要包括一阶或二阶项并且有些稀疏。通过观察通过推断的过程选择哪些对来学习哪些变量相互作用本身在科学上是很有趣的。
有些作品也致力于扩展到许多观察结果,例如Mutny和Krause [2018],具有GP内核的基础扩展。Sung等人 [2020] 还提出了基扩展,进一步用具有群lasso估计程序的多分辨率方案对其进行了补充。Wang等 [2018] 用随机分割的输入空间、随机加性近似和随机特征分解的核对许多观测进行尺度。
在这里,一个基本假设是高阶相互作用成分可以忽略不计 (因为在这种形式主义中很难估计),尽管这是实验设计中的悠久传统。另一个担忧是方差分析无法检测非线性和多模态 [Palar和Shimoyama 2017]。这些缺点通过以下框架得到缓解。
3.3 线性嵌入
设计高维内核的一种方法是避免直接这样做,而是首先通过降维图运行数据。这些数据在此映射下的图像称为其嵌入,用于降维的一个明显的函数类是线性函数类。实际上,正如Marcy [2018] 所指出的那样,使用线性映射的想法至少可以追溯到Matérn [1960]。然后,问题是要特别使用哪个线性函数。
用
z
=
A
x
\mathbf {z = Ax}
z=Ax 表示此通用映射,其中
A
∈
R
r
×
d
\mathbf A \in \mathbb R^{r\times d}
A∈Rr×d。在Vivarelli和Williams的情况下,
r
=
d
r = d
r=d,因此映射用于旋转空间而不是实际减小尺寸,但是我们对
r
≪
d
r \ll d
r≪d 情况更感兴趣。当
r
=
1
r = 1
r=1 时,这是一种流行的降维技术,称为单索引模型:
m
o
d
e
l
:
f
(
x
)
≈
g
(
a
T
x
)
w
i
t
h
a
∈
R
d
(7)
model:\ f(\mathbf x) \approx g(\mathbf a^T\mathbf x)\ with \mathbf a \in \mathbb R^d \tag{7}
model: f(x)≈g(aTx) witha∈Rd(7)
我们将Gramacy和Lian用于GP处理,将
a
\mathbf a
a 视为附加的核超参数。正如Kirschner等人所建议的那样,可以在每次迭代中简单地随机选择
a
\mathbf a
a。不幸的是,扩展到
r
>
1
r > 1
r>1 绝非易事。假设是
m
o
d
e
l
:
f
(
x
)
≈
g
(
A
T
x
)
(8)
model: f(\mathbf x) \approx g(\mathbf A^T\mathbf x) \tag{8}
model:f(x)≈g(ATx)(8)
其中此类函数在文献中称为岭函数。它与观察结果相对应,有时得到理论证据的支持,高维函数的变化可以集中在几个但未知的方向上。有几种选择
A
A
A 的方法,我们将依次回顾。
对于GP回归,可以说最直接的方法是简单地将 A A A 视为另一个要学习的核超参数,例如,通过边际似然优化。固定r,Garnett等人 [2014] 提供了一个近似贝叶斯方案来做到这一点,其具有对可能性的拉普拉斯近似,随后是对超参数的近似边缘化。Tripathy 等人 [2016] 依赖于一个两阶段的方法:首先使用可能性来学习正交 A A A ,然后找到其余的超参数(并重复)。BIC用于确定参数 r r r 。正交性约束需要一些特殊考虑,因为这些矩阵位于Stiefel流形上。Seshadri 等人[2019] 重新解释了一个类似的问题,在回归和近似之间建立了联系。还建立在Tripathy等人[2016] 和Yenicelik [2020] 的基础上,观察到可能性可能并不总是在替代方案中选择最佳矩阵。Marcy [2018] 提出了一个完整的贝叶斯处理,它具有矩阵流形和维度的先验,需要先进的蒙特卡罗方法。
运行独立于GP模型的灵敏度分析以选择 A A A 作为一种预处理步骤也是一种选择。当黑盒的梯度可用时,恢复矩阵A相对简单。直到旋转,它对应于矩阵 C : = ∫ X ∇ ( f ( x ) ) T ∇ ( f ( x ) ) λ ( d x ) C := \int_{\mathcal X}\nabla(f(\mathbf x))^T\nabla(f(\mathbf x)) \lambda(d\mathbf x) C:=∫X∇(f(x))T∇(f(x))λ(dx) 具有非零特征值的特征向量,其中 λ λ λ 是设计空间上的任何行为良好的度量 (通常是超立方域上的Lebesgue)。然后可以使用蒙特卡洛估计器。放宽某些特征值恰好为零的假设,得到了主动子空间(AS)方法[Contantiny2015],进行了降维和可视化分析。特别是, C C C 的特征值的间隙暗示了AS的存在。如果可以评估梯度,那么这是GP建模前的一个很好的预处理步骤。如果没有梯度信息,有限差分通常代价太高,因此使用GP来估计 C C C 可能更合适,例如,在Fukumizu和Leng [2014]和Palar和石山[2017]中。Djornga等人[2013]使用具有有限差分的方向导数来恢复BO之前具有低秩矩阵恢复的A。可以使用其他压缩传感技术,最初由Carpentier和Munos [2012] 完成,后来由Groves和Pyzer-Knapp [2018] 完成。由于设计点的独立同分布假设,A 的 MC 估计量以两阶段方法应用。Wycoff等[2021] 表明,对于标准固定内核,GP的C矩阵的估计是可处理的,从而减轻了对该采样假设的需求。对切片逆回归或偏最小二乘法进行敏感性分析以恢复 A 并可能在优化期间对其进行更新的其他工作。Lee[2019]主张采用修正的AS矩阵,夸大了平均梯度的影响(在输入空间上)。
最后,与其把学习 A A A 作为GP超参数推理的一部分或作为敏感性分析的结果,第三种选择是简单地随机选择 A A A,要么在建模步骤之前生成一个单一的 A A A 矩阵,要么使用不同的 A A A,例如在每个迭代中。 例如,在随机嵌入BO(REMBO) 中,Wangetal[2016,2013] 使用固定且随机采样的 A A A 。一种理由是由于Johnson-Lindenstrauss引理而导致的L2范数的随机投影的稳定性,例如,由Letham等人 [2020] 注意到。在BO的背景下,其理由是,至少对于无界域来说,在低维嵌入上存在问题的解决方案,解释了随机优化[Bergstra和Bengio 2012]在一些超参数调整问题上的成功。
即使有了候选 A A A ,无论是通过优化、敏感性分析,还是随机抽样,我们仍然要做出建模决定(更不用说获取决定;第4.3节)。看似无害的超立方体域的选择在与线性降维相结合时可能会让人头痛,因为可能的解空间不再是简单的立方体,而是由 A A A 定义的多角形。如果我们的GP适合于低维空间,那么它可能更容易找到下一个候选点进行优化,但我们必须弄清楚原始空间中的哪一个点对应于这个低维的最优。这意味着不仅预像不是唯一的,而且点的反投影甚至不能保证存在于原始单位超立方体中,并且可能需要凸投影才能恢复可行性。这意味着我们的反投影不再是线性的。Wang等人[2013]提出的补救方案是忽略相应的非注入性问题,或者使用定义在X上的核,失去低维GP建模的好处。Binois等人[2015]提出在Y中加入高维信息的翘曲来解决非注入性问题,而Binois等人[2020]定义了一个从Y到X的替代映射来避免这个问题。Nayebi等人[2019]也通过选择一个只有{-1, 0, 1}元素的稀疏随机矩阵来绕过这个问题,实质上是从超立方体的对角线上选择嵌入。 这些想法可以扩展到仿射嵌入,如Cartis等人 [2020] 和Cartis和Otemissov [2021] 提出的全局优化。
然后是如何使用非线性嵌入的高维数据的问题(与 REMBO 不同)。除非A完全恢复,否则必须引入噪声项以解决差异。为此,Moriconi等人[2020]使用GP回归对轴对齐的投影进行定量分析。 另一个问题是在这种情况下如何选择长度尺度,因为乘积核在嵌入空间中不被保留,对此Letham等人[2020]表明一个特定的参数化(基于Mahalanobis距离的核)是比较好的,可以避免失真。尽管如此,推论仍然很复杂,而REMBO程序只需要拟合一个低维的GP。Binois[2015]、Binois等人[2020]和Letham等人[2020]也简要研究了从什么分布中取样A。
尽管在一般情况下,任何GP都可以在缩小的空间中拟合,但与加性假设的联系是自然的,Gilboa等人[2013]以投影-追求的方式结合这些,导致了投影加性近似。在这种情况下,调整 r r r 参数是通过迭代增加维度,并在精度停止增加时停止。Li等人[2016]进一步讨论了在一个受限的投影追求设置中,如何将这种方法扩展到优化。这可以被看作是介于拟合一个完整的低维模型和使用一阶加性模型之间。这些想法可以通过估计几个低维子空间结合起来;例如,见Wongetal. [2020]和Yenicelik[2020]。
在使用线性嵌入(一般来说,它有 p × r p\times r p×r个参数)时,估计的风险很强,有未解决的问题: (i) 矩阵A必须学习得多好,才能比直接拟合高维问题更好?(ii) 应将多少预算专门用于这项任务?(iii) 什么时候动态地学习A,导致一个有噪声的GP(只要设计点不都在REMBO的同一嵌入上)会更好?另外,除非有专家信息,否则找到一个合适的r仍然很困难。幸运的是,采取大于必要的值并无害处–只是它很快就会重新带来高维的挑战[Cartis和Otemissov 2021;Wangetal. 2013]。
线性嵌入方法已经放弃了选择和方差分析方法所提供的大部分可解释性(当我们在下一节考虑非线性嵌入时,情况会变得更糟)。在 r ∈ { 1 , 2 } r \in \{1,2\} r∈{1,2} 的情况下,有可能创建函数的可视化,这可能是直觉的巨大来源。但在大维度的情况下,我们就只能眯着眼睛看每个变量在保留方向上的负荷。然而,与轴对齐的变量选择相比,确实有一些函数在使用线性嵌入时可以被减少到更小的维度。这两种方法中哪一种会更合适是根据问题所定的。
3.4 非线性嵌入和结构化空间
放弃线性假设为模型增加了更多的灵活性,但代价是需要更多的数据来拟合它。当数据处于低维流形时,Guhaniyogi和Dunson[2016]等人提出了恢复这样一个适合回归的流形。将线性降维扩展到非线性情况的一个简单方法是使用局部线性方法,正如Wycoff[2021b]在AS的背景下所做的那样。与AS类比定义的还有Bridges等人[2019]的一维主动流形,还没有应用于GPs。在这一思路中,还可以包括生成性地形图[Viswanath等人,2011]、GP潜在变量模型,例如Lawrence[2005]和Titsias和Lawrence[2010],或深度GP[Damianou和Lawrence 2013;Hebbal等人,2019;Sauer等人,2020]。深度高斯过程指的是假设输入通过一连串的高斯过程与输出相联系的建模策略,一个过程的输出作为下一个过程的输入。 这不能与深度内核的概念相混淆[Huang等人,2015;Wilsonetal.2016],后者只涉及一个高斯过程,但其内核函数是由神经网络参数化的。通常,推理是通过优化(估计)对数边际似然对GP和神经网络权重进行的,但在结构化输入或部分标签的情况下,神经网络可以被初始化为一个自动编码器(即初始化为重建输入)。一个避免较大优化预算的正交方向是通过多保真度,当有更便宜但不太精确的黑箱版本时,例如Falkner等人[2018]和Ginsbourger等人[2013]就利用了这一点。
在这种情况下,这些高度灵活的模型可能更容易被接受,即关于问题结构的一些额外信息是可用的。其中一种情况是几何形状的优化,通常是翼型。Lukaczyk等人[2014]在这种情况下进行了AS。由于有许多选项可以对这些形状进行参数化,有些更适合于优化。独立于这种选择,Gaudrie等人[2020]建议在形状空间中工作,用形状特征向量和它们的值来定义,这并不昂贵,因为一般来说,几何形状的计算在随后的模拟中是可以忽略的。Chen等人[2020a]使用了形状基础的非线性计算,生成式对抗网络被用来从真实数据中学习流形。
一个相关的方法使用变异自动编码器[Kingma和Welling 2013]作为深度内核[Gómez-Bombarelli等人2018],确保高斯过程应用其内核的潜在状态可以近似恢复原始的、未编码的输入。当对结构化的非欧几里得输入进行优化时,这种方法很受欢迎,例如分子[Deshwal和Doppa 2021; Eismann等人2018; Grosnit等人2021; Gómez-Bombarelli等人2018;Mausetal. 2022;Tripp等人,2020],对于这些标准的BO是不可用的。其他关于图上索引的功能数据的例子包括[Espinasse等人,2014]。
Jaquier和Rozo[2020]在黎曼尼流形上为机器人进行几何感知的BO,将第3.3节的一些想法移植到非欧几里得空间。Oh等人[2018]的一个有点相关的假设是使用圆柱坐标而不是原来的直角坐标(而不是像Padonou和Roustant[2016]那样使用极坐标,因为极坐标的尺度不大)。基本假设是,如果选择合适的话,解决方案靠近域的中心。变换坐标相当于分离了径向和角度部分:
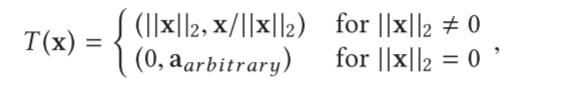
而逆变换是
T
−
1
(
r
,
a
)
=
r
a
T^{-1}(r, \mathbf a) = r\mathbf a
T−1(r,a)=ra 。对应的协方差核为
k
c
y
l
(
x
,
x
′
)
=
k
r
(
r
,
r
′
)
×
k
a
(
a
,
a
′
)
k_{cyl}(\mathbf x, \mathbf x') = k_r(r, r') \times k_a(\mathbf a, \mathbf a')
kcyl(x,x′)=kr(r,r′)×ka(a,a′)。选择一维半径分量
k
r
(
r
,
r
′
)
=
k
(
∣
(
1
−
r
α
)
β
−
(
1
−
r
′
α
)
β
∣
)
k_r(r, r') = k(|(1 - r^\alpha)^\beta - (1 - r'^\alpha)^\beta|)
kr(r,r′)=k(∣(1−rα)β−(1−r′α)β∣) ,
α
,
β
>
0
α, β > 0
α,β>0,以进一步聚焦于中心[Oh et al. 2018],而角度分量是一个连续的径向核
K
a
(
a
,
a
′
)
=
∑
p
=
0
P
c
p
(
a
T
a
′
)
p
,
c
p
>
0
,
∀
p
K_a(\mathbf a, \mathbf a') = \sum_{p=0}^Pc_p(\mathbf a^T\mathbf a')^p, cp > 0, ∀p
Ka(a,a′)=∑p=0Pcp(aTa′)p,cp>0,∀p, 用户定义p。
非线性方法在高维度上取得了巨大的成功,特别是当空间是结构化/非欧几里得时。然而,这是以增加复杂性为代价的,包括计算(例如,当使用深度神经网络时)和解释。因此,我们的建议是将这些技术保留给最棘手的问题,并考虑更简单的解决方案,特别是如果希望洞察功能,而不仅仅是一个最佳解决方案。
要在高维度上构建一个令人满意的GP模型,有很多圈套和障碍。然而,这只是走了一半的路,因为还需要优化获取函数。
4 高维获取函数优化
提出的高维GP模型通常与获取函数优化的策略相结合,以适应特定的模型结构和维度的诅咒。许多这些方法可以从它们被提出的建模框架中解脱出来,留下许多可能的组合没有被探索。我们现在根据它们本身的优点来讨论它们。
更快的评估时间和梯度的可用性为全局优化多模态获取函数提供了有限的帮助。全局优化的保证是遥不可及的,因为分支和边界方法或DIRECT不能扩展[Jones等人,1998]。除了局部最小值外,另一个缺陷是存在大的高原,即采集函数值是平坦的,而局部最优值可能是峰值。 为了减少这两种影响,Rana等人[2017]建议在各向同性的GP中采取较大的长度尺度来人为地扩大梯度。然后,在跟踪后续的最优值(由之前的值开始的温暖)时,连续减少长度标度。Tran-The等人[2019]在获取函数优化的层面上应用了REMBO的随机线性嵌入(第3.3节),在有限的子空间集合上进行优化。
无论拟合的GP模型的质量如何,作为变量数量的函数,不断扩大的边界体积对采集的优化有很大影响(公式(2))。如果基于均匀取样,例如采用多起点梯度优化甚至进化算法,那么搜索将集中在这些边界区域。边界上较大的方差会使获取函数的最优位置在那里得到加强,在关注内部之前,没有希望评估所有的面或顶点。在评论和讨论这些影响时,Oh等人[2018]提出使用圆柱坐标与BOCK来提高内部体积的权重,传授最佳状态接近中心的预先知识。像Siivola等人[2018]那样在边界上增加虚拟导数观测在高维度上几乎是不可行的,因为导数信息只在GPs中有限的几个配位点上可以分析执行(实际上计算量在相同的情况下是立体扩展的)。无限的版本有可能通过谱系方法来实现,例如基于Gauthier和Bay[2012]。在这种情况下,使用信任区域(TR)可以极大地限制搜索空间的大小。信任区域方法将优化集中在当前最佳解决方案(TR中心)的邻域内,如果新的候选点比TR中心有足够的改善,那么TR中心的大小就会增加,反之就会减少;例如,见Larson等人[2019]的观点。结合BO,这已被证明在高维度 [Daulton等人。2021; Diouane等人。2021; Eriksson等人。2019; Regis 2016; Zhou等人。2021],也许是以不太全局的搜索为代价 (可能通过重新启动或并行TR来补偿)。为了进一步避免TR边界的吸引,等式(2) 仅在Eriksson等人 [2018] 中的离散集合上进行优化,其中一些坐标随机保留在TR中心。
虽然上述策略主要独立于GP模型 (例如,与各向同性或各向异性产品内核一起使用),但我们接下来详细介绍了具有结构假设的GPs策略。请注意,这些假设在实践中从未完美地实现或估计过,需要引入噪声分量来说明引入的近似值,只有少数例外。因此,在等式 (2) 的优化中必须考虑这一点。
4.1 Additive Case
可加性提供了依靠与GP相同的分解来求解方程 (2) 的机会,因此将搜索减少到可能并行的几个低维搜索。也就是说,与其关注 f f f 的后验,不如关注那些加性成分,即模型(4,5,6)中的 g i g_i gi: N ( m n , i ( x I ) , s n , i 2 ( x I ) ) \mathcal N(m_{n, i}(\mathbf x_I), s^2_{n,i} (\mathbf x_I)) N(mn,i(xI),sn,i2(xI)),其中 s n , i 2 ( x I ) = k i ( x I , x I ) − k i ( x i ) T K − 1 k i ( x i ) s^2_{n,i}(\mathbf x_I) = k_i (\mathbf x_I, \mathbf x_I) − \mathbf k_i (\mathbf x_i )^T\mathbf K^{−1}\mathbf k_i (\mathbf x_i ) sn,i2(xI)=ki(xI,xI)−ki(xi)TK−1ki(xi)对于一般下标 I I I 。然后在每个 g i g_i gi 模型上定义部分获取函数,作为一个总和,例如在Kandasamy等人[2015]。对于重叠的子集需要更加谨慎,比如说依靠消息传递[Hoang等人,2018;Rolland等人,2018],但它仍然比在原始空间中优化更有效率。这种方法的主要优点是,它允许解决 d d d 个许多一维优化问题,而不是一个d维问题,在非凸的情况下,这等于是容易很多倍。尽管如此,使用加性模型在未观察到的位置处的零方差在多大程度上影响搜索的全局性仍然未知。添加内核一个组件,有助于减轻错误的假设,如变量选择或如下,可能是有趣的。对于高维挑战传统采集功能优化且预算足够小以至于我们无法期望学习该功能的高保真表示的问题,应考虑加法GPs。
4.2 变量选择
如果在初步阶段事先将变量完全删除,那么就可以使用一个固定的值,回到低维问题。具有其他值的观测值一般被丢弃,以保持问题的确定性,如果惰性变量可以变化,则可选择添加一些噪声。否则,在对少数变量进行优化方程(2)后,必须确定被筛选的变量的值来评估f。备选方案包括将这些变量固定为一个常数,在这些坐标的最佳设计采样处取值,随机采样,或这些的组合;例如,见Spagnol等人[2019]和Li等人[2017]。在Salem等人[2018]中,通过寻找仍能通过似然比测试的最不同的值来估计其余变量的替代长度标度。然后,在两组超参数之间预测平均值差异最大的地方选择这些变量的值,以挑战初始分裂。
在考虑获取函数时,变量选择方法的主要优点是减少了搜索空间的维数,从而减轻了获取优化的负担。但是,该问题不会像在加法情况下那样分解,而且可能会对 "不活动 "的变量使用次优的值。
4.3 Embedding Case
在嵌入方面,有界域会产生额外的困难。令
W
=
[
A
W
2
]
\mathbf {W = [AW_2]}
W=[AW2] 为
R
d
\mathbb R^d
Rd 的基础。在活跃和不活跃(或不太活跃)的变量之间进行分割:
∀
x
∈
R
d
,
x
=
W
W
T
x
=
A
A
T
x
+
W
2
W
2
T
x
=
A
y
+
W
2
z
,
y
∈
R
r
,
z
∈
R
d
−
r
\forall \mathbf x \in \mathbb R^d, \mathbf x = \mathbf W \mathbf W^T\mathbf x = \mathbf {AA^Tx + W_2W_2^Tx} = \mathbf {Ay} + \mathbf {W_2z}, \mathbf y \in \mathbb R^r, \mathbf z \in \mathbb R^{d-r}
∀x∈Rd,x=WWTx=AATx+W2W2Tx=Ay+W2z,y∈Rr,z∈Rd−r。.如果
f
f
f 有一个真正的活动子空间,那么问题就变成了
f
i
n
d
y
∗
∈
a
r
g
m
i
n
y
∈
y
⊆
R
r
f
(
p
X
(
A
y
)
)
(9)
find\ \mathbf y^* \in \mathop {argmin}\limits_{\mathbf y \in y \subseteq \mathbb R^r} f(p_{\mathcal X}(\mathbf {Ay})) \tag 9
find y∗∈y∈y⊆Rrargminf(pX(Ay))(9)
用
p
X
p_{\mathcal X}
pX 表示在
X
\mathcal X
X 上的凸投影;否则,问题是
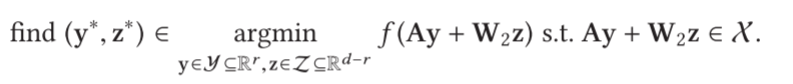
正如君士坦丁 [2015] 所讨论的,也许 z z z 上的优化是次要的,可以重写为

其中可以在解决涉及 z z z 的高维子问题上投入较少的精力。这可以通过随机抽样进行[Constantine 2015]。另外,我们也可以从变量选择的优化中吸取经验,固定不活动的方向;例如,见Cartis等人的文章。对于无界域是无害的,对于紧凑域 X \mathcal X X,属于评估域的约束很复杂。每当 A A A 在迭代过程中发生变化时,由于需要在嵌入中投影设计点 (即,当存在 z z z 分量但在 f f f 的建模中被忽略时),优化问题就会产生噪声。
仅讨论(居中的) [ − 1 , 1 ] d [-1, 1]^d [−1,1]d 超立方体的情况,与线性嵌入的交点是一个凸多面体,定义为 Y = { y ∈ R r s . t . − 1 ≤ A y ≤ 1 } \mathcal Y = \{\mathbf y \in \mathbb R^r\ s.t. - 1 ≤ \mathbf{Ay} ≤ 1\} Y={y∈Rr s.t.−1≤Ay≤1}。 这是Letham等人[2020]主张的解决方程(9)的域,在优化 α \alpha α 时需要处理线性约束的额外成本。对于随机 A \mathbf A A,更简单的选择是在超立方域 Y = [ − l , l ] r \mathcal Y=[-l,l]^r Y=[−l,l]r内优化 y \mathbf y y, l l l 的选择基于找到解决方案的概率,如Cartis等人[2020]、Qian等人[2016]和Wang等人[2016,2013]中所衍生的。如果真正的活动子空间是轴对齐的,则这些结果会更简单,并且取决于 r r r 和真正的低维(如果存在)之间的差异。尽管如此, Y \mathcal Y Y 的这些选择甚至可能不包含 y ∗ \mathbf y^* y∗。最小的紧凑集是 Binois 等人描述的星形多边形。 [2020]。关注较小 Y \mathcal Y Y 的原因有两个。 首先,大部分的差异对应于 X \mathcal X X 的边界上的点,与交点相比,体积越来越大,又带来了维度的诅咒。第二,相应的观测值被凸投影扭曲了,因此更难建模。Moriconi等人[2020]和Nayebi等人[2019]以更严格的对角线或轴对齐的嵌入假设为代价绕过了这些问题。改变领域,正如选择 l l l 所隐含的那样,涉及到另一个在BO中没有过多探讨的策略:减少优化空间或采用TR的方式。
Raponi等人提出了 A A A 的加权PCA估计。[2020],它们处理域问题时会因不可行而受到惩罚。Chen等人 [2020b] 使用半监督版本的切片逆回归 (SIR) 来寻找重要的输入方向,同时使用标记 (评估) 和未标记 (未评估) 设计。也就是说,它们收集具有高采集函数值但未被选择用于评估的点到 “未标记数据集” 中,它们将其合并到嵌入的估计中。SIR中的 “逆” 表示交换 x \mathbf x x 和 y y y 的作用的目标,找出设计的哪些值导致输出的给定值。选择域会遇到与上述相同的困难,以及与更新SIR模型相关的困难。
大多数现有的工作固定了嵌入,或者在迭代估计时不传播不确定性。探索在AS函数上定义的获取函数(如Garnett等人[2014]和Wycoff[2021b])与为优化而定义的获取函数之间的相互作用,是增强两者的一个有希望的方向。
因此,当涉及到嵌入时,它们往往使获取函数的搜索复杂化而不是简单化。当存在足够的评估预算来学习嵌入时,这仍然值得付出额外的努力。
如Siivola等人[2021]所示,这些领域选择的问题在非线性降维中被放大。Li等人[2016]同时面临可加性和嵌入问题,限制了投影项的范围,使其主要停留在域内。接下来,我们提供基准问题的指针,以凭经验评估上面详述的各种方法。
5 综合测试优化问题
由于可能的方法和组合的多样性,全面的经验比较不在本工作范围内。此外,实现方式并不总是可用的,甚至是兼容的。推理技术也可能有所不同,使比较复杂化。一个不太明显的困难是缺乏用于基于高维代理的优化的标准基准函数。因此,我们在这里列出了我们遇到的选项。
首先,来自全局优化的一些标准基准函数,例如inHansen等人 [2021],可以扩展到高维。这些综合测试函数可以分为可分离的、具有中等(分别为高)条件的单峰函数,最后是具有全局结构的多峰函数。正如Diouane等人所说,只有最后一个是在BO领域。但是,即使是这样的问题也往往是病态的,例如,随着 d d d 的增加,局部最优点的数量呈指数级增长,因此无论可以多快评估模拟器,都需要比合理地提供更大的预算来找到全局解决方案。在有限的预算下为这些可扩展的问题定义合理的、次全局的最佳目标可能是一种选择。附录表 3 列举了这些全局优化函数。 Siivola 等人测试了为 BO 创建的其他内容[2018]。https://www.sfu.ca/ssurjano/optimization.html 中的五个物理驱动分析函数也是 BO 基准测试的主题:钻孔 (8 d d d)、OTL 电路 (6 d d d)、活塞 (7 d d d)、机械臂 ( 8 d d d)和翼重(10 d d d)。电源电路函数 (13 d d d)[Lee 2019] 又举了一个这样的例子。几个为敏感性分析而设计的函数也被试验过:Sobol g-function(任意d),Ishigami函数(3d),以及Iooss和Lemaître[2015]的8d洪水模型。评估这些分析实例与结构模型假设的充分性是未来有趣的工作。
另一种选择是将人工的、不活跃的变量添加到经典的低维测试函数中,使问题名义上是高维的,但本质上是低维的。虽然这很容易扩展到数十亿的变量,如Wang等人[2013],但它可能并不现实。这些低维玩具函数的重复版本也被提出,例如,Oh等人[2018]。这种方法只是把同一函数的许多低维版本加在一起,允许有更多的活动变量。另一个选择是通过线性变换来旋转低维函数,但有两个问题:初始超立方域可能不会填满整个高维域,或者部分区域可能被映射到外面,包括已知的最优值。分析函数可以很容易地扩展以填补空白,但问题的难度变得与旋转有关。为了便于比较,可以使用一组固定的旋转,或者像Nayebi等人[2019]提出的一类嵌入矩阵,不存在相同的领域问题。

GP实现是测试给定结构的估计难度的一个简单选择,也可用于结构之间的比较,如Ginsbourger等人[2016]。这些结果在多大程度上适用于实际应用仍然是一个研究课题。为此,表 1 提供了可以使用公开可用软件重现的问题列表。其中一些问题来自于机器学习界流行的超参数调整应用,包括用BO调整各种神经网络特性。神经网络结构的选择似乎常常是手工调整的,结果是有噪音的,而且与平台有关,但有时可以用代码来重现结果。最真实的例子来自工程和模拟,但在这些情况下,很少有再现高保真模拟的管道。除了表1中的情况外,例子还包括机翼、翅膀或风扇的设计[Chen et al. 2020a; Gaudrie et al. 2020; Lukaczyk et al. 2014; Palar and Shimoyama 2017; Seshadrietal. 2019;Viswanath等人,2011],汽车工业测试案例[Binois 2015],合金设计[Li等人,2017;Ranaetal.2017],生物学[Ulmasov等人,2016],物理学[Kirschner等人,2019;Mutny和Krause 2018],以及电子产品[Jones等人,1998]。
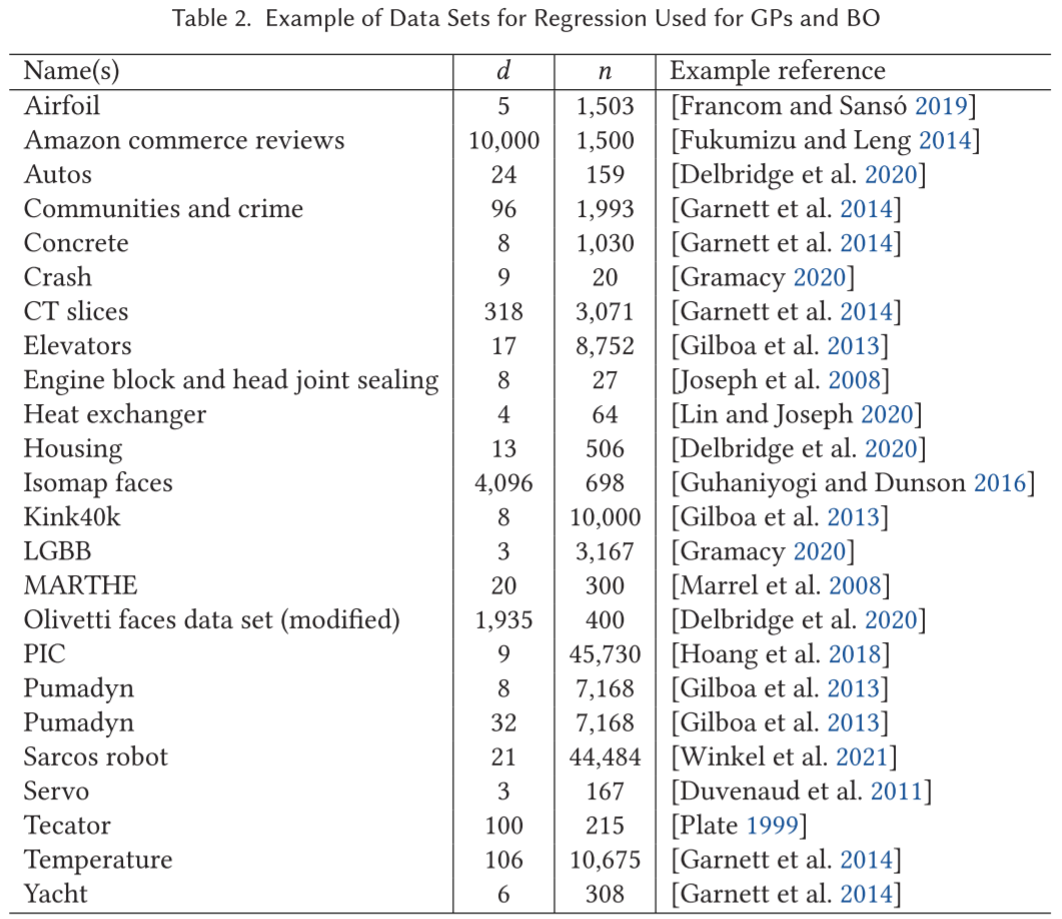
高维数据集是测试高维GP回归的另一个适当的选择,可以通过允许BO算法在输入空间中不选择任意的点,而只选择那些与观察数据相对应的点来扩展到BO。然而,这降低了获取函数的连续优化的效果,获取函数是真实黑盒上Bo的一个完全不可忽略的组成部分。尽管如此,表2中列出了一些已使用的回归任务的常见数据集。按照Jones[2008]在MOPTA会议上的例子,一种选择是对给定的数据集拟合一个插值,然后将该插值作为黑箱进行优化。我们应该指出,如果用于生成 "黑箱 "的插值与用于BO的插值相同,结果可能是不切实际的美好。
从上面列出的一组示例中,我们可以看到BO中 “高维” 的定义差异很大,从低到几千。优化预算具有相同的变化范围,但每个分析只针对一个固定的预算进行。因此,对于哪种高维结构在给定的维度和预算下是最适应的,或者甚至更好的是,随着更多的评估结果的出现,使更多的复杂性成为可能,这一点还有深入研究的空间。
6 结论和观点
高维度常常被正确地认为是基于GP的BO的首要挑战之一,已经产生了许多不同的想法来解决维度诅咒的每个方面的表现。虽然结构性假设似乎集中在变量选择、加法分解或线性嵌入中的一种或多种,但在解决该问题的最佳方式上没有达成共识。即使这在很大程度上是一个取决于问题的问题,但所使用的推理方法也限制了哪些结构是可能被假设的,无论是依靠随机结构还是实际尝试推断结构。即使除了这些具体细节,用于获取函数优化的特定策略也会使其他方面黯然失色。更加系统的比较是必要的,正如对合适的基准的定义一样。
6.1 一些一般准则
如第 3 节开头所述,大多数结构模型假设可以看作是更一般模型的实例:
m
o
d
e
l
:
f
(
x
)
≈
∑
i
=
1
K
g
i
(
A
i
x
)
(10)
model:\ f(\mathbf{x}) \approx \sum\limits_{i=1}^{\mathcal K}g_i(\mathbf{A_ix}) \tag {10}
model: f(x)≈i=1∑Kgi(Aix)(10)
其中
A
i
∈
R
r
×
d
,
K
∈
N
∗
\mathbf A_i ∈ \mathbb R^{r×d}, \mathcal K ∈ \mathbb N^∗
Ai∈Rr×d,K∈N∗,它允许低维效应的总和。这包括Durrande等人[2012]的加性高斯过程,它将每个变量单独分离到它自己的bin中,在另一端是
f
(
x
)
=
h
(
A
x
)
f(\mathbf x)=h(\mathbf {Ax})
f(x)=h(Ax) 形式的线性嵌入,它忽略了某些输入方向,此外还有Muehlenstaedt等人[2012]的功能方差核,或结合几个随机低维子空间,如Delbridge等人。在这些方法的交叉点上仍有很好的研究方向,我们特别认为,"默认 "的核成分,例如简单的各向同性核,可以对搜索输入空间特定部分的方法起到补充作用。这些不同的结构模型选择已经在分类学中被总结出来,图1,以及它们的联系。
我们建议不要直接从最一般的模型开始,因为它的直接推断会做出非常陡峭的初始步骤,我们建议首先尝试更简单的模型。也就是说,从标准GP开始,基于ARD原理构建替代GP,或者计算像Sobol指数这样的灵敏度指数。然后构建一个完全可加的 GP 模型或单索引模型作为加法和线性嵌入系列的基本模型。通过比较这些简单模型给出的预测,可以从性能最好的模型构建更高级的模型:功能 ANOVA 或从添加剂模型中的块添加剂;在单个索引之上的线性嵌入。 Ifnone 表现良好,则可以考虑投影追踪或非线性嵌入,如果 n 足够大以允许对相应模型进行可靠推断。更准确地说,对于推断,取决于 d d d,预算 n n n 和 f f f 的与应用相关的复杂性,最好采用最大似然 (或者更好的是贝叶斯替代方案) 进行推断。如果当 d d d 达到数百时太难或太慢,那么依靠随机结构绕过全维模型推断仍然是可能的。最简单的模型随着 d d d 的增加在计算上有很好的扩展,而更复杂的模型可能受益于最近越来越多的使用GPU和自动微分框架带来的进步。这一点尤其正确,因为更复杂的模型需要更大的 n n n 值来显示改进。
另外,如果优化的预算有限,对 "不活跃 "的变量采取简单的填充策略,并在一些受限的子空间上进行优化,可能是更好的选择。最后,信任区框架的使用在高维问题的优化方面显示出有希望的结果,并且适合于并行化。
6.2 未来展望
模型、推理方法和数学优化技术之间存在着混合的潜力。对于全局优化,Spagnol等人[2019]指出的一个研究途径是关注那些对达到低函数值很重要的变量,而不是评估它们对整个f范围的影响。[2020b]在某种程度上专注于低值,正如Guhaniyogi和Dunson[2016]对流形约束输入的评价。怀疑当前结构假设的能力也可能相当有助于避免适应性设计中出现的负反馈循环效应,见,例如,Gramacy [2020]。
将内核定义在整个初始域上的能力是否优于直接在低维嵌入上定义内核(这虽然有吸引力,但与领域选择问题有关),还有待观察。如果定义在嵌入上的核确实是首选,那么通过增加一个各向同性的成分来保持核有足够的表现力(例如,不像Durrande等人[2013]那样被限制为一阶加性),可以通过考虑正交加性[Ginsbourger等人2016]而得到改善。这些正交性约束可能会通过减少可识别性问题来帮助推理。
此外,将搜索空间限制在输入空间的某个子集的信任区域BO方法的成功,促使了本身是局部的降维方法。例如,Wycoff [2021a] 建议针对具有非均匀密度的概率度量定义一个活动子空间,以强调某些感兴趣的区域。即,焦点限于信赖域,但是可以考虑其他方案。当然,局部线性的降维实际上是全局非线性的,并且这样的局部线性模型可以被证明是开发BO的非线性降维的易处理的方法。
此外,由于数学编程对高维贝叶斯优化方法的影响,已经产生了有用的结果。特别是,在Eriksson等人 [2019] 中使用矩形信任区域似乎是有益的,并且在Gramacy等人 [2016] 和Picheny等人 [2016] 中开发了增广拉格朗日方法的高斯过程类似物。帮助开发新算法,将低维建模的好处与信任区域或其他在高维数学编程中成功的方法相结合,可以帮助BO最终在复杂的高维问题上实现实用,广泛使用的飞跃。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








